我觉得这或许是因为当时的证据并不见得像现在很多人认为的那样完备且令人信服,如“麦哲伦环球航行就可以证明地圆”的论证实际上也是有欠缺的[1],对地球形态的认知发展其实也有很长的历程与变化。
在现代确论以前,古人通行过众多的世界观,而且很多世界观并不一定表述的是“整个世界的形体”。
尽管这些观点与我们的不同,而且大多数都被证明是错误的,但秉持这些观点的人们一般都有足够的理由来这么做。[2]
当然,我并不是要说持“地半球”“地平”之流的世界观,就更加完备了;同期横向对比,近世以前的学说们所持的证据都是有限的,没法全球测量的情况下,大家都非常不完备。
可不完备,也不影响不同的世界观各有长处,存在各不相同又一定程度上契合今人认知的表述。
未丈量全球,何能实证地体的球形?
在没法去往全球实测,拿不到完备证据的情况下,大家求解不唯一,“平”“球”并不是唯二备选,半球说和其他解释也何其繁多;哪怕都支持地球是球,也会有不一样的见解,甚至互相攻讦,到 18 世纪,仍有争地球到底是个“立着的长西瓜”(两极更长)还是牛顿提出的扁球形状的学术大论战[3],大家手里证据在那时都还不完善。
现代人能知道地球是近似球形的不规则椭球体这样较为完备的结论,依赖的很多证据直到近世[4]才被发现。
在此之前的很多能“证明地圆的证据”实际上只能证明局部并不平整[5]或者部分方向存在曲率[6],推广到证明地球还需要更多支撑,如在全球多地不断去测量求证;可因为证明者已经支持地球论,所以哪怕只掌握少量证据或者存疑证据,他们也会理直气壮地拿来证明地球只能是球形。很多论述中间推演过程能“符合逻辑”,但这同样不影响立论者干射箭画靶的事情不总是合理,很多论证的出发点今人会觉得非常荒谬。
曲率被察觉,据说非常早,可虽认可大地不平,但大地为何不能是柱状和其他状?毕竟那时也无人能超脱地球,去观察整个地球的全貌直接“认识”整个地球形体,大家拿到的也只是一些零散的旁证。“这些证据在球假设下成立”和“存在可以实现如此证据的其他假设”不存在不言自明的“矛盾”。

一些版本的论述中,据称在出没星这一证据下,古希腊先哲阿那克西曼德发现了天地并不平直的问题,最早提出了完整天球的设想[7],但他支持大地总体是个柱子[8],哪怕这个假设将涉及非常多其没见过的地方,甚至已知之外的土地在这种假设中才是构成假想的大地的大多数。
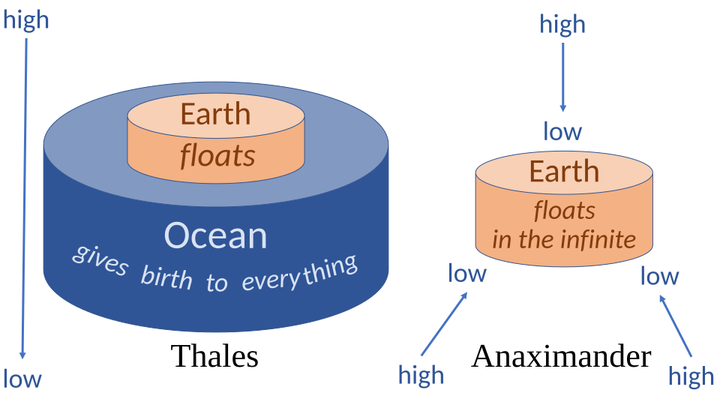
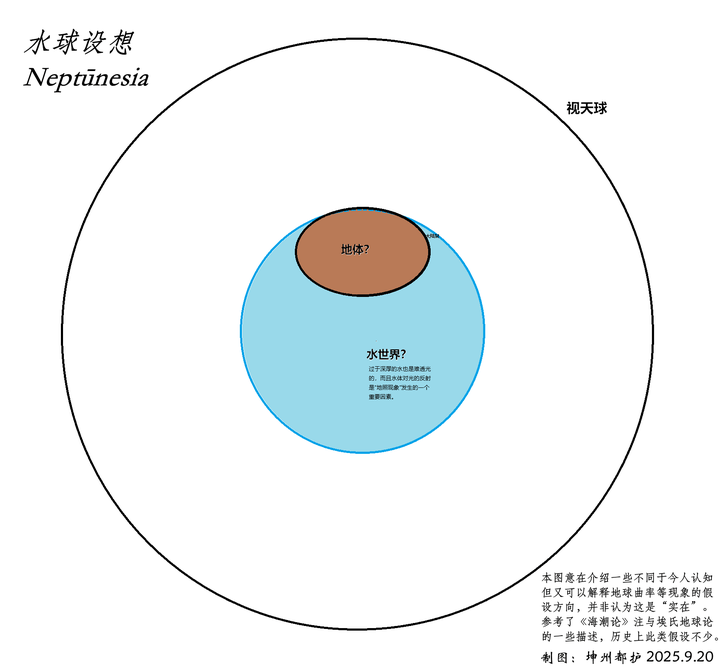
甚至,从何时开始,现代语境的“地”(Geo/Terra/Earth)已经是“不言自明”就包括整个“我们脚下的整个球形世界”(World/Orbis/Globe)了呢?若地只是一个大水球当中所悬浮的一小部分,不也可以吗?今人能知道海面下都是坚实的地壳也是通过巨量的观察和实证而确认的,可这对古人不是不言自明的。
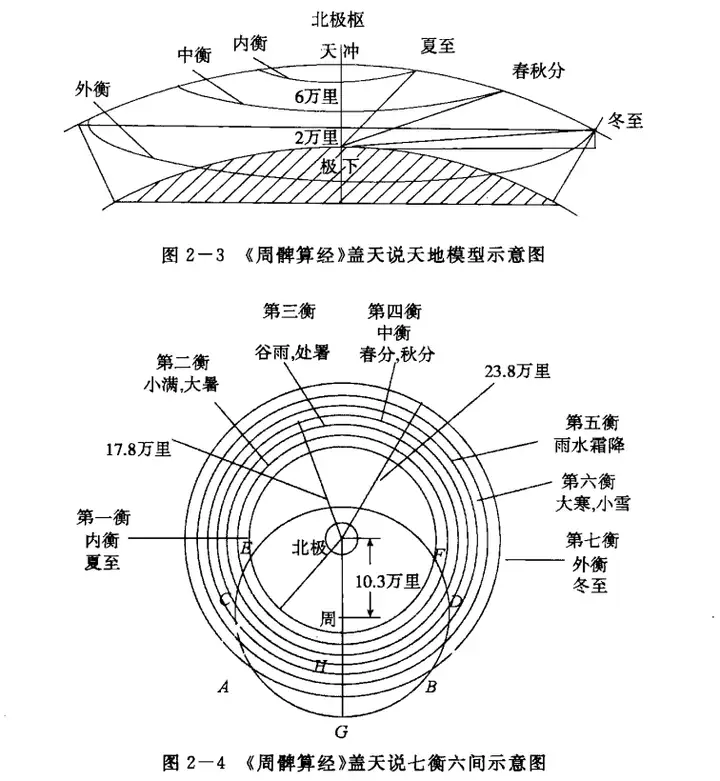
反观《周髀》建立的模型,就只是假设天地间“已知”局部,其描述大地和天空可知部分呈弧形,而局部之外直言承认不知[9]。固然这个模型当中已知部分的大小在今人看来也有一定的问题(这里一里多大也有争议),可不知为不知的态度才是我们应该提倡的。
不过进行大胆假设,亦不该苛责。古人拿不到较为全面的证据,更没有在全球进行大地测量,有各种各样不同的推测亦无可厚非[10],地球说并不总是在局限的证据下更完备,抑或是能很好地回答人们繁多而不同的认知疑问。
比对现代而言,缺乏测量证据的情况更是一直存在,虽自古累计有不少测量的努力,可很多大地测量的数据竟是自相矛盾的[11],更别说用来还原地球的形体了。
到了 18 世纪,定位测绘技术也得到了广泛发展,实测经度等[12]新技术也广泛冒出。越来越多的国家加入大地测量行列,甚至远在极东的大清都进行了很多庞大的精密测量工程[13],同时全球化在如火如荼进行着,世界交流更频繁了,大家能同时收集的全球的大地测量实测证据也自此越来越多,地球形体呈球状的结论才更加稳固。
不过稳固,并不代表结论已彻底完善,也不代表证明的完备[14]。
两百年后,人们终于能从太空查看地球甚至直接丈量地球,地球的球状形态最终无可争议地呈现在了大众的眼中[15]。
少量舆测可以实证球形?
题主提到了“古人用舆测距离,那么它得到的多个点的距离肯定是不平衡的”,认为这或许能是一个地球是圆的旁证,但一般舆测尺度下“不平衡”导致的差距可能还没测量误差大。
而且古今地图用途与制法不好一概论之,双方的标准很不一样。哪怕有计里画方,舆测与舆图记载的相对距离一般是路程而非“直线距离”。
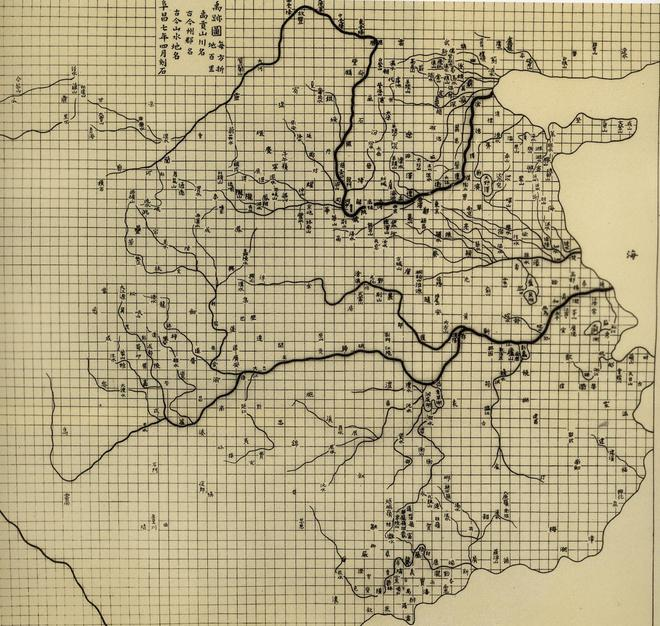
就算能测量非常精确的直线距离,同时也可以精确计算,这也只能证明测量点之间的大地范围不是平整的,反推到整个地球是近似圆形的曲面还差了恒河沙数的证据。
也有很多人认为埃拉托色尼的测量,是实证球形的一次杰出尝试。但这个实验是埃拉托色尼以世界整体是球形[16]为前提,据此来计算周长的,他人试图用测算结果证明测算的预设前提是不是搞错了什么。
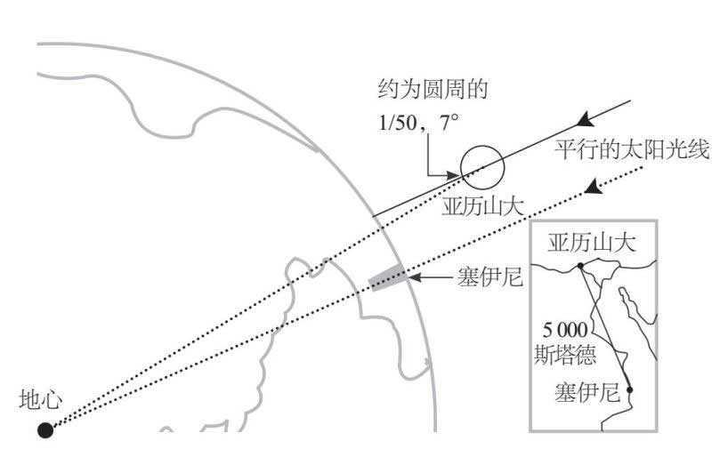
而且采集的数据只能证明两座城市面对太阳光的角度不一致,其甚至没有测中间的城市是否直射角度是规律变化的,用个别例子来实证全球曲率与周长更是……嗯,误差恰好抵消,他数据和现代值竟然挺接近。结果上来说真是人有多大胆,名有多大传……[17]
同时,埃氏认知的球,到底是否是“地球”也可疑[18]。虽然今人已知地球上被海洋覆盖的面积远比陆地大,不过今人还能够知道海面下都是坚实的地壳,故我们称“世界”为“地球”是可行的;但古人没有这样的观测,也无法进行论证。
有限的观测证据能否推广到整个”世界“是令人怀疑的,虽周长结果相近,但这不代表如此假定合理;到了后世,我们知道了地球并非正圆,曲率各地有不同的微小变化,不对全球各地都进行实测,我们很难说明个例与整体特性是否相关,更难直接得出“真论”了。对地体的形状实证还是需要更多实测,而受限于时代,环球尺度的测值很难收集得足够。
对地球形态认知的发展
让我们来重新审视一下地球是球形的结论的得出。
很多人认为麦哲伦的航行实证地球,但“环球航行”实际上在地盘和圆柱模型当中其实都能找到解,且在麦哲伦航行之前,先验的“地球是个球”的观点,已经广泛被西欧的受教育群体人接受了[19],实际上单一的全球航行行为,对证明地球是球既不充分也不必要。

虽然相关的理论学说,在科学史发展上看上去像是一脉相承的,是“线性发展”的,但实际上人类对地球认知的过程还是有些曲折的;虽古今人说的世界观都是“地球论”,但我们今天所认识的“地球常识”并不是一开始就是那样的,古人先射出的箭,站对了假说方向,并不意味着他们的论证基础就不存在问题了。
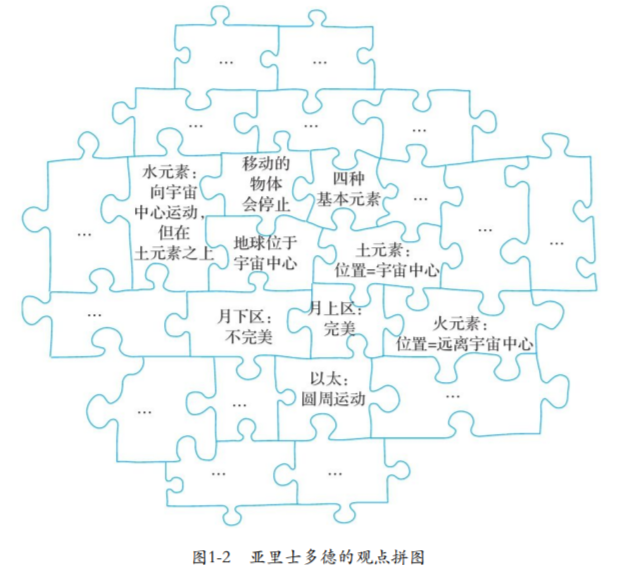
要特别注意的是,今天被称为“地球说”的体系,并不只需要解释地球形体与交食,时人也需要回答很多现代人或觉得很莫名其妙的问题,从出现到漫长的发展历程,无数代人也为此不断增加假设“实体”(如为了"拯救现象"的哲学要求,保留“完美的圆”,亚氏理论使用了实体同心球[20])。这一整个体系当中的假设是互相支撑的,而不能单单把“球形”观点割裂开来单独看待[21]。
从天球回到大地——地球说的提出
要回顾地球概念的提出,我们可能得先看向天球,不过由于时间过于久远,这些历史很难溯源到争议较少的出处,我所梳理也不一定不存在问题。
据 Britannica 所述,前文米利都学派的阿纳克西曼德,可能是天球的独立发明者之一;由天体视运动的表现把天看成弧面是比较常见的,而阿纳克西曼德在此更进一步,提出了无限的世界和有限的大地,其认为“无限”的天则显然成完美正球形,有限的大地居于其中。
天球已出现,推广到地也不是什么难想的事情,从一些后人作品可以看出,阿纳克西曼德的无限空间思想给后来的毕达哥拉斯学派球形天地提供了一定的基础。
接力就这么来到了毕达哥拉斯学派,他们认为“在所有平面的形状中,圆形是最完美的,而在所有的立体形状中,球形是最完美的,所以我们生活的世界应当是球形”,这一论证同时对天球和地球进行了推广。
显而易见,地球说在此处被提出时是相当“先验”的,一般也认为开始时他们并无什么证据。
先验的地球说已然存在,所以就有了很多人跟着往这些方向立论,同时也会带动后人去给其找证据,如出没星与恒显星的南北方向观测变化、地球影子之类的证据[22],被后世作为了“正球”是不言自明之唯一解的证据;部分只能证明地球局地或者局部方向曲率存在的证据,被扩大到“实证地球是精确的正球”,甚至一些后世支持者会据少量论证就开始表述其他解不存在[23]。
天文学已大成?——早期的成熟球说
或成书于 2 世纪托勒玫的《至大论》的世界观体系,大概算是球说的一个重要阶段性成果。
很多新证据[24]和理论被托氏用在证明人居世界是球形上[25],一些球面上的三角几何理论也开始出现;但就像最前面论述的,这时对整个体系的证明也不会是完全完备的,对球状形体的描述也停留在“完美球形”一级。
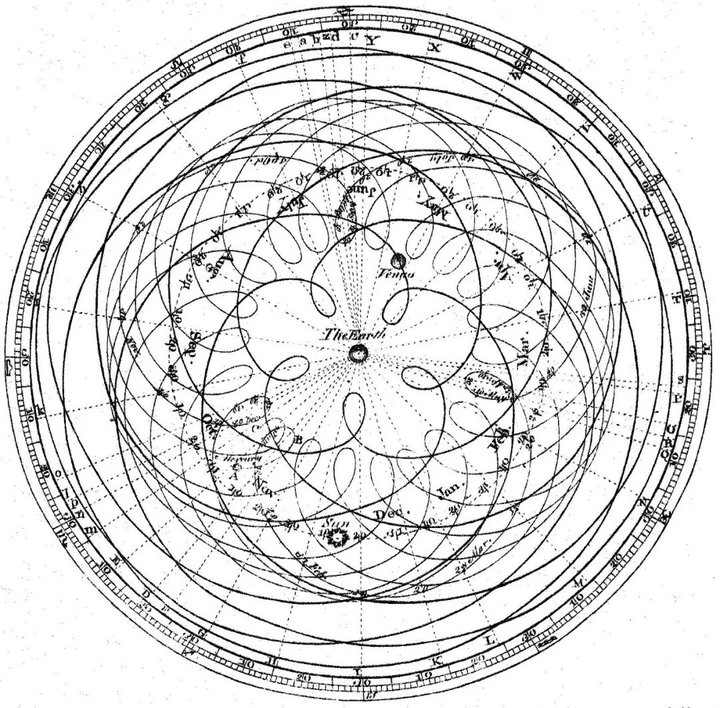
虽然作为实体的同心球假设被放弃了,但“完美正圆”思想和“拯救现象”路径仍然保留着[20],托勒玫的地心体系在描述天体运行时,使用了本轮嵌套均轮这样的天才方法。
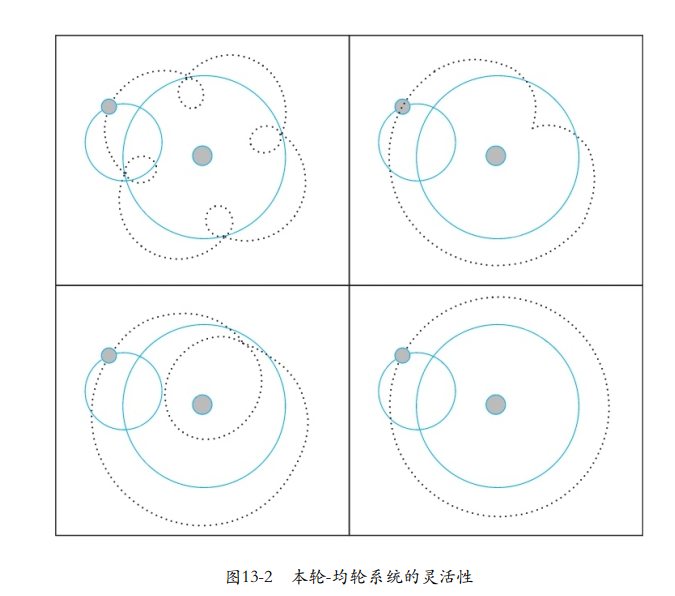
这样的方法一直沿用了千余年,哪怕到 16 世纪后,哥白尼自己仍然在使用构造本轮和均轮的方法,甚至他捡起了早被一定程度扬弃的实体天球假设[26]。
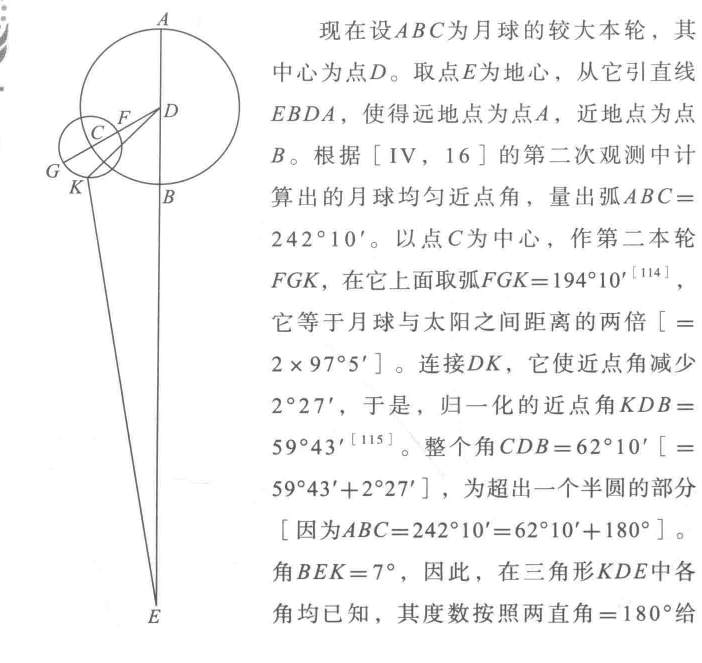
不过虽不完备,在这套成熟球说的认知指导下,才有了 15-16 世纪之交哥伦布的向西航行与麦哲伦的全球航行。麦哲伦的这个航行,更多是直接证明了世界各大洋是联通的,告诉了欧洲人向西真的可以去中国和印度!这一行为对全球化和大航海贡献颇多。
正圆已否!——地椭球说
到了 17 世纪,随着哥白尼革命的进行,构造本轮和均轮的方法最终被新的学说取代;后继者开普勒,用椭圆轨道理论取代了前述方法。
既然不存在完美的正圆轨道或实体天球,那么地球会不会也不是正球体?
随着日心说和地球自转愈发被大家所认可,牛顿在 17 世纪末也对此进行了深入研究,论证了地球自转对地球形态的影响,认为地球应是一个赤道略为隆起、两极略为扁平的椭球体。
牛顿的学说并未直接折服所有人,这个椭球是赤道宽还是两极宽法国和英国学者们有不同的意见,争议长达数十年,当时的人们虽然也有测量地球的形状,但是很多测量结果甚至是自相矛盾的。
18 世纪初,卡西尼一世等的有局限的测量反而得出了两极更长的结果(与今论相反)。这个测量结果被笛卡尔力学的支持者拿来作为论据,反对牛顿的力学学说对地球形体的解释,乃至反对牛顿的整套体系[3]。
测量还在继续,1730s 法国官方派遣了新的探遣队前往了南半球与北极附近,试图彻底解决争议;在 1740s,法国科学院的新实测数据公布,人们终于可以下地球呈两极稍扁的近椭球体形状的结论[13],英方所持的来自牛顿的观点,更加贴合地球实际。
至 1743 年,参与上文“新实测”的法国学者克莱洛,指出了牛顿计算存在的问题,提出了新的算法(克莱洛定理,给出了地球几何扁率与重力扁率的数学关系)。其模型认为地球的外表面应是一个水准椭球,即椭球表面上各点的重力位相等。理论很精致,但后来我们知道了,真实结果并不如数学模型那样简单。
复杂而不规整的现实——大地水准面
时间仍在流逝,人们对大地形体的测量实践也仍在继续。各地的测量越来越多,大地测量数据也大为丰富,地球是个近似的球体的证据更加充分。不过随着技术的进步,测量的精度也越来越大,此前的椭球说,也无法满足测量的需要了。
到了 19 世纪,人们也开始发现地球的形态和重力分布也不是那么规整(要注意的是,这个不规整是小尺度的,网上有很多夸张化水准面的“地球形状图”,地球还总是比大多数乒乓球更圆的)。
在 1828 年,德国的高斯提出了与全球平均海面最为接近的重力等位面;到1873 年,高斯的学生利斯廷创造出了大地水准面一词,以描述高斯提出的数学表面,就此大地测量理论迈向了一个新的高度。
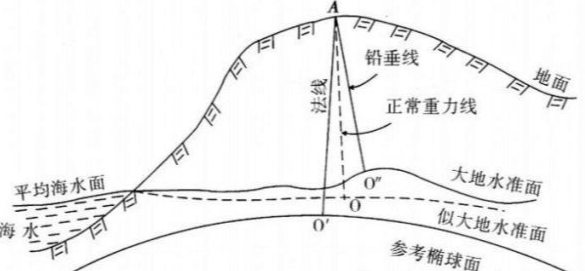
此后的两百年里,新的测量方法也一直在改进,我国在二十多年前也用地球重力场逼近理论确定出了中国 2000 似大地水准面(CQG2000),在可见的未来,相关的研究也会继续推进下去[27]。
某种意义上讲,题主提到的“测量不平衡而认知圆形”这一设想所提到的实践方向确实理论上可行;但世界终究是复杂的,这一实践路径反而导向了“测量让人们发现地球并非正球”的实践结果,这不是非常有意思吗?
余论
虽然,地球说的历史被追溯的很长,且有一些“很有说服力的证据”在古今都被使用来说明地球是球形,同时古今的“地球说”看上去有不少相似地方,但相似终归还是不可同日而语。
我们应当注意到,对地球是球的证明,很长一段时间其实是非常不完备的,解并不唯一,哪怕到 18 世纪,英法也还在为两极和赤道哪个为椭球长轴争论;历经两千多年的发展,证据越来越多,学说才比较完备,到上个世纪,地球的照片也被人类所拍摄了,我们才可以非常简单地用单一的证据说“地球呈球形”是证据完备的。
所以此前的人们不直接相信地球是圆的,其实一般都有足够的理由来这么做。[28]
不过另一方面来讲,中国古人其实并不是没人认知到相关问题,甚至有人为球形大地上人怎么生存进行了简要论述:
姑射谪女曰:天上地下而人在中,何义?九天先生曰:谓天外地内则可,谓天上地下则不可。天地人物不犹鸡卵乎?天为卵壳,地为卵黄,人物为卵白。[29]
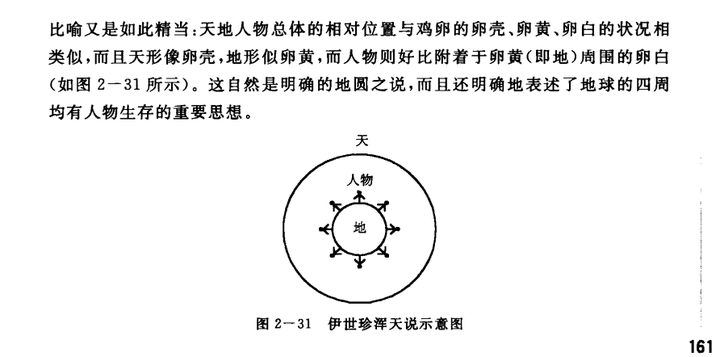
自先秦以降,对大地平坦的质疑乃至直接提出大地是不平[30]的观点相关记载,其实还是能找到很多的,多找找的话提到地球的记载也不少。第一节当中所绘制的“水球”的解法,参考的假设也是来自中国古人。不过本文这里限于篇幅,我就不再继续展开了,我之前回答所作长文提到了一些相关证据,不过大部分记载立说和现代地球论也基本大相径庭。
总的来说,我觉得题主的想法还是很有意思的,故作此回答;当然,我也想谈这类问题很久了,感谢题主提供了一个很好的舞台,也希望大家可以多多支持,也欢迎大家前来交流探讨。
现在收到了很多反馈意见,修修改改几天,本文也近六千字了,虽然我继续展开了一些内容,但还是有很多涉及到的知识限于篇幅难以展开,论述也可能有我不自觉跳跃的地方。大家可以参考注释当中提到的文献进行拓展阅读。最后的最后,我在这也谢谢大家的支持。
