其实，太阳功率密度非常低，仅仅只有 0.0018W/kg。而人体为 1.5~2W/kg，是太阳的 1000 倍。

太阳每秒钟消耗的质量，更为精确的值是 428 万吨。

由于是核反应，可直接通过质能守恒换算。

求得每秒钟，太阳释放的热量为：

3.85×10^26 J

这个能量的确极其的庞大。

大家可能对指数没有什么概念，我们不妨对比一下。

太阳的总能量大约只有 22 亿分之一会照射到地球上，地球接受的每秒钟热辐量为：

1.74×10^17 J。

这个数据其实依旧非常庞大。

因为人类文明当前 1 秒钟总做功的 2 x 10^13 J。

这又是地球接受太阳热辐射的近万分之一。

也就是说，人类文明的总功率，仅仅只有太阳功率的近 20 万亿分之一。

依据卡尔达舍夫文明等级^[1]：

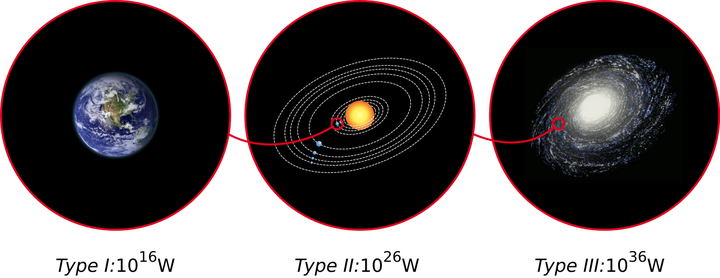
能达到行星表面总功率的文明是一级文明（10^16W），能够达到整个恒星总功率的是 2 级文明（10^26W），能达到整个星系总功率的是 3 级文明（10^36W）。

计算公式为：

从这个公式我们可以计算出，对于 2 x 10^13 W 的当前人类。

文明等级为：0.73

虽然太阳的功率很高，但功率密度却很低。

太阳重达 1.99×10^30 kg，相当于人类总质量的 400 亿亿倍。

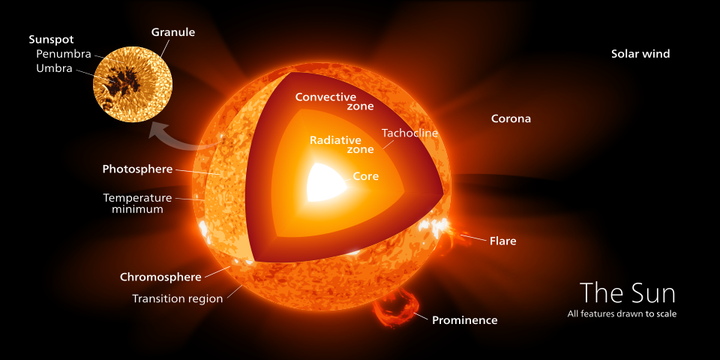
太阳热量的产生，主要来源于内核。

其内核温度 1570 万 K，但依旧达不到经典的氢 - 氢聚变的温度。

我们不妨先算一下，需要多高的温度。

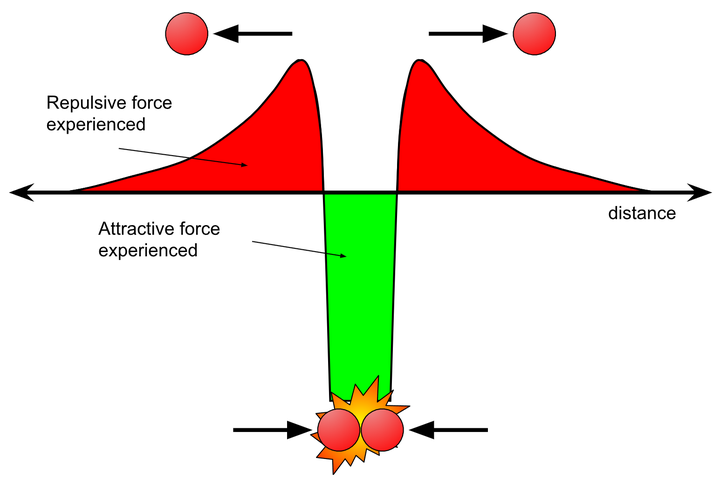
质子之间在较远距离，因相同电荷，在电磁作用下相互排斥。

随着靠的越近，排斥力也越大（下图红色部分）。

然而当突破势垒后，强相互作用的吸引力占主导（绿色），而发生核聚变（质子 - 质子链反应）。

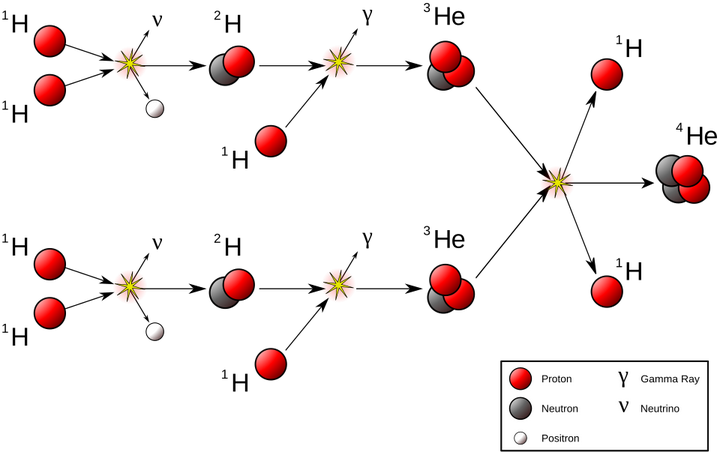
质子所需的能量，等于将质子从某个位置移动到另一个位置所做功的数值。

依据玻尔兹曼分布，每个粒子的平均能量与温度的关系为。

那么，

求得：

T≈3×10^9 K

也即，在不考虑其它因素的条件下，经典氢氢聚变的最低温度便高达 30 亿℃。

这个温度，相当于太阳内核温度的 200 倍。

虽然太阳内核压强高达 2500 亿个大气压，密度达到 150000kg/m^3。但温度达不到经典聚变的条件，所以完全不会发生经典聚变。

其实，如果是在人类低密度的聚变模拟装置中，实际超过 100 亿℃，都难以达到理想的聚变效率。

这是人类聚变模拟装置中，三种核物质不同混合下，聚变反应的温度与速率关系。

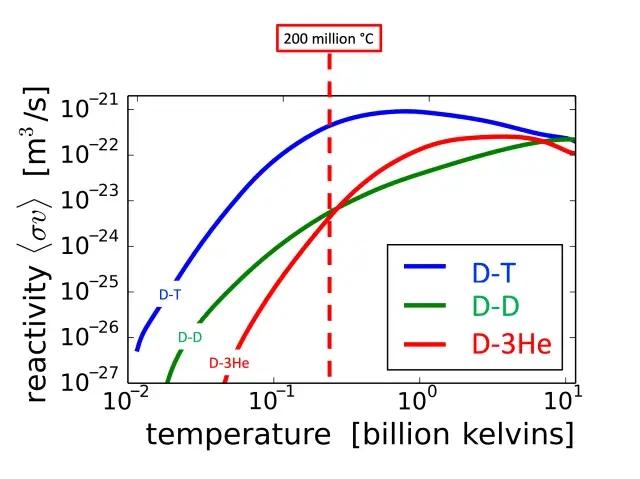
氘氚（D-T）大约在 1000 万℃就会开始反应，氘氘（D-D）需要 2000 万℃，氘氦 3（D-3He）需要 5000 万℃。

虽然超过 2000 万℃，氘氘和氘氚聚变都足以发生，但温度太低时反应速率过低。一般认为，1 亿℃以上是氘氚反应堆可行的最低温度。而氘氦 3 需要 10 亿℃，氘氘更是需要 100 亿℃。

氢氢反应堆条件，更是远远超过 100 亿℃。

基本可以认为，除非恒星内核条件，氢氢聚变不可能发生。

既然太阳无法发生经典氢氢聚变，那它又是如何聚变“燃烧”的呢？

因为高压强和高致密度，让另外一个非经典的低概率聚变，变得突出了起来。

那就是量子隧穿聚变。

虽然在经典条件下，两颗质子无法直接突破电磁势垒而发生聚变。

但量子效应的随机性，却使得质子有概率直接隧穿电磁势垒，而发生核聚变。

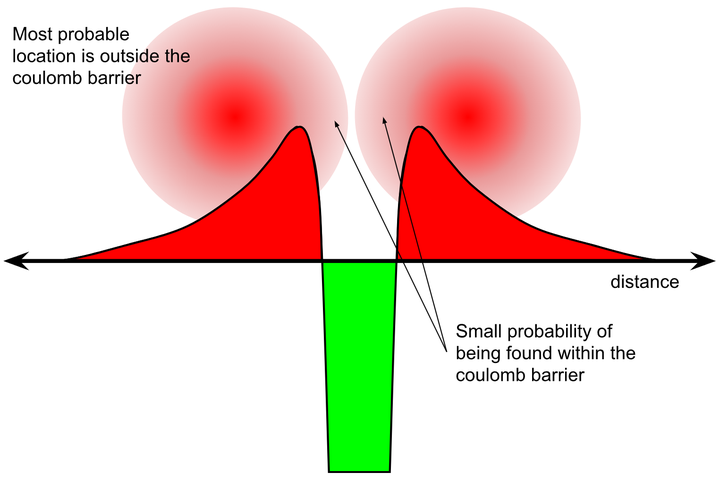
不过质子量子隧穿聚变的概率非常低。

低至 1/10^28，也即 1 万亿亿亿分之一。

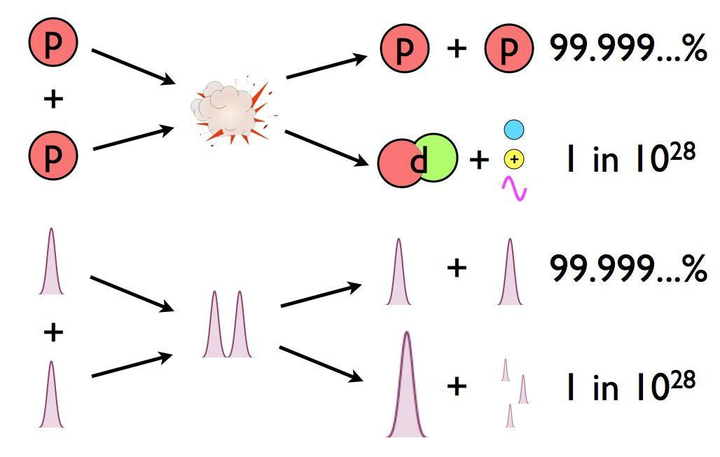
在常规条件下，由于概率非常低，甚至可以约等于不会发生。

但太阳内核就不同了。

自由质子的密度极高，达到 3×10^31 个 /m^3。

相当于人造太阳（10^20）的 3 千亿倍。

如此高的致密度，可以大大增加量子隧穿的反应率。

太阳的总自由质数达到 8.9×10^56 个，使得它每秒钟发生质子 - 质子链的次数高达 9.2×10^37 次。

虽然这个数据很庞大……

但整体低概率的量子隧穿聚变，就注定了相比起经典核聚变，依旧是一个效率非常低的聚变。

平均每个质子大约需要 90 亿年的时间，才能完成质子 - 质子链聚变过程。

这也就使得，虽然太阳的总功率极高，但功率密度却非常低。

太阳核心的功率密度为 276.5W/m^3。

通过 150000kg/m^3 的密度，换算成质量比，仅仅只有 0.0018W/kg。

而人体功率是多少呢？

不放一算。

这是人体在不同状态下的新陈代谢率^[2]：

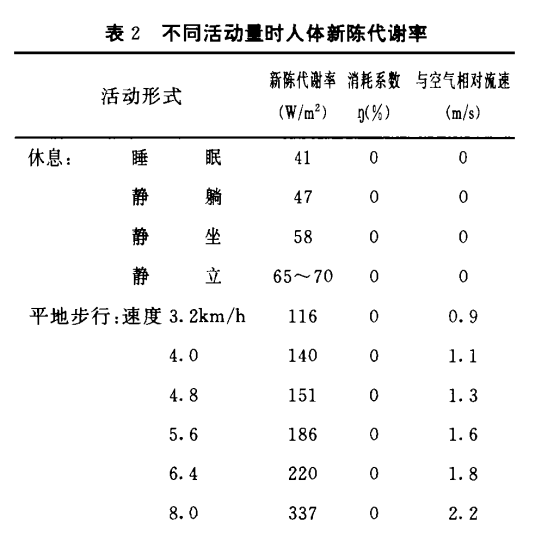
• 新陈代谢率 × 人体面积 = 人体热功率

人一天大约 1/3 的时间睡觉，1/3 的时间静坐，剩下 1/3 主要为静立到行走不等，不妨以低速步行为准。

那么人体一天平均新陈代谢率为：

（41+58+116）/3=71.67W/m^2。

皮肤表面积可由许文生氏公式得到，也即：

• 体表面积（m2）=0.0061×身高（cm）+0.0128×体重（kg）-0.1529。

全年龄的全球成年男性平均身高为 171 厘米，女性为 159 厘米。上下限，为 1.4~2 米。

求得，男女体表面积的主要区间为：

1.2~2m^2。

我们取个 1.6m^2 的平均值。

那么，人体平均功率为：

114.67W

也即，人体平均功率大约在 100W 左右，极其不爱动的小巧女生，可显著低于 100W。

求得人体平均功率密度为：1.5~2W/kg，平均 1.75W/kg。

那么单位质量下，人体的功率密度约为太阳的 1000 倍。

太阳功率密度如此之低，也就决定了它正常寿命可以超过 100 亿年的时间。

如果不是晚年“燃烧”（壳层聚变）速度会加快，它的寿命还会增加至少 2 倍以上的时间。

其实太阳一生消耗的氢，大约只有 60%左右。

如果完全只按照主序星阶段的聚变速率，假设所有的氢都能聚变，需要的时间是 732 亿年。

732 亿年比起 46 亿年，更是久多了。