省流:
喝一口相当于喝了
口,那葫芦的饮用期望即为
直接计算的话,可以得到数学期望为:
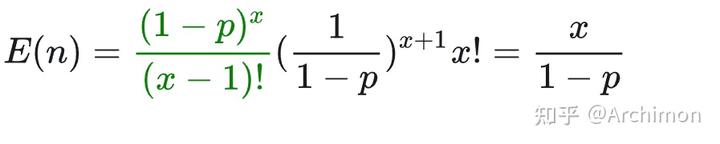
在针对满级的『上清宝葫芦』一万次模拟中,有三只『天命吗喽』一葫芦喝了 20 口酒,相当于额外背了个葫芦;另外有 2012 只普通猴子只喝到了原本的 10 口酒,可谓是泡了等于白泡。
饮用期望
饮用期望的计算有两种方式,一种是便于计算的反向考虑,一种是便于考虑的直接计算:
反向考虑
有
的概率不消耗葫芦的使用次数,那就是有
的概率会消耗葫芦的使用次数,也是每喝一口消耗的使用次数期望为『
次』,那葫芦的饮用期望即为
直接计算
直接计算饮用次数的期望的话,我们首先要计算第
次喝完的概率
。为了叙述方便,这里我们称不消耗次数的饮酒为『奖励事件』,发生概率为
;消耗次数的情况为普通事件,发生概率为
;为了推导过程的美观,葫芦总容量用字母
表示
『第
次喝完』意味着事件
『第
次事件为普通事件』和事件
『前
次发生了
次奖励事件』同时发生。事件
的发生概率为
,事件
的发生概率可以表示为
由于事件
相互独立,则:
那么,饮用次数的期望即为:
我们可以看到,在上式中绿色的部分实际上是一个与
无关的常量,所以我们将其提出求和进行简化。现在我们考虑求和内部的内容,做以下代换。
观察上式右侧结果,实际上相当于是
对
求了
次导,所以我们可以进一步得到:
从而期望为:
模拟验证
我们也可以做一个简单的模拟进行验证。以『上清宝葫芦』为例,升到满级后总共可以喝 10 口,蜂山石髓有 15%的概率不消耗使用次数,那么按照上式计算出的使用期望约为11.76.

我们可以用以下方式进行 10000 次模拟:
from random import randint
def hulu_whole():
left_drinks = 10
drink_times = 0
while left_drinks > 0:
drink_times += 1
if randint(1,100) < 86:
left_drinks -= 1
else:
# 触发蜂山石髓,不消耗次数
pass
return drink_times
test_10000 = []
for i in range(10000):
test_10000.append(hulu_whole())
如代码所示,每次模拟都到喝光葫芦停止,记录最终喝的次数。
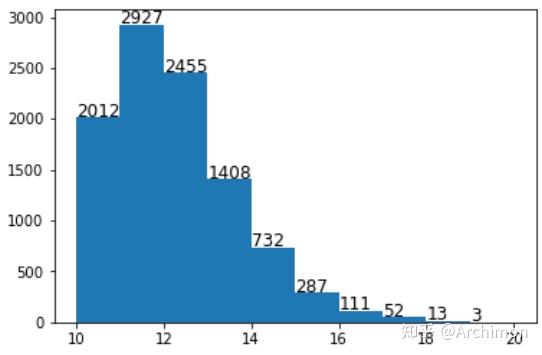
最终结果如上图所示:在这一万次的模拟中,有三只『天命吗喽』一葫芦喝了 20 口酒,相当于额外背了个葫芦;另外有 2012 只普通猴子只喝到了原本的 10 口酒,可谓是泡了等于白泡。
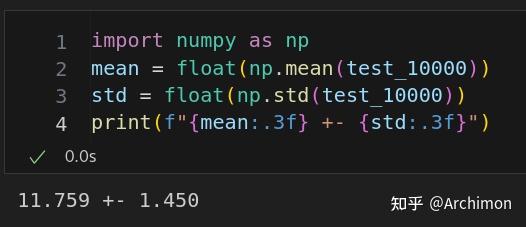
平均下来,每个葫芦提供了 11.759 口酒,和我们计算的结果相吻合。
大家如果对于游戏中的数学感兴趣的话,还可以看看这个回答:
