数学中有哪些巧合让人眼前一亮？

温尊，知不可乎骤得，托遗响于悲风。

小时候，知道一次函数是一根直线，二次函数是抛物线，于是我就想知道三次函数，四次函数是什么样的呢？当时的我选择百度一下图片(当然图片是我刚刚百度的)：

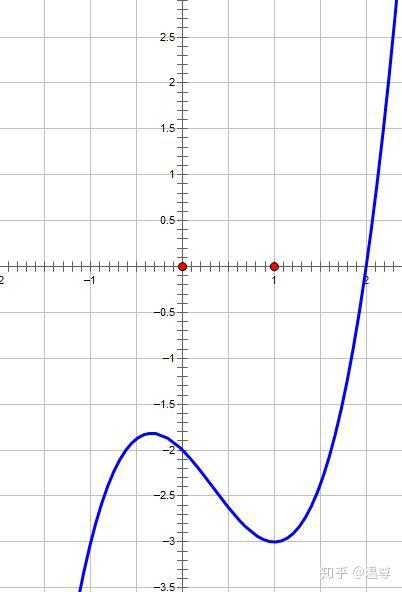
哇这三次函数"勾"了两次！再看看四次函数吧：

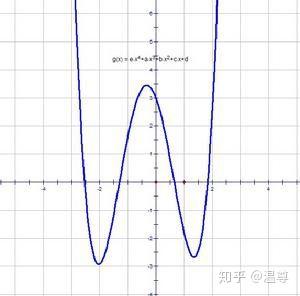
哇勾了三次，是不是

$n$

次函数就要"勾"

$n-1$

次呢？

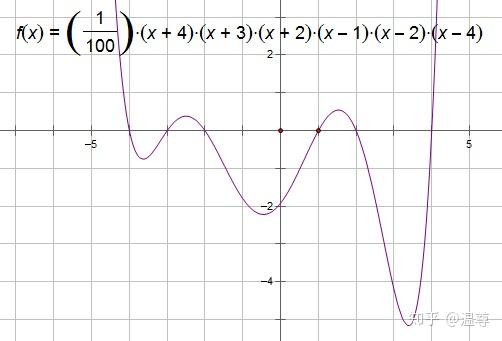
哇这六次函数不就"勾"了五次吗？于是感觉发现了新天地.

后来发现关联栏里面有一个叫三角函数的东西，于是点击，查看：

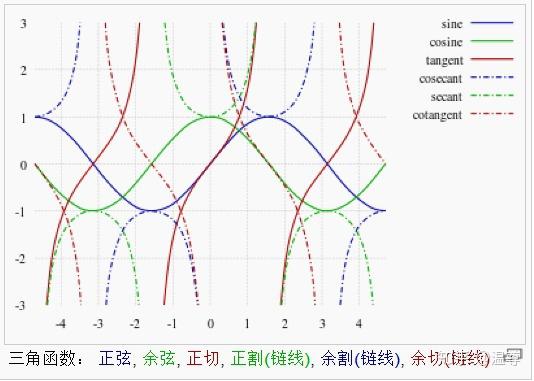
卧槽，这不就是"勾"了无数次的一个

$\infty$

次函数吗？于是我选择直接百度“函数”的图片：

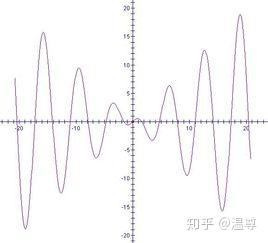
我就想，是不是所有平滑曲线函数都可以用一个

$\infty$

次函数代替呢？

后来初中末期时候，因为酷爱数学，所以自学一些东西，才知道了结果，就是大名鼎鼎的

$Taylor$

展开(

$Peano$

余项).

【Th】设函数

$f:[a,b]\rightarrow\mathbb{C}$

在

$a$

处

$n$

阶可导，则当

$x\rightarrow a^{+}$

时，有：

$f(x)=f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+...+\frac{f^{(n)}(a)}{n!}(x-a)^n+o((x-a)^n).$

事实上可以写成

$Taylor$

级数

$f(x)=\sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n.$

这果然是一个

$\infty$

次函数嘛啧啧啧.

于是我就入了数学（分析）这个大坑而无法自拔...

再更新(2019/8/6)：

事实上我所谓的“勾”大家应该都看出来了，是多项式函数的极值点，下面我们找出这种函数，以下全是爆算，推荐大家别看.

假设这个函数为

$f(x)=a_0+a_1x+a_2x^2+...+a_nx^n$

,也就是说

$f'(x)=a_1+2a_2x+3a_3x^2+...+na_nx^{n-1}$

的根为

$n-1$

个两两不相同的实根，也就是说

$f'(x)$

可以表示为

$f'(x)=\alpha\prod_{k=1}^{n-1}(x-b_k)，b_i\in\mathbb{R}$

，其中

$\forall i\neq j$

都有

$b_i\neq b_j$

.事实上显然

$\alpha=na_{n}$

.则积分得 :

$f(x)=\int_{0}^xf'(x)dx+f(0)=\int_{0}^x\alpha\prod_{k=1}^{n-1}(x-b_k)dx+a_0.$

事实上

$\prod_{k=1}^{n-1}(x-b_k)=x^{n-1}-\left(\sum_{1\leq k\leq n-1}b_k\right)x^{n-2}+\left(\sum_{1\leq i<j\leq n-1}b_ib_j\right)x^{n-3}+...$

$+(-1)^{k}\left(\sum_{1\leq i_1<i_2<...<i_k\leq n-1}b_{i_1}b_{i_2}...b_{i_k}\right)x^{n-k-1}+...+(-1)^{n-1}\prod_{k=1}^{n-1}b_k.$

$\int_{0}^x\prod_{k=1}^{n-1}(x-b_k)dx=\frac{x^{n}}{n}-\left(\sum_{1\leq k\leq n-1}b_k\right)\frac{x^{n-1}}{n-1}+\left(\sum_{1\leq i<j\leq n-1}b_ib_j\right)\frac{x^{n-2}}{n-2}+...$

$+(-1)^{k}\left(\sum_{1\leq i_1<i_2<...<i_k\leq n-1}b_{i_1}b_{i_2}...b_{i_k}\right)\frac{x^{n-k}}{n-k}+...+(-1)^{n-1}\left(\prod_{k=1}^{n-1}b_k\right)x$