想形成长期记忆,或者永久记忆,需要重复记忆多少天并且多少遍呀?
好久没有回答自己的专业问题了,让我们先定义一个概念:记忆半衰期[1](天)
记忆半衰期
顾名思义,就是你对某条记忆的回忆概率从 100% 下降到 50% 所需的时间(期间不进行任何重复)。
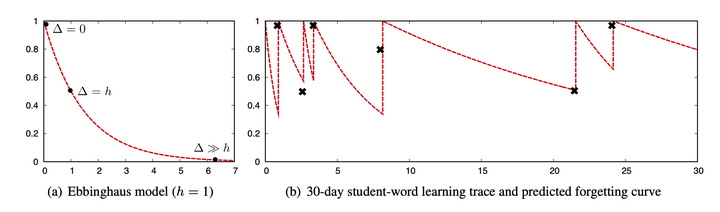
理论上,记忆半衰期不可能无穷大(至少目前人的寿命是有限的),所以永久记忆就不要想了。不过我们可以设置一个很长的记忆半衰期作为长期记忆的目标,比如十年,约 3650 天。
那么么题主的问题就变成了,需要重复多少次,才能使记忆半衰期达到 3650 天。
叶峻峣:KDD'22 | 墨墨背单词:基于时序模型与最优控制的记忆算法 [AI+ 教育]
我的 KDD 顶会论文正好就研究了相关问题:如何以最小的复习成本,让记忆达到目标半衰期。
若要回答这个问题,我们首先得研究记忆半衰期的变化规律:在重复记忆过程中,记忆半衰期是变长了还是变短了?变化了多少?受哪些因素影响?
记忆规律
在论文中,我提出了 DHP 记忆模型[2],其基于几条对墨墨记忆行为数据[3]的观察结果:
- 每次回忆成功时,半衰期将会增长,而回忆失败会导致半衰期下降
- 在半衰期较小时,半衰期增长的幅度更大
- 随着回忆概率下降,半衰期增长幅度上升
- 难度越大,半衰期增长幅度往往越小
比如下图,就显示了随着不断回忆成功,半衰期不断增长的情况:
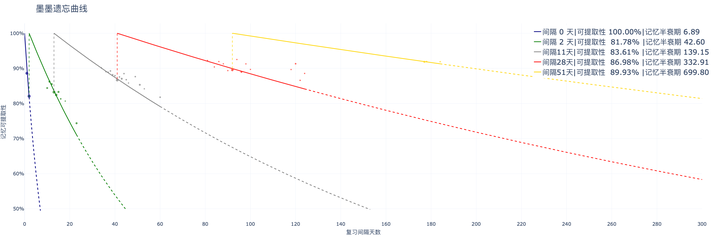
关于这些规律的更多观察,还请见我的论文,这里就不赘述了:
记忆模型
有了这些观察规律,我们就可以总结一个记忆模型来拟合、描述和预测记忆在重复过程中的变化了:
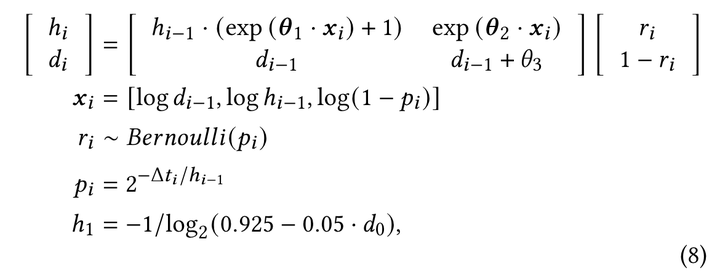
这就是 DHP 记忆模型的状态转移方程式。其中,h 表示记忆半衰期,d 表示记忆难度,p 表示回忆概率,r 表示回忆结果。
在墨墨开源记忆行为数据集上训练后,得到拟合参数并代入:
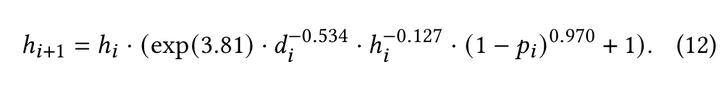
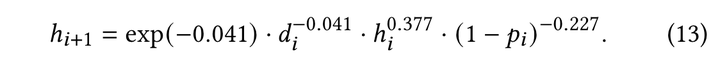
根据上面两个公式,给定初始条件,我们就可以预测任意记忆行为序列下的半衰期了。
最优策略
有了记忆模型,我们便可以开始着手寻找最优的重复策略。从现实出发,我们每一次重复都需要付出时间成本,而高效的重复策略即在最小的成本下形成尽可能稳定的长期记忆。我们可以把它转化为一个随机最短路径问题。
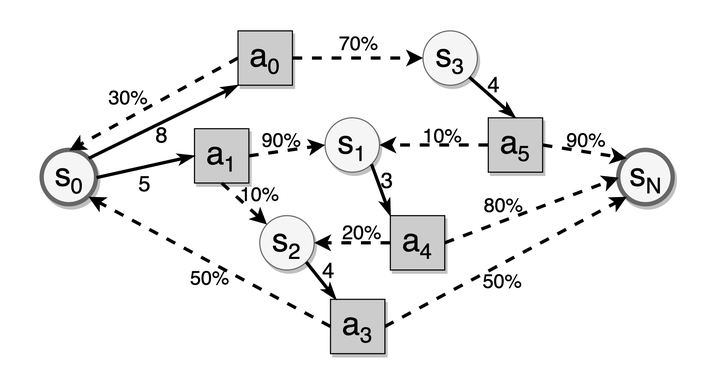
可能有些读者不知道什么是随机最短路径问题,我这里引用一段介绍:
The Stochastic Shortest Path problem (SSP) is a Markov Decision Process (MDP) that generalizes the classic deterministic shortest path problem. We want to control an agent, who evolves dynamically in a system composed of different states, so as to converge to a predefined target. The agent is controlled by taking actions in each time period1: actions are associated with costs and transitions in the system are governed by probability distributions that depend exclusively on the previous action taken and are thus independent of the past. We focus on finite state/action spaces: the goal is to choose an action for each state, i.e., a deterministic and stationary policy, so as to minimize the total expected cost incurred by the agent before reaching the (absorbing) target state, when starting from a given initial state.[4]
翻译:随机最短路径问题(SSP)是一个马尔科夫决策过程(MDP),是经典的确定性最短路径问题的更普遍的形式。我们想控制一个在由不同状态组成的系统中动态发展的智能体,以便收敛到一个预定的目标。智能体通过在每个时间段采取的行动进行控制:行动与成本相关,系统中的状态转移受概率分布的制约,这些概率分布完全取决于之前采取的行动,因此与过去无关。我们专注于有限状态 / 行动空间:目标是为每个状态选择一个行动,即一个确定的和固定的策略,以便在从给定的初始状态开始时,使智能体在达到(诱人的)目标状态之前产生的总预期成本最小。
把学习者代入智能体,记忆状态代入状态,复习代入行动,时间成本代入成本,回忆概率代入概率分布,把目前记忆半衰期代入目标状态,我们不难看出,寻找最优复习策略,就是在解决一个随机最短路径问题。
哦?题主想问的是重复记忆多少遍,和复习策略有什么关系?
很有关系。糟糕的复习策略可能会让学习者复习上千遍,也达不到目标状态。同时,我们是可以计算出不同复习策略的期望记忆次数的。这在我开发的 FSRS 算法中已经落地了:
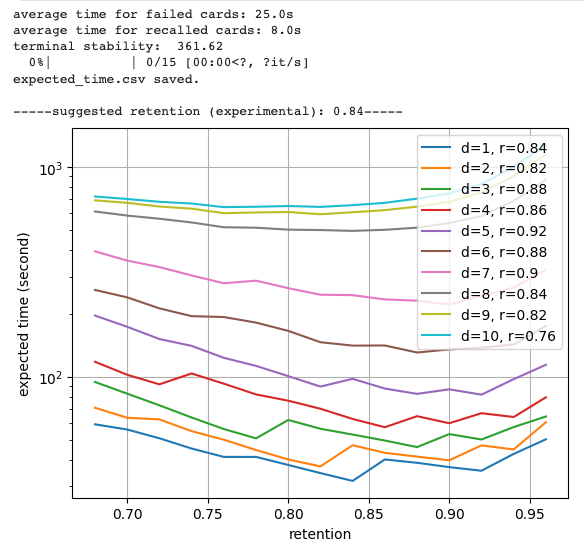
该图展示了在不同保留率(横坐标)复习时,不同难度的记忆材料(颜色)达到目标记忆稳定性(与记忆半衰期类似)的期望复习时间(纵坐标)。
可以看到,使用我自己在 Anki 上的 22 万次复习记录训练的记忆模型,给出的期望复习时间预测是,对于最简单的记忆材料,只需要十几秒的复习时间。对于最难的的复习材料,需要七百秒左右。
当然,这个预测只对我适用。不同的人、不同的记忆材料,会得到不同的结果。
回到我之前提的问题:需要重复多少次,才能使记忆半衰期达到 3650 天?
3650 天的记忆半衰期可以换算为 555 天的记忆稳定性(3650/log(0.5)*log(0.9)=554.8)
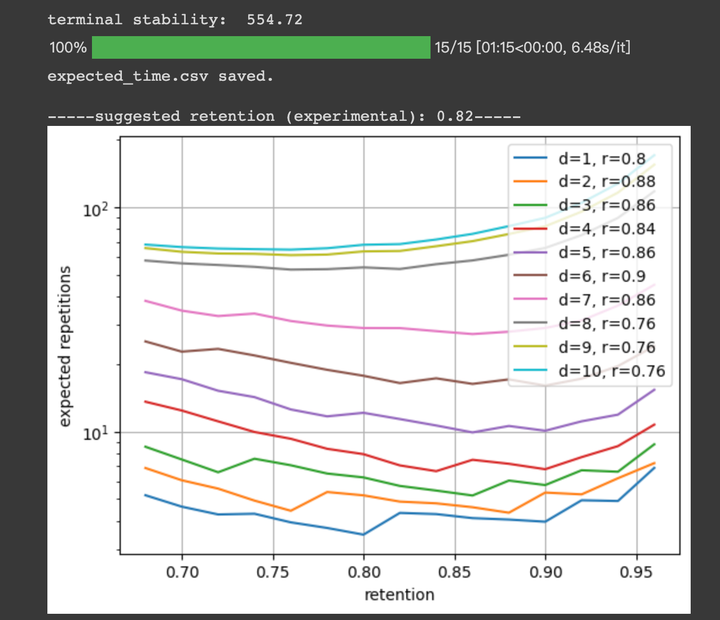
刚刚用我的数据跑了一下,最简单的记忆材料,只需要 4 次重复(期望值),最难的记忆材料,需要 70 次重复(期望值),普通的记忆材料,需要 10 次重复,记忆稳定性方可达到 554.72 天,约等于记忆半衰期 3649.4 天。
这个实验结果也应证了,卡片质量的重要性。垃圾卡片和优质卡片之间的记忆成本差了十几倍。切勿用战术上的勤奋(死记硬背)掩盖战略上的懒惰(知识理解)。
拓展阅读
欲了解更多有关记忆规律和复习算法的内容,请见:
叶峻峣:间隔重复记忆算法:e 天内,从入门到入土。叶峻峣:间隔重复记忆算法研究资源汇总叶峻峣:间隔重复记忆系统(Spaced repetition memory system)叶峻峣:0 目录《间隔重复的历史》
关于制卡相关的内容,请见:
叶峻峣:如何写出好卡片:利用间隔重复创造理解叶峻峣:Anki 高考的 20 条原则(1-5)—来自《有效的学习:组织知识的 20 条原则》
参考文献
[1] B. Settles and B. Meeder, “A Trainable Spaced Repetition Model for Language Learning,” in Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), Berlin, Germany: Association for Computational Linguistics, Aug. 2016, pp. 1848–1858. doi: 10.18653/v1/P16-1174.
[2] J. Ye, J. Su, and Y. Cao, “A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling,” in Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, in KDD ’22. New York, NY, USA: Association for Computing Machinery, 2022, pp. 4381–4390. doi: 10.1145/3534678.3539081.
[3] J. Ye, “Replication Data for: A Stochastic Shortest Path Algorithm for Optimizing Spaced Repetition Scheduling.” Harvard Dataverse, Mar. 08, 2023. doi: 10.7910/DVN/VAGUL0.
[4] M. Guillot and G. Stauffer, “The Stochastic Shortest Path Problem: A polyhedral combinatorics perspective,” European Journal of Operational Research, vol. 285, no. 1, pp. 148–158, Aug. 2020, doi: 10.1016/j.ejor.2018.10.052.

