要回答题主的问题,我们首先建立分划的概念,然后进一步解答问题答案。
1.首先建立分划的概念
我们在读实数理论时,会有一个很有趣的结论,就是任何一个无理数都是两个有理数序列的极限,其中之一从小于该无理数的方向向无理数无限逼近,另一个从大于该无理数的方向向无理数无限逼近。我们把小于该无理数的数列叫做不足数列,把大于该无理数的数列叫做过剩数列,见下图:
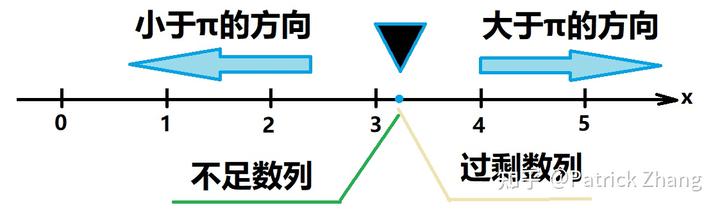
方便起见,我们不妨先以 3 这个有理数来分析:小于 3 的不足数列为(……,0,……,2.99,2.999,2.9999,2.99999,2.999999,……,3},注意上面左侧是圆括号,右侧 3 处是中括号,表示 3 包括在内。我们看到不足数列中的数小于或者等于 3。再看大于 3 的过剩数列为(……,3.0000001,3.0001,3.001,3.01,3.1,3.2,……,4,……),我们看到过剩数列中不存在最小数,亦不存在最大数。
在实数理论中,把不足数列和过剩数列叫做分划,用 A 表示。不足数列叫做下分划 A,过剩数列叫做上分划 A'。
2.有理数、无理数与分划的关系,实数理论中对有理数和无理数的解释
我们在翻看实数理论时,会看到如下几个概念:
对于有理数,A 中存在最大数,A'中则不存在最小数。或者反过来,A 中不存在最大数,而 A'中则存在最小数。一般地,我们都让 A 中取得最大数。故对于任意有理数,A 中有最大数,就是该有理数,而 A'中不存在最小数。
对于无理数,A 中不存最大数,A'亦不存在最小数。
定义 1:若某数列的全体值小于或者大于某个数,则称此数列为有界数列。若某数列的值均小于某数,则称此数列往上有界,且上界中的最小值就是数列的上确界;反之,若某数列的值均大于某数,则称此数列往下有界,且下界中的最大值就是数列的下确界。
对于有理数,A 中数列的极限就是该有理数,且 A 的上确界亦为该有理数。例如 3,A 中的数均小于或等于 3,3 就是 A 的上确界;而 A'中的数均大于 3,3 是 A 中数列的极限,同时也是 A'的下确界。
对于π或者无理数,无理数本身是 A 的上确界或者 A'的下确界。由于 A 或者 A'中的数列值都是有理数,故 A 中的数值永远无法取得π,A'中的数值亦永远也无法取得π。
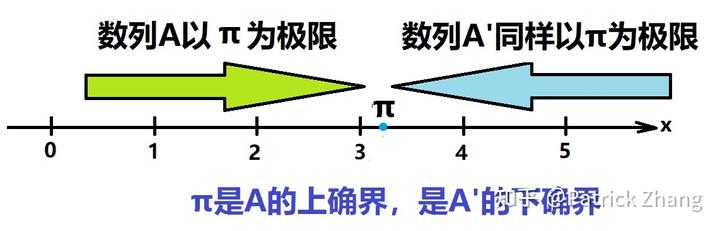
我们由此看出,对于某具体的无理数而言,该无理数就是分划 A/A'的极限。
3.关于稠密性
按照数系的规定,我们把全体整数、分数、有限小数都归于有理数系,把全体无理数都归于无理数系。
我们知道 3 和 4 都是有理数,我们要求它们中间的数,则把两者之和除以 2 即可:(3+4)/2=3.5,3.5 就是位于 3 和 4 中间的数。再例如 3 与 3.5 中间的数为 3.25,等等,我们可以把这种操作无限地做下去。
我们由此得知,任何两个有理数之间必然存在中间值。那么我们就会产生一个印象,就是有理数域是稠密的。然而真是如此吗?答案是:有理数并不是稠密的,3 与 4 之间至少被π给隔断了。任何两个有理数之间存在无穷多的无理数,它们都起到隔断作用。
由此可见,有理数域和无理数域都不是稠密的,只有它们的合体也即实数域才是稠密的。
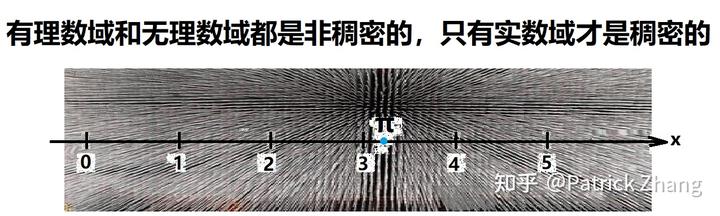
还有一个很有意思的现象:我们列写整数序列:1,2,3,……,1000000,1000001,……。我们还可以列写 0 和 1 中间的分数序列:1/1,1/2,1/3,……,1/1000000,1/1000001,……。我们发现这两个序列是对等的,整数序列可以写多长,分数序列也可以写多长。可见,整数序列的整数数量与 0 到 1 间分数序列的数量一样多!是不是有点奇怪?这说明什么?
4.关于上述定义和结论的来源
以上的所有定义和结论,请参阅任意一本数学分析的实数理论部分。我的参考书就是我读过的课本——复旦大学的《数学分析》中的实数理论部分。
5.题主的问题答案
通过以上表述,我们很容易知道,用计算机计算π无非就是在 A 中计算或者在 A'中计算,而且给出的数值都是有理数。虽然已经计算了 30 多万位,但不可能穷尽的。

哪怕我们列写出图 4 百度图片中π的小数点后 1000000 位(局部),但这个数依然是有理数,而且属于 A 的序列范围,不是真正的π。可见,我们只能无限地向π逼近,永远也不可能写出真正的π。
那么计算机计算π有何意义?主要就是考核某台计算机的计算速度和计算精度,与π是否会被穷尽毫无关系。
这就是题主问题的答案。
图 5 是计算π的公式之一:
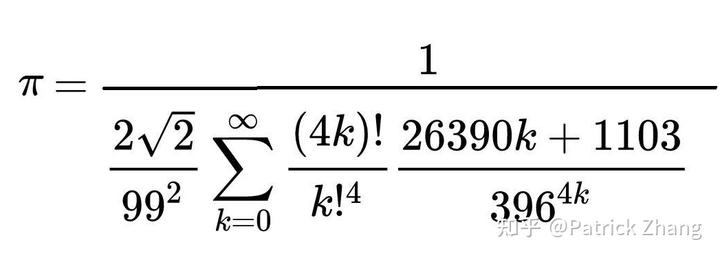
类似的公式很多,有一本书《揭开π的奥秘》是日本数学家写的科普书,里面给出了大量的计算公式。
N 久以前我和几位同事还真的在 PC 机上编了 BASIC 语言程序去算π,算了 5 分钟左右,打印出来有多少页及位数都忘了,当时感觉非常惊讶。由于纸张浪费太多,还被办公室负责人责怪。

当时的 PC 机很慢,现在的电脑和笔记本当然快多了,在相同的时间里肯定能计算出更多位,产生更多的废纸,笑!
可见,题主的主题假设是不存在的。
某日我家一位亲戚小女孩来玩,她今年 9 月要读初三了。谈起初中数学的学习,我问她:什么叫做有理数和无理数?它们之间有何关系?小女孩说前者是有限小数或者整数及 0,后者是无限不循环小数。至于关系嘛就说不出来了。
我用分划理论给她讲解了有理数、无理数和实数,她听得津津有味,之后她说彻底弄明白有理数与无理数的关系了。我把《数学分析》中有关实数理论部分复印给她,还送她一本《第一次到第三次数学危机》的书给她,让她暑假仔细阅读。
我们家这位亲戚小女孩很喜欢数学,但却提不出类似题主的问题。可见,题主还是很厉害的,想法不错。
就写到这里。
我到当当网看了,我的课本——复旦大学的《数学分析》早已绝版。建议题主到图书馆中去看任何一本《数学分析》,找到其中的实数理论部分,应当能看到上述定义和结论吧。

