谢邀。
六方最密堆积和面心立方最密堆积都是:“最密堆积”,它们的空间占有率都是 74%,处于所有等价刚球密堆积(注意这些名词!)当中空间利用率最高的。
这个数字你可以用硬球模型推导出来,主要把握两个量:
(1)单位原包中所含有的硬球个数(这里假设每个球大小都一样。你也可以想想如果不一样的话空间利用率会提高到多少?)
(2)通过球之间的相互作用方式计算出原包的各个边的长度(因此可以求体积)
然后把这两个量相除就能得到空间占有率了。(具体推导可以参见:[转载]六方最密堆积的计算_biqin_新浪博客)
除了最密堆积之外,还有其他的堆积方式:
- 体心立方堆积:68%
- 简单立方堆积:52%
- 钻石结构:34%
- 随机堆积:59%~64%
那么下面来说说六方最密堆积和面心立方堆积的区别。
首先我们先看看最密堆积的一个表面:
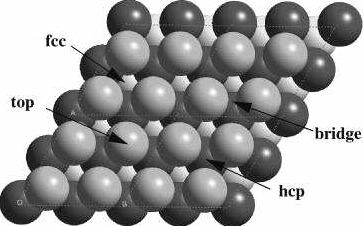
(图 1. 来自 Google)
我们可以很清楚的看到,对于 3-fold 位点(也就是这个位点由三个原子构成的),有 hcp、fcc 两种。因此要想弄清楚六方最密堆积和体心立方最密堆积的区别,就要了解它们是通过什么方式得到的。
六方最密堆积:
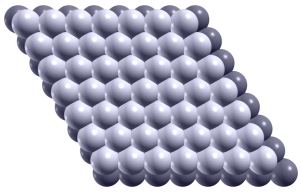
如果我有一层密堆积的表面:

(图 2)
我们再这层下面加上第二层原子。由于第一层当中所有三配位的位点都是一样的,因此第二层放在哪里不会有任何问题。但是由于第二层和第一层错开了,因此我们假设第一层为 A,第二层为 B。
(图 3. 浅灰色代表 A 层,而深灰色代表 B 层)
接下来的第三层的摆放决定了这个结构是六方最密堆积还是面心立方最密堆积:
- 如果第三层放到和第一层一样的地方:这时我们得到了ABAB.....的结构,这就是六方最密堆积。
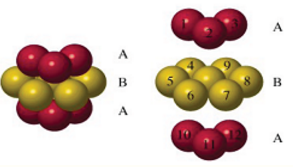
(图 4. 注意上下两个红色的方向)
- 如果第三层放到和第二层、第一层都不一样的地方(参看图 1,第一层为原子位,第二层假设放到 hcp 位点,则第三层放到 fcc 位点)。这时我们得到了ABCABC.....的结构,这就是面心立方最密堆积。
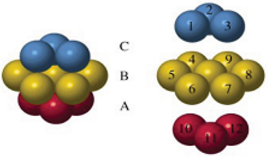
(图 5. 上面蓝色和下面红色的方向相反)

