量子鸽巢效应
一般我们知道,如果把三个鸽子放在两个洞里,那么至少有两个是会在同一个洞里的,这个成为鸽巢原理,又叫抽屉原理。数学一点的表述是,如果要把 n 个对象分配到 m 个容器中,必有至少一个容器容纳至少[n/m]个对象。

量子鸽巢效应是什么呢,即使你有 n 个“鸽子”,n-1 个“巢穴”,你也找不到两个在同一巢穴的鸽子,神不神奇?惊不惊喜?
下面这张图讲的很明白了,用后选择(post-selection)或者弱测量(weak measurement)的方法可以实现这个效应:
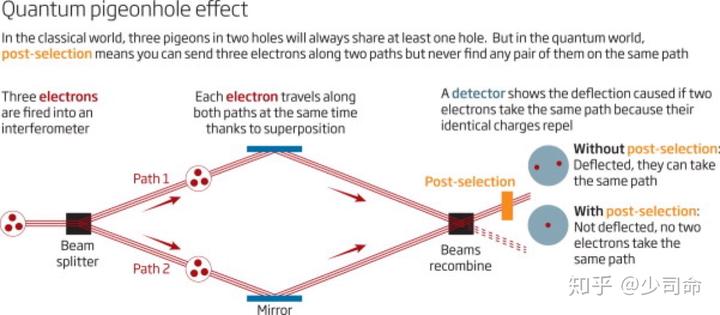
虽然并没有什么关系, 不过以后放鸽子时候又多了一个理由

所以我有时间再来补充详细的细节,这回不鸽了(逃)
两天前写的答案窝来填坑了....
有些人这个具体原理是什么,我尽量用简单的语言来回答,学过量子同学可以直接参考[1]那里面讲的挺清楚的。
考虑下面的一个干涉仪(大家高中物理都学过了吧)
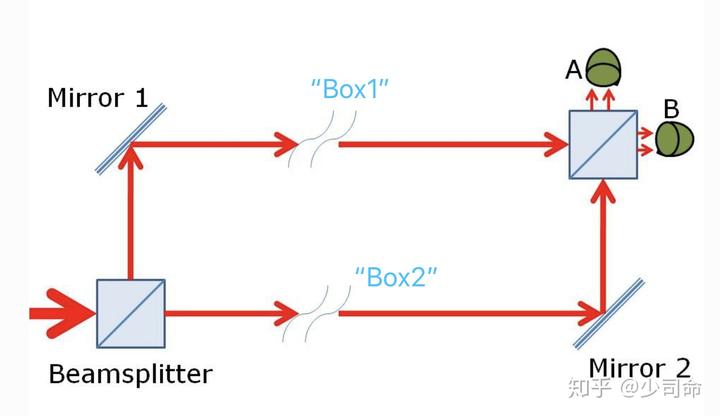
假设我们有三个光子(相当于三个“鸽子”)从左边进来,经过两个 arm(相当于两个"鸽巢"),最后再经过一个 BS 后被两个探测器 A 和 B 接收,不考虑光子的损耗,每个光子有可能进入 A 也有可能进入 B,所以我们得到 8 种可能性:AAA, AAB, ABA, BAA, ABB, BAB, BBA, BBB.
然后我们做一个后选择(post-selection),即考虑最后探测器测到 AAA 或者 BBB 时,中间光子在经过两个 arm 时候到底发生了什么。从 AAA 或者 BBB 的这个结果我们可以推出光子在 arms 时的波函数
. 另外我们定义有两个光子在同一个 arm 的对应的波函数为 {
}. 数学书可以证明这两个是正交的。也就是说,当我们测到 AAA 或者 BBB 时候,光子在 arm 中时候“没有两个光子是在同一个 arm 的”. 这个数学推导其实非常简单,在[2]里面有详细过程。
这里的关键是,这两个波函数正交,也就是说当你对任意两个光子做一个 joint measurement (不知道中文应该怎么翻译, 共同测量?) 时候,你可以知道他们并不在同一个 arm 里,而并不知道到底哪个在哪个。这种 joint measurement 和量子通讯里常用的量子远程传态里面的做法是一样的。
大家开始的理解可能是,我先测一下光子 1,找到所在的 arm,然后我再测一下 2, 然后看他们是不是在同一个 arm 就好了。但其实这里的情况并不是这样的,你需要测的是它们在不在同一个 arm,而不是哪个具体在哪个 arm. 这个效应我觉得还是蛮有趣的,至少会对人们对 quanutm correlation 的理解有所帮助。
量子鸽巢效应最早是在 2016 年初的时候在一篇 PNAS[2]文章里提出来的(当然 arXiv 更早是在 14 年),实验验证的难点应该是怎么设计实验既可以做后选择又可以测出中间态。
刚刚搜了一下发现几天前四月底时候就有一篇相关的实验文章[3],用 IBM 的 SC circuits 做的,还没仔细看.....等周末再更实验部分,争取不鸽

