之前写过两篇关于傅立叶变换的文章：

• 如何直观地理解傅立叶变换？
• 如何理解傅立叶级数公式？ （后面此文简称“代数细节”）

傅立叶级数是针对周期函数的，为了可以处理非周期函数，需要傅立叶变换。如果对傅立叶级数有疑问，请参看“代数细节”一文。

先看下思路：

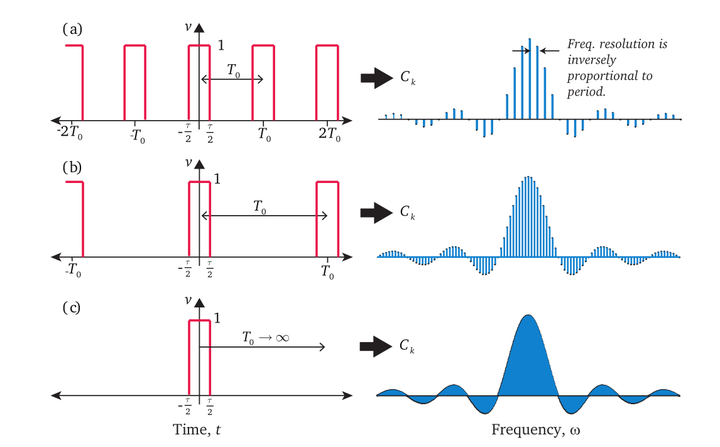
• (a).周期函数，可以通过傅立叶级数画出频域图
• (b).增长周期，频域图变得越来越密集
• (c). ，得到傅立叶变换，频域图变为连续的曲线

下面是细节的讲解。

1 傅立叶级数

让·巴普蒂斯·约瑟夫·傅里叶男爵（1768 －1830）猜测任意周期函数都可以写成三角函数之和。比如下面这个周期为

的方波，可以用大量的正弦波的叠加来逼近：

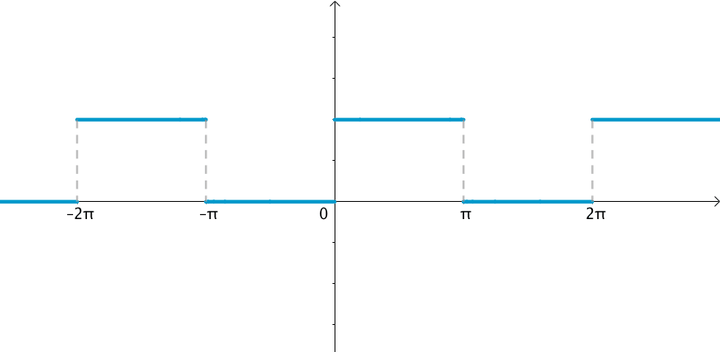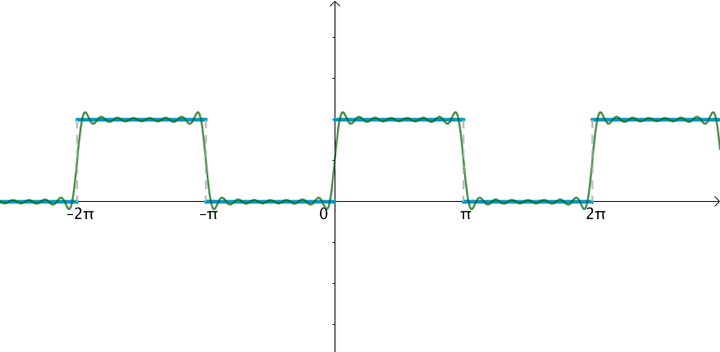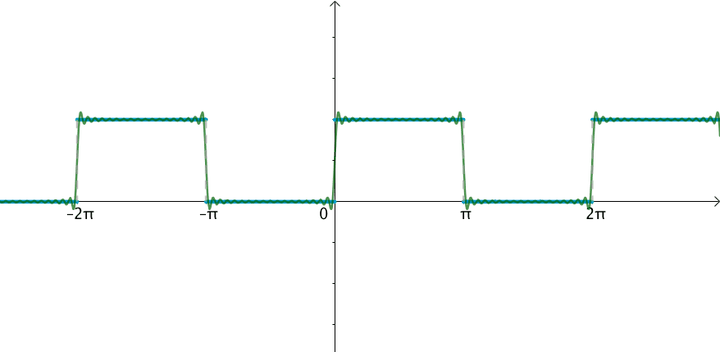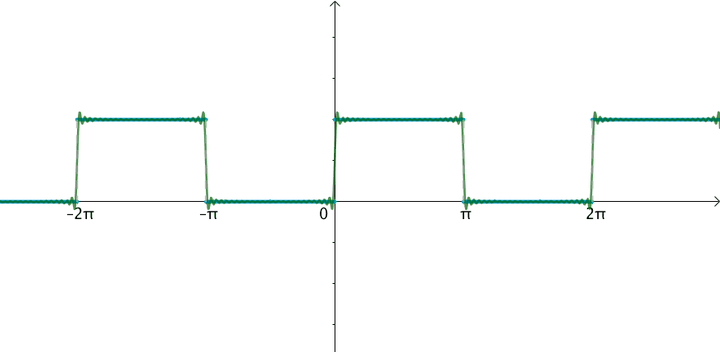
1.1 傅立叶级数是向量

从代数上看，傅立叶级数就是通过三角函数和常数项来叠加逼近周期为

的函数

：

在“代数细节”一文中解释了，实际上是把

当作了如下基的向量：

那么上面的式子就可以解读为：

说具体点，比如刚才提到的，

的方波

，可以初略的写作：

从几何上看，有那么一丁点相似：

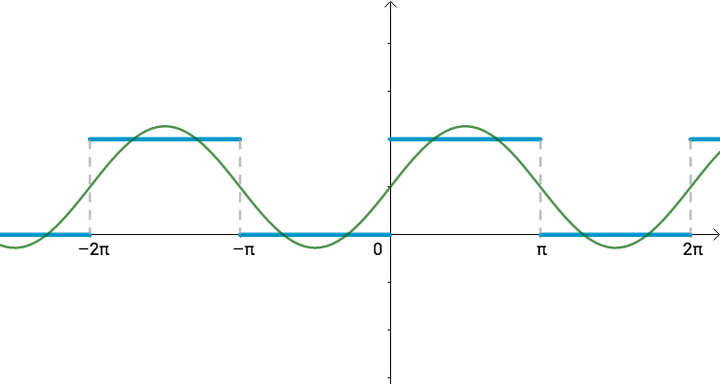
我们可以认为：

此函数的基为：

则

相当于向量：

画到图上如下，注意坐标轴不是

，而是

：

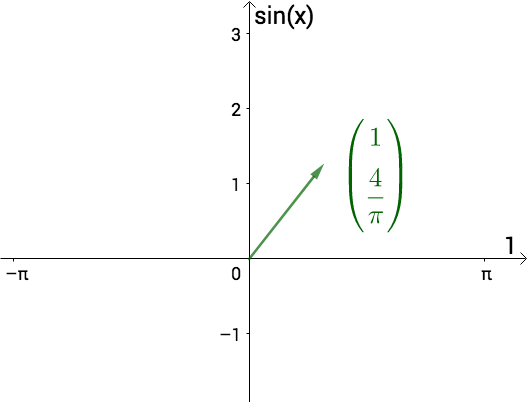
1.2 频域图

再增加几个三角函数：

从几何上看，肯定更接近了：

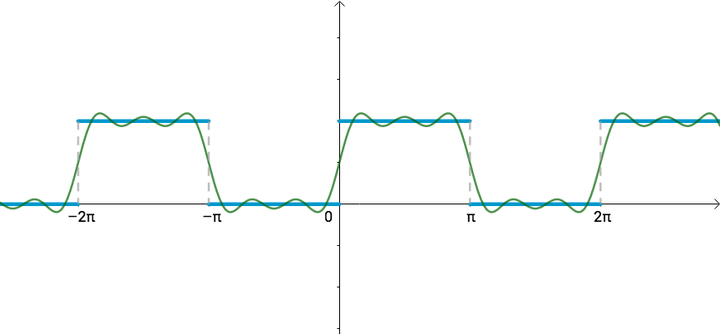
此时基为：

对应的向量为：

六维的向量没有办法画图啊，没关系，数学家发明了一个频域图来表示这个向量：

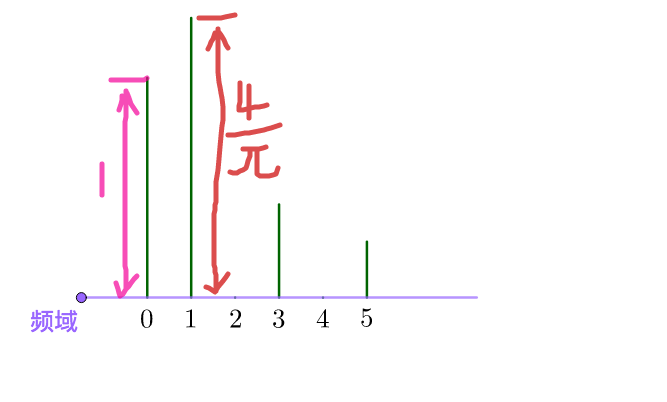
上图中的

分别代表了不同频率的正弦波函数，也就是之前的基：

而高度则代表在这个频率上的振幅，也就是这个基上的坐标分量。

这里举的例子只有正弦函数，余弦函数其实也需要这样一个频谱图，也就是需要两个频谱图。当然还有别的办法，综合正弦和余弦，这个后面再说。

原来的曲线图就称为时域图（这点请参考“代数细节”），往往把时域图和频域图画在一起，这样能较为完整的反映傅立叶级数：

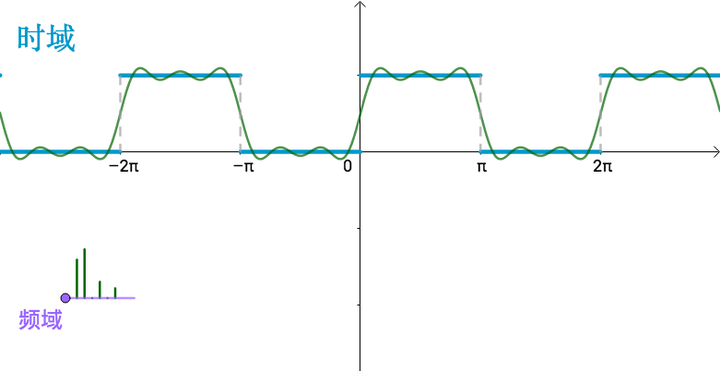
不管时域、频域其实反映的都是同一个曲线，只是一个是用函数的观点，一个是用向量的观点。

当习惯了频域之后，会发现看到频域图，似乎就看到了傅立叶级数的展开：

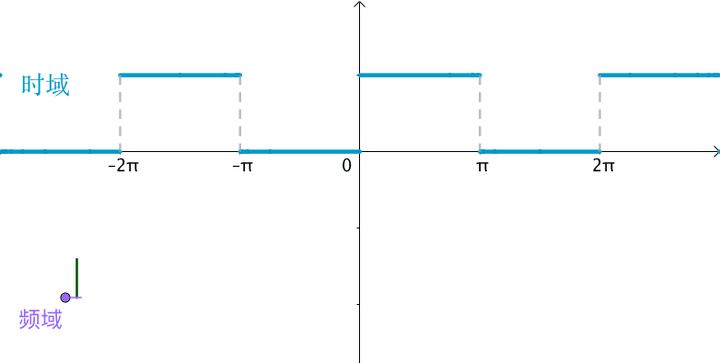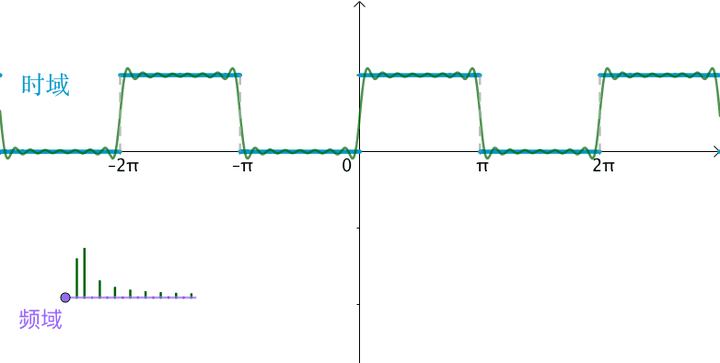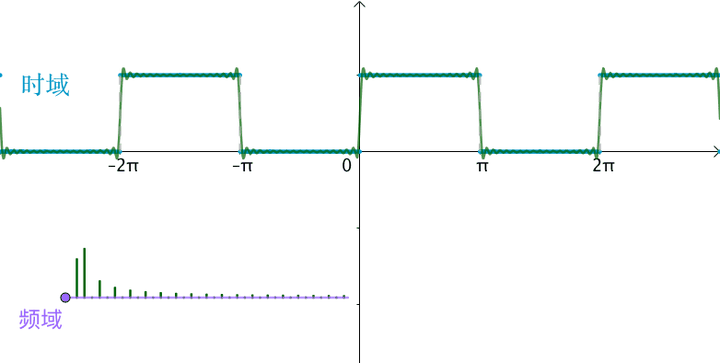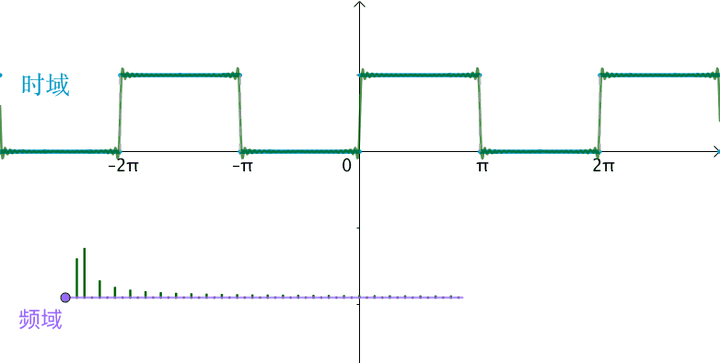
2 非周期函数

非周期函数，比如下面这个函数可以写出傅立叶级数吗？

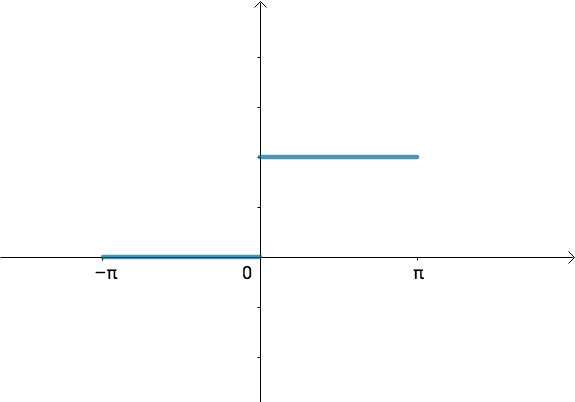
这并非一个周期函数，没有办法写出傅立叶级数。

不过可以变换一下思维，如果刚才的方波的周期：

那么就得到了这个函数：

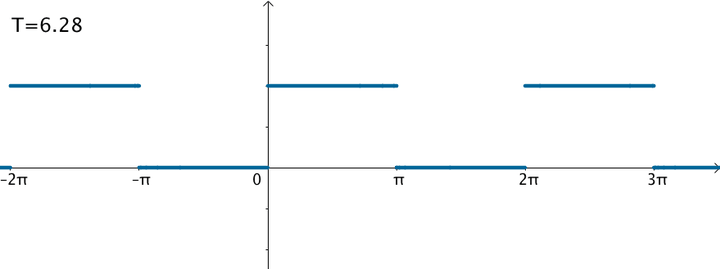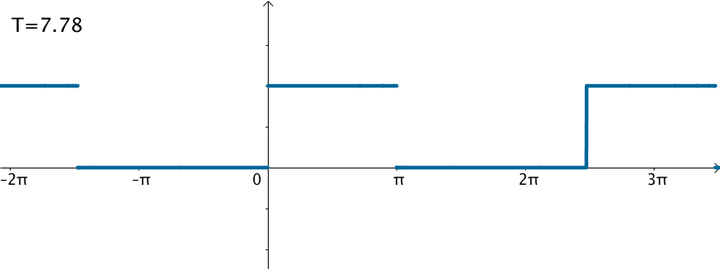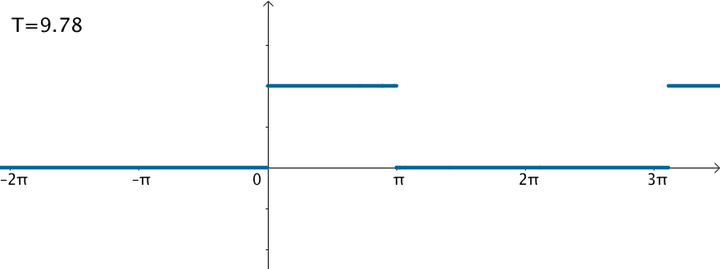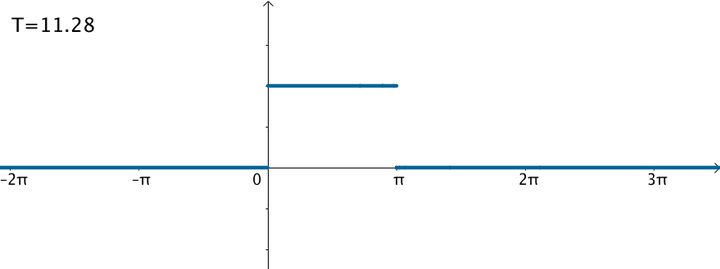
在这样的思路下，就可以使用三角级数来逼近这个函数：

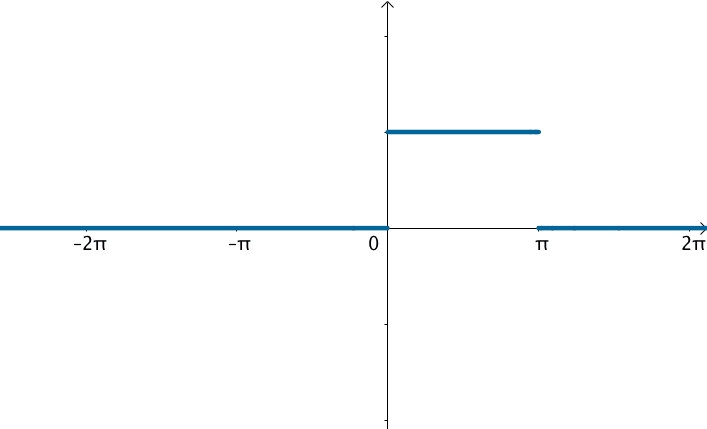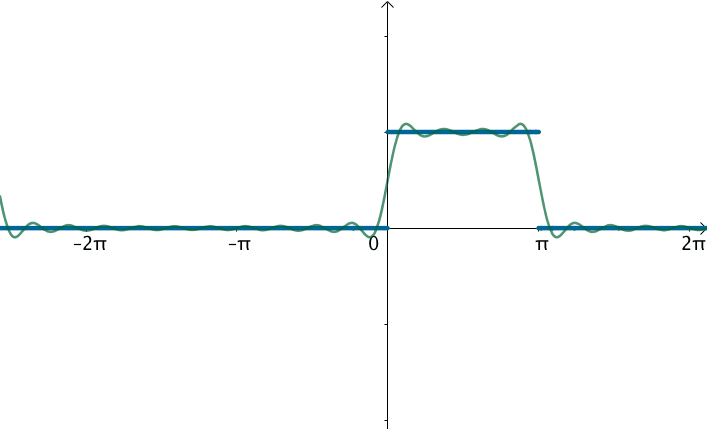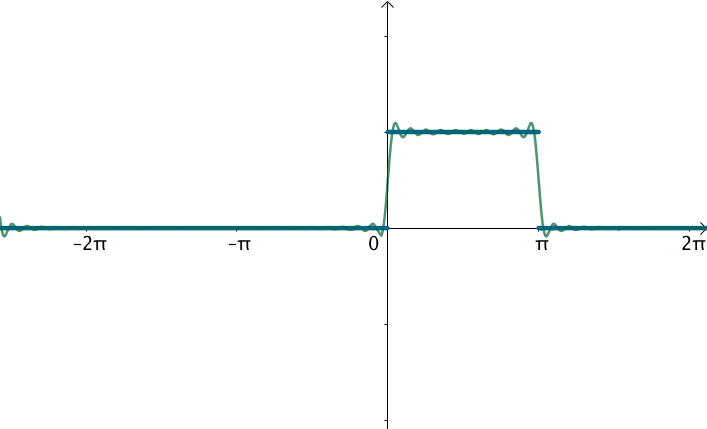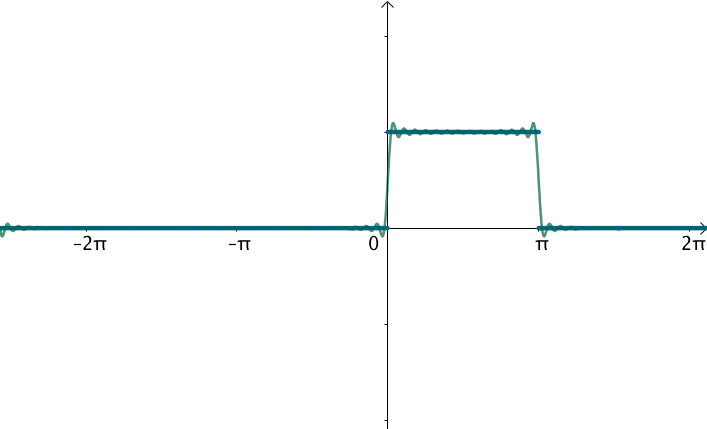
观察下频域，之前说了，对于周期为

的函数

，其基为（对此点有疑问的，可以看“代数细节”一文）：

刚才举的方波

，对应的基就为（没有余弦波）：

对应的频率就是：

按照刚才的思路，如果

不断变大，比如让

，对应的基就为（没有余弦波）：

对应的频率就是：

和刚才相比，频率更加密集：

之前的方波的频域图，画了前 50 个频率，可以看到，随着

不断变大，这 50 个频率越来越集中：

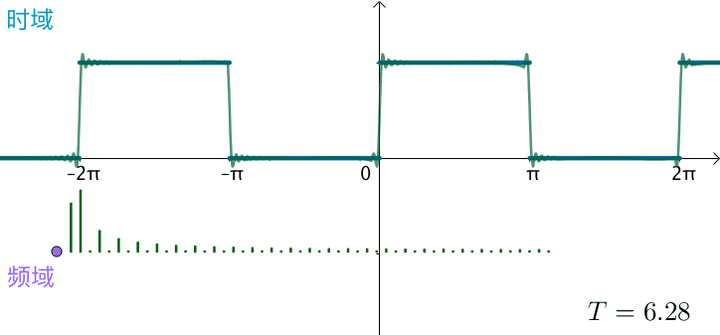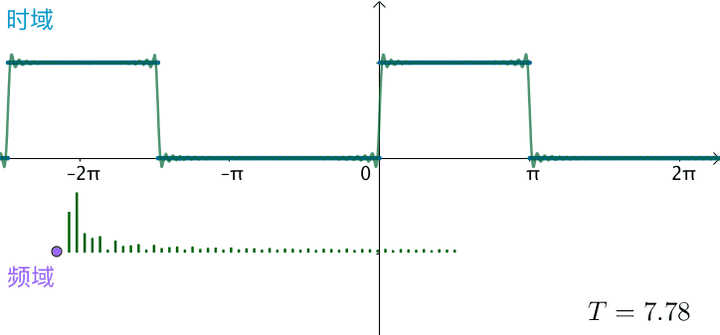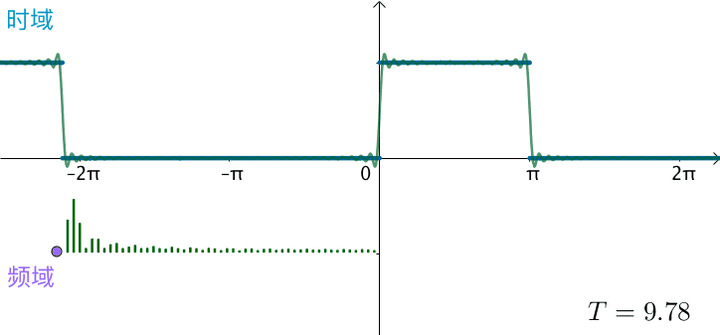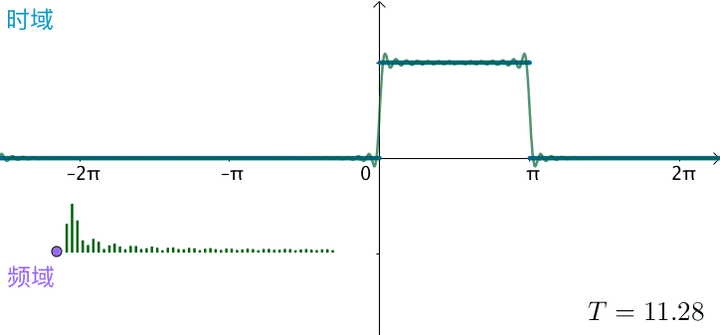
可以想象，如果真的：

这些频率就会变得稠密，直至连续，变为一条频域曲线：

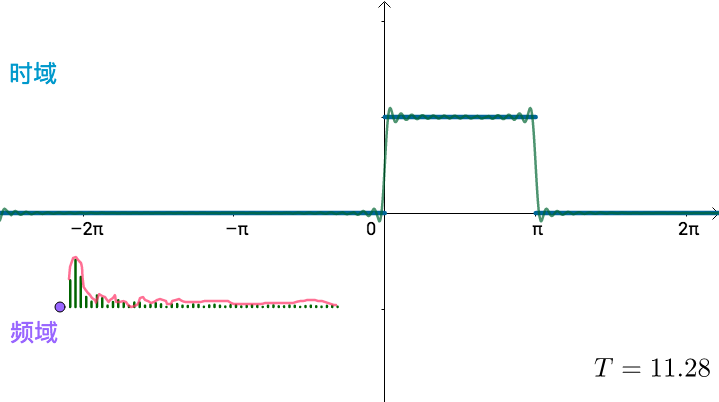
傅立叶变换就是，让

，求出上面这根频域曲线。

3 傅立叶变换

之前说了，傅立叶级数是：

这里有正弦波，也有余弦波，画频域图也不方便，通过欧拉公式，可以修改为复数形式（请参考“代数细节”一文）：

其中：

复数形式也是向量，可以如下解读：

不过

是复数，不好画频域图，所以之前讲解全部采取的是三角级数。

周期推向无穷的时候可以得到：

上面简化了一下，用

代表频率。

大致是这么得到的：

就是傅立叶变换，得到的就是频域曲线。

下面两者称为傅立叶变换对，可以相互转换：

正如之前说的，这是看待同一个数学对象的两种形式，一个是函数，一个是向量。

更多内容推荐马同学图解数学系列教程

文章最新版本在（有可能会有后续更新）：从傅立叶级数到傅立叶变换