关于为什么三维空间内共有 230 种空间群,要先从点群开始说起。而在此之前,我们要先知道什么是群(group),或者说得更清楚一点,什么是晶体学群(crystallographic group)。
对于一个给定的实物晶体,将其中的对称操作进行编号
(
),在编号后,讲两操作倒序书写并在中间增置一个低位点
,表明其顺序连续操作。如
意味先执行位于后方的
操作,再执行
操作。
当
时,
一般都用于指代恒等变换
。
以石英晶体为例,其蕴含的对称操作及其编号如下

群(group)
我们可以从直观上说,群是满足某些条件的关于对称操作的集合(set)。
为了使对称操作的集合
成为给定操作[1]下的合法群,有下述共计 4 个基本要求须被满足使之成其所是。
- 操作空间的封闭性(operation space is closed)
属于集合
的任意两操作之低位点积仍属于该集合。
- 积法操作符合乘法结合律(multiplicative operation is associative)
- 包含恒等算符(unit/neutral/identity operator)
- 每个元素都有其逆元素
满足上述四个基本要求的、在一定积法规则下的集合
称为一个群。
阿贝尔(Abelian)群
若在一个群中,积法操作的顺序不实际影响其结果,即
称该群为一个交换群(commutative group)或阿贝尔群(Abelian group)。
晶体学群(cryrtalllographic group)
任何实际存在的晶体内部的对称操作的集合都可构成群,晶体学群(crystallographic group)拥有确定的名字(definite designation),如对于上文出现过的石英,其 Hermann-Mauguin symbol 为
。
若群中所有积法操作都被声明,称该群被完备确定(determined)。为表明所有积法关系,可使用 Cayley 表。石英(
)的 Cayley 表为

Abelian 群的 Cayley 表沿主对角线对称。
点群(point group)
任意点群均可经由 Seitz symbon 被表示为
由此可见,点群所表述的对称要素[2]均相交于同一点,即原点(origin);即当该 Seitz symbon 与原点坐标
相乘后,其所得到的变换后坐标永远仍为坐标原点
,这也是点群被称为点群的原因。
三维晶体学点群共有 32 个[3],容纳对称操作的合并和对称操作的连续执行,但不引入平移对称操作,否则将导致 230 个空间群。
点群有固定的图像表述方式,被称为球极平面投影(sterographic projection),在图像中表述中,位于左上角、右上角、和左下角的符号分别表示该点群的 Hermann-Mauguin notation,Schönflies notation,和点群阶(point group order)。
以最简单的
点群(即仅包含恒等算符)为例,其直观图和球极平面投影如下,
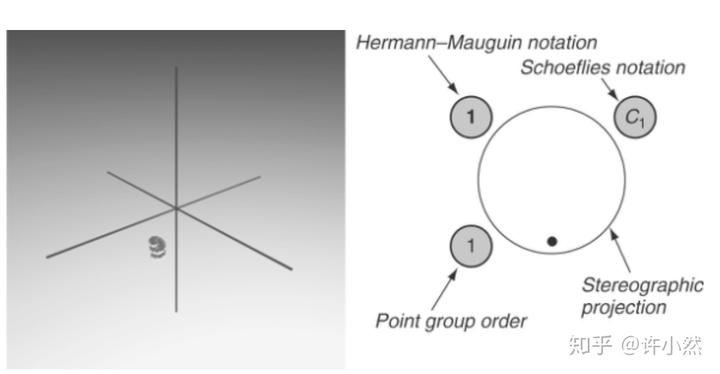
点群阶是点群内诸对称操作所产生的 motif 数目,若该数目有限,称该群为一个有限群(finite group)。
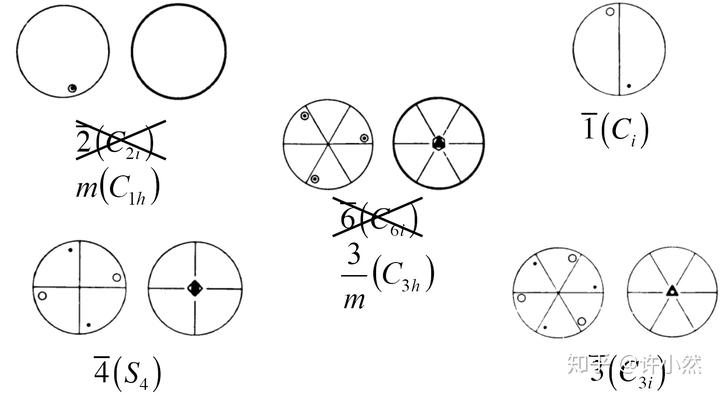
你可能听说过这样一个结论:在三维空间共有 32 种不同的点群,那么它们是怎么来的?
32 点群的导出第一步:真旋转群(cyclic/proper rotation group)
基本操作群,共计 5 个。
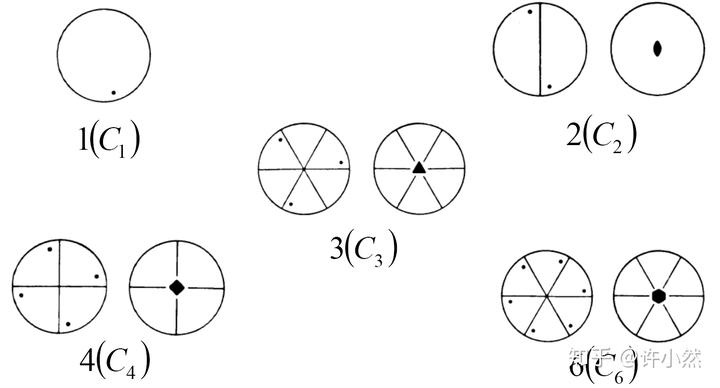
第二步:水平对映旋转群(cyclic+horizontal mirror group)
水平对映操作即对映面平行于作图平面,水平对映在 Hermann-Mauguin notation 上被表示为
。水平对应旋转群共计 5 个,目前已导出 10 个三维点群。
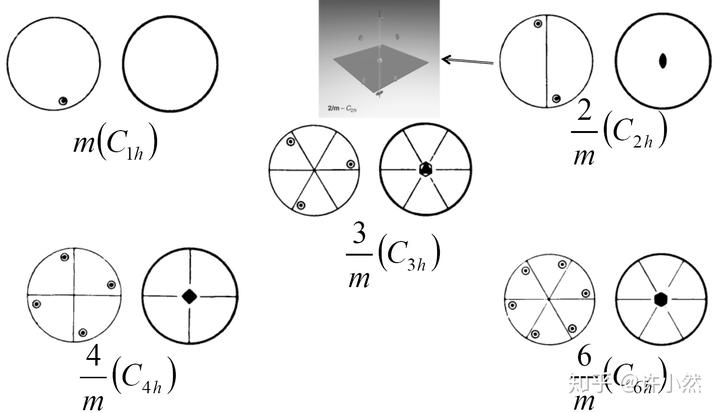
第三步:垂直对映旋转群(cyclic+vertical mirror group)
垂直对映即对映面垂直于作图平面,由于
重垂直对映旋转群和
重水平对应旋转群在绝对空间关系上等效,因而垂直对映旋转群共有 4 个,目前已导出 14 个三维点群。
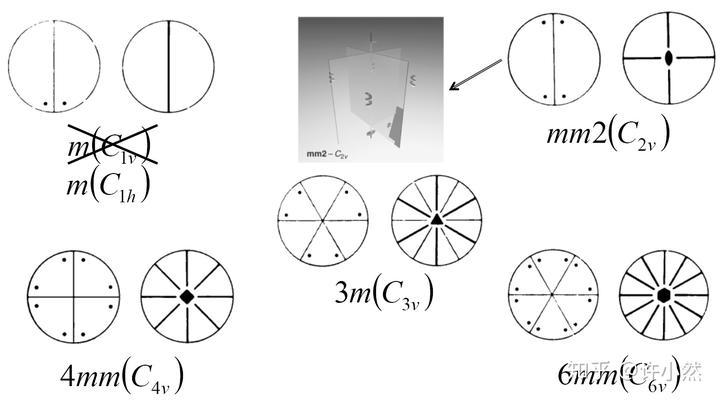
第四步:旋转反演群(rotation+inversion)
由于
重旋转反演群与
重旋转垂直 / 水平对映群在绝对空间关系上等效,
重旋转反演群与
重旋转水平对映群在绝对空间关系上等效,旋转反演群共有 3 个,目前已导出 17 个三维点群。
第五步:旋转之旋转群 & 旋转之旋转之旋转群(combination[4] of pure rotations)
合法的旋转 combination 群可由 Euler 定理得到。绝大多数对称要素的 combination 都是非法的。若随机选取两个旋转轴并将其以随机角度放置,这很有可能会导致非法组合。旋转对称性需要考虑到晶体学的实际范畴。
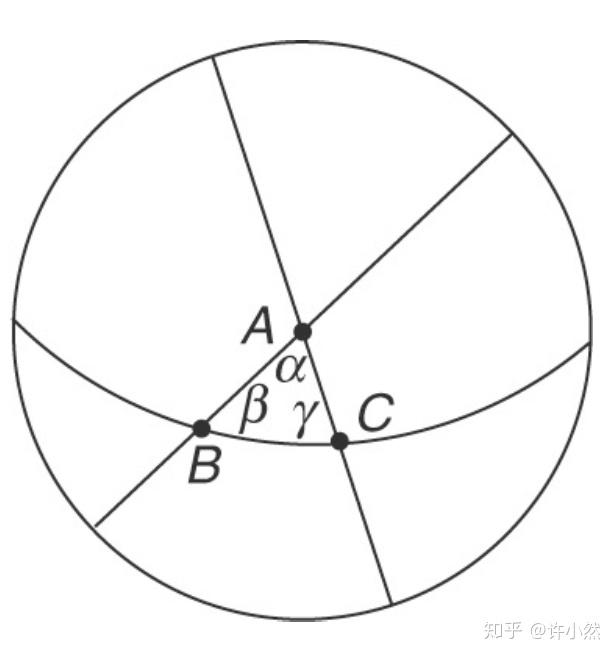
以两个
重旋转轴以
放置的 combination 为例,其暗示了
重对称性,这在结晶学中不存在,因而该 combination 非法。
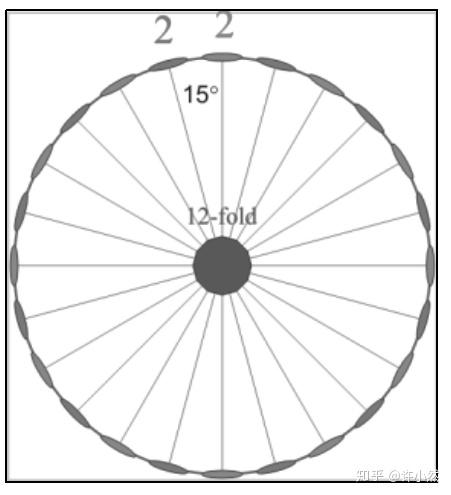
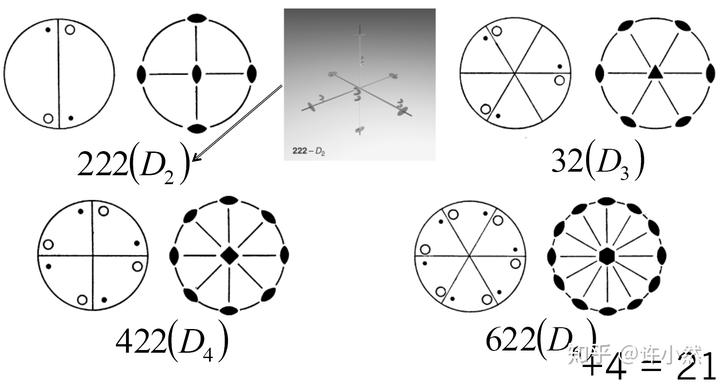
二面体群(dehedral group)
二面体群指对垂直方向的
重对称操作进行合法旋转对称操作构成的群。
二面体群共有 4 个,目前已导出 21 个三维点群。
二面体对映群(dihedral group+mirror plane)
垂直于和位于旋转轴的对映面都被展示,旋转轴和每种对映面的其中一面需要作为群生成元(group generator)出现,旋转轴寓居于对映面中。
二面体对映群共有 4 个,目前已导出 25 个三维点群。

二面体对映反演群(dehedral group+mirror plane+inverse rotation)
二面体对映反演群是旋转反演对称操作和旋转轴在其上的对映面的 combination。
二面体对映反演群共有 2 个,目前已导出 27 个三维点群。
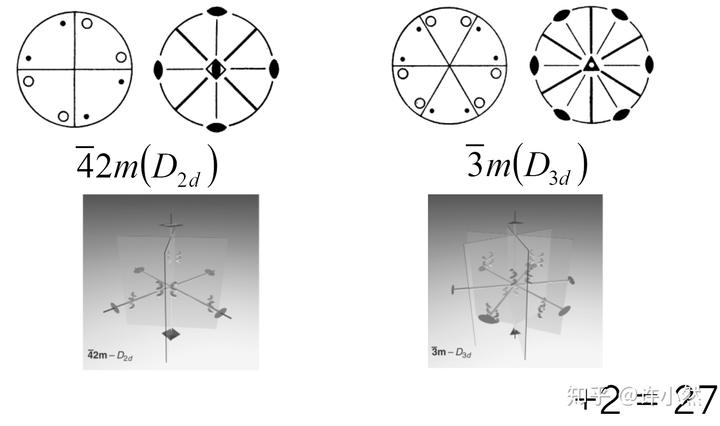
四面体群(T group,tetrahedral group)
在四面体群中,
重旋转轴按照立方晶系的诸主方向放置(the two-fold axis is oriented along the primary direction of the cubic crystal system),而
重对称轴则沿次方向(secondary direction)放置。
四面体群共有 3 个,目前已导出 30 中三维点群。

八面体群(O group,octahedral group)
在八面体群中,
重对称轴沿主方向放置,
重对称轴沿次方向放置。
八面体群共有 2 个,全部 32 三维点群已被推导完成。
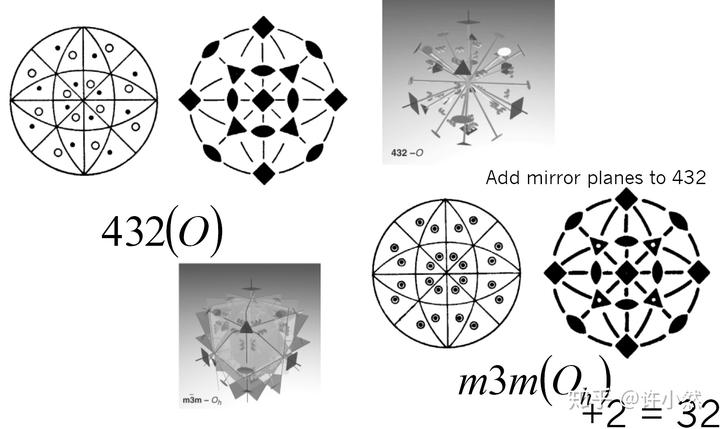
点群的矩阵表示
由于点群不涉及平移对称性,因而采用三阶方阵表示其蕴含的每一个对称操作,并用 Cayley 表对点群进行完备确定。
依然以最初的石英的
点群作为例子,其矩阵和 Cayley 表述如下,
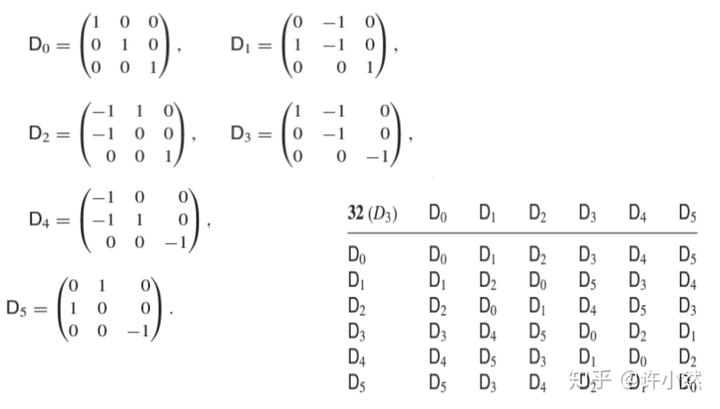
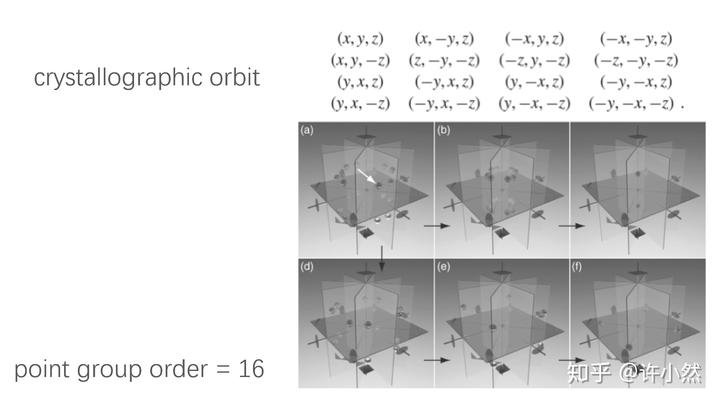
一般点(general point),结晶学轨道(crystallographic orbit),点群阶
对于一给定点群,其中某一般点
经历该点群内所蕴含的全部对称操作所得到的所有对称等效(symmetrically equivalent)的集合称为结晶学轨道。
结晶学轨道内对称等效的一般点的数目即为点群阶。
以二面体对映群
为例
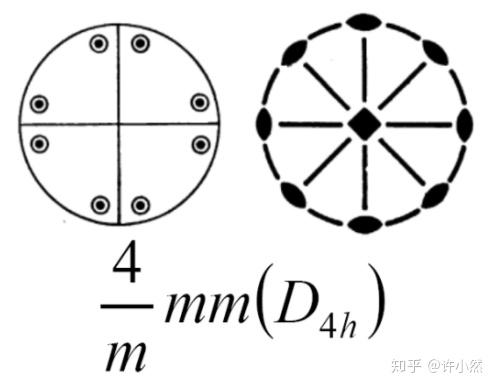
其结晶学轨道、直观图、和点群阶为
特殊点(special point)& 席对称性(site symmetry)
The site-symmetry group (also called point symmetry) of a point is the finite group formed by the set of all symmetry operations of the space group of the crystal that leave that point invariant. It is isomorphic to a (proper or improper) subgroup of the point group to which the space group under consideration belongs. In general, the origin is a point of highest site symmetry.
我们取 site symmetry 的日文翻译:席对称性;而不是其中文翻译:位对称性群或点对称性,因为前者具有术语的特殊性,不容易在语句中混淆。严格翻译应该认为席对称性的全称为席对称性群,是其所在点群的子群,但我们姑且不做这样细致的辨析。
总之,席对称性指的是在点群中某一确定点的局域对称性。
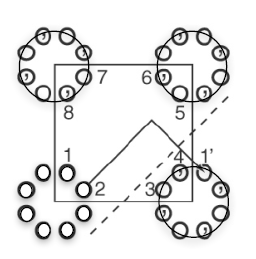
依然以二面体对映群
为例,若将一般点
移动至
轴得到一特殊点
,则其结晶学轨道中的 16 个一般点均会合并到
轴上的两个点。这意味着对于特殊点
来说其结晶学轨道只包含两个点
和
。该特殊点
位于
重对称轴和蕴含
重对称轴的对映面[5]上,故该特殊点的席对称性为
。
完全一般点的席对称性为恒等算符,而特殊点拥有更高的席对称性。
Wyckoff 位置
依然以二面体对映群
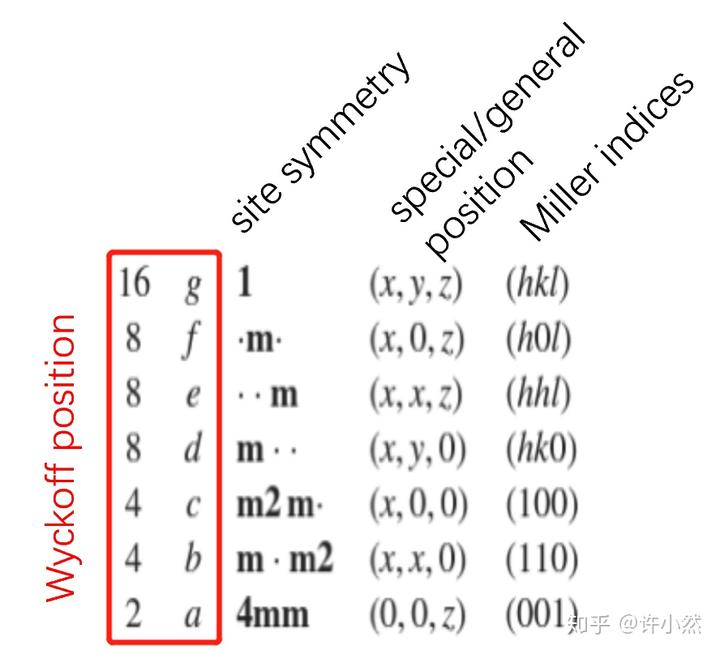
为例,总结其内诸一般点和特殊点,
- 将对应的结晶学轨道内对称等效的位点数目放在第一列,从上到下数目递减[6][7];
- 在第二列用英文字母
为结晶轨道的席对称性标序,最高席对称性被标记为
;
- 第三列为席对称性;
- 第四列和第五列分别为结晶轨道内位点的限制性坐标和 Miller 指数。
第一列和第二列的合并被称为 Wyckoff 位置。
在对给定空间群的 Wyckoff 列表中,第一行恒为基于恒等算符的一般点,其位点等效点的个数即为该点群的复合度(multiplicity);在大部分情况下最后一行总为经过原点而垂直于作图平面的
轴上点,其席对称性等于点群的对称性。
在席对称性中的中位点
是为了表明该席对称性的对称要素与点群对称要素的对应关系。比如下图中的
和
两个 Wyckoff 位置,其席对称性分别为
和
,意思是它们的席对称性中的对映面分别是点群记号
中的第二个和第三个对映面。
点群声明例题
说完了点群,让我们开始引入单个和多个平移对称算符,即进入到平面群和空间群的范畴。
向在结晶学范畴内合法的 32 种点群(point group)中引入平移对称性,分别用滑移镜射面(glide plane)和螺旋轴(screw axis)依次替换点群中的对称面和螺旋轴,即可在二维和三维空间中分别得到 17 种平面群(plane group)和 230 种空间群(space group)。
在向点群中引入平移对称性要素的同时也在产生新的对称元素。
对于任意实际存在的晶体结构,其必为 230 种空间群中的一种。
平面群(plane group)
The plane groups are obtained as the union of the translational symmetries of the 2D lattice with the point group symmetry about the lattice point when decorated with an atomic or molecular basis.
平面群的命名法即是将平面晶系的 Bravais 点阵符号 + 点群符号。
绘制平面群的基本步骤是
- 绘制其所位处的晶系;
- 在晶系内的每个节点内将点群置入;
- 寻找其他所有由于点群被引入而增添且隐含的对称要素。
平面群 例 1
以二维斜晶格(
,oblique lattice)为例,若以
点群修饰
二维晶系的每一个节点,即得到
平面群
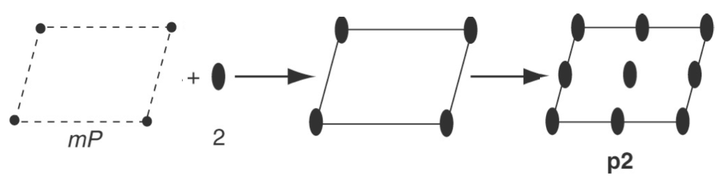
如上文所说,在引入平移对称性的同时会向系统中引入新的对称要素。在
平面群中,额外增加了位于形心和各边中点处的
重对称中心。以空心圆代表位于一般位置的物体,在
平面群中一般点具有无穷多个等效位点(equivalent point),但在每个晶胞内只具有 2 个。
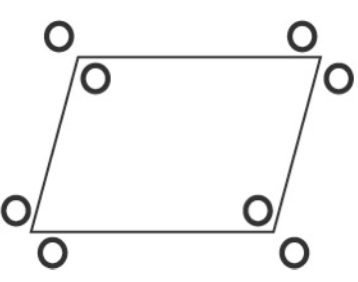
其席对称性位点为
。
平面群 例 2
向二维正方形晶格(
,square lattice)中引入
点群,得到
平面群。
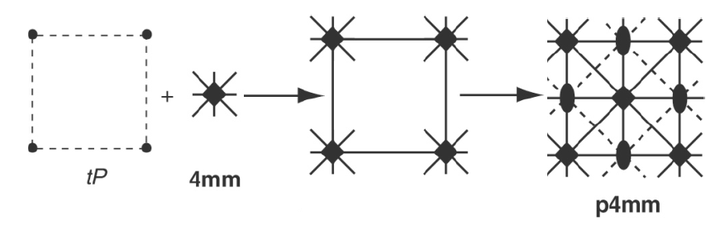
由于点群对称要素的引入,额外带来了位于各边中点处的
重对称中心、位于形心的
重对称性,和位于四个各边中点中的任意两点所确定的直线的滑移镜射。
对于任意一般位置点,其在晶胞内包含自身共有 8 个等效位点。
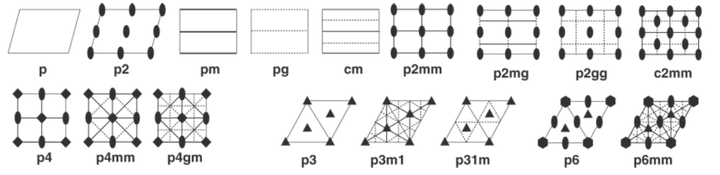
二维平面群共有 17 种,如下图所示。除旋转对称中心外,实线表示对映对称,虚线表示滑移镜射面对称。
空间群(space group)
空间群的操作本质与平面群类似。
空间群的命名法主要采用国际通用的 Hermann-Mauguin 记法,由大写的 Bravais 点阵的定心信息[
(
)centering information]+ 点群符号。
空间群的二维图示是俯视角度的底面,即平面
,晶系的
轴朝向作图平面的上方[8]。
空间群 例 1
向三维正交晶系素晶胞
中引入
点阵,得到
三维空间群。
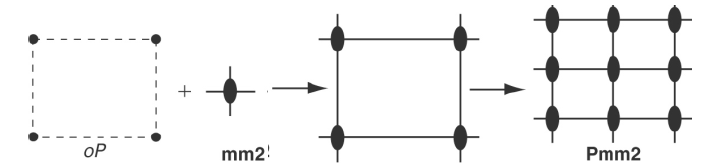
当对映面和不在平面上的平移矢
同时出现时,将在
处产生新的平行对映面。
在正交的两个对映面的交线处,将产生新的
重对称轴。
国际晶体学表(International Table of Crystallography)
在国际晶体学表(International Table of Crystallography)[9]中,
空间群的示意图如下图所示。
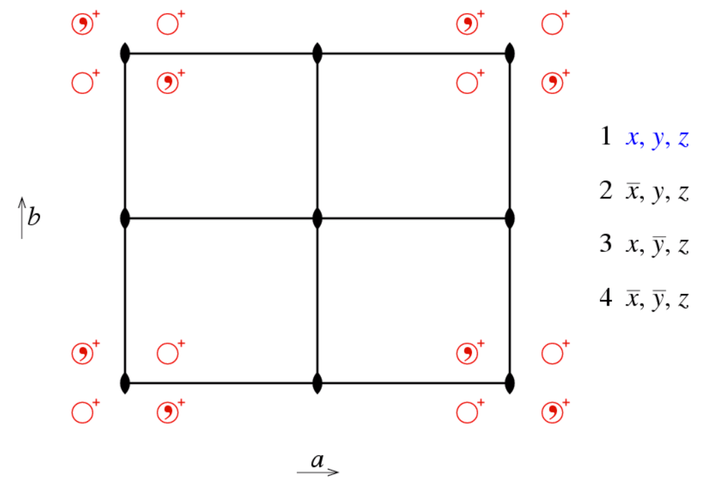
在国际晶体学表中,空心圆
表示位于原点附近的一个物体(object)/ 一般点(general point);正号
和负号
分别表示该一般点位于作图平面的上方和下方;分数符号
表示该一般点位于作图平面上方
晶胞单位处;内部带有逗号的空心圆意味着该一般点是原一般点经由瑕旋转得到的对映异构体。
空间群 例 2
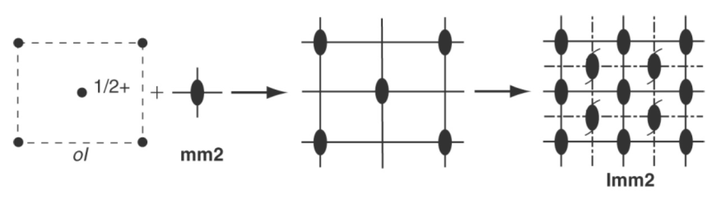
向体心正交晶胞
中引入点群
操作,得到三维空间群
。在图示中,位于中心的点实际上是
晶系的体心,其位于作图平面上方
个单位晶胞处,故被标记为
。
由此,除了基本的由于对映面与非共面平移矢的结合所得到的额外的诸平行对映面、和由于对映面的交线得到的额外的诸
重对称轴,在
及其对称等效处还得到了共计 4 个
重螺旋轴。
共形空间 / 非共形空间群 [(non-) symmorphic space group]
若一空间群记号种不包含螺旋轴和滑移镜射面的记号,即不包含平移元素,则称之为共形空间群(symmorphic space group);反之,称为非共形空间群(non-symmorphic group)。
共有 73 种共形空间群,其中 61 种可通过除螺旋和滑移镜射外的对称操作的结合得到,剩余 12 种需要添加额外操作。
共有 157 种非共形空间群,可通过滑移镜射或螺旋轴系统地替换一个或多个点群的 Hermann-Mauguin 记法中的对称要素得到。
空间群帮助研究者只需要利用最小数量的原子位置即可完备描述晶体结构、晶体的全部对称要素和蕴含的对称操作、并帮助研究者限制其宏观性质(restrict macroscopic properties)。
空间群计算例题
以上。

