这是个很适合用计算机来模拟的问题;
首先,我们回顾一下,光的入射角和反射角相等,在图形学中是怎么计算的;
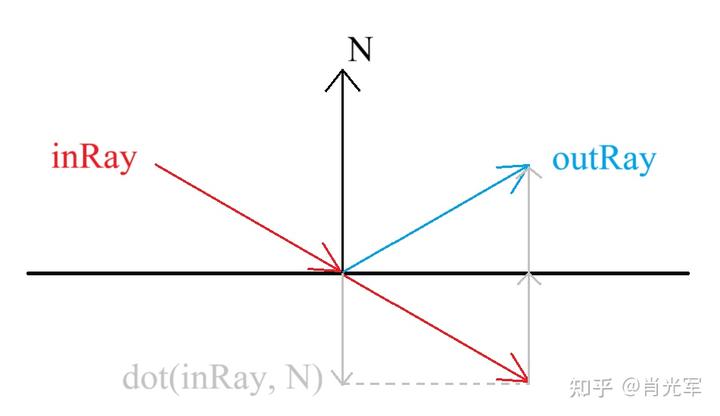
假设法线是 N,则我们可以先计算入射光 inRay 到法线 N 的投影长度 dot(inRay, N),然后再减去两倍法线投影长度的向量,就能得到反射光 outRay;
可以注意到这个算法是很简洁优雅的,且适用于任意 N 维向量(N >= 2),写成代码如下:
// 求镜面反射向量
vec3 GetReflectionRay(in vec3 inRay, in vec3 N)
{
float iDotN = dot(inRay, N);
return inRay - N * iDotN * 2.0;
}
那么如果入射角和反射角互余,该如何计算呢?

从图中我们可以看到,只要将入射光 inRay,沿着它与法线 N 组成的平面,往法线方向旋转 90° 角即可;
正好之前研究过简易的向量旋转计算,简略描述一下;
游戏开发过程中,经常会需要计算一个向量朝指定方向旋转给定角度;
通常这类需求需要每帧计算,UE 本身没有提供可直接调用的接口,转成 FRotator 调用 UKismetMathLibrary::RLerp 未免开销太大,且仍需要知道当前距目标方向的夹角(众所周知 ACos 比 Cos 开销大得多);
所以写了一个算法,直接计算旋转所需角度后的向量,尽可能减少计算开销,且可扩展到任意 N 维向量,原理如下:
将向量 A 往向量 B 插值,核心是计算 lerp(DirA,DirB,t) 中的 t 值,使其正好满足旋转的角度,通过相似三角形可以计算出插值后的 x 值,然后归一化就可作为返回结果 ResDir 了;
当然,这种计算是基于插值的,所以当两个向量正好反向(平角)时是无法计算的,数学上体现在分母为 0;
此时也无法确定要朝哪个方向旋转,二维上要考虑是顺时针还是逆时针,三维及更高维度则有无数个旋转平面,所以需要引入其他的方向参数,但在此只做简单计算不予考虑,可自行额外扩展方法。
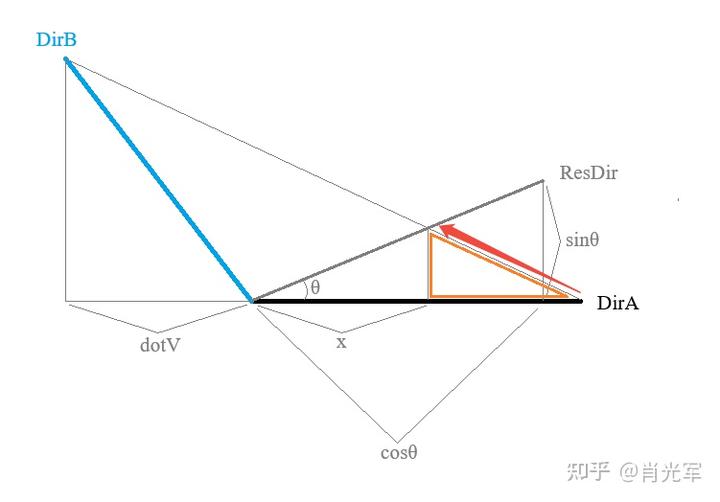
写成代码的话如下:
// 将向量 A 朝向量 B 旋转 theta 弧度
bool RotateVectorByRadian(in vec3 DirA, in vec3 DirB, float Theta, out vec3 ResDir)
{
ResDir = vec3(0);
float dotV = dot(DirA, DirB); // 求点积值
if (dotV <= -1.0f) { return false; } // A、B 为平角,非法
float cosT = cos(Theta), sinT = sin(Theta);
if (dotV >= cosT || dotV >= 1.0f) // 旋转的角度更大,或 A、B 同向,直接返回 B 的单位方向
{
ResDir = DirB;
return true;
}
float m = 1.0f / (dotV - 1.0f);
float k = sqrt(1.0f - dotV * dotV) * m;
float x = cosT * k / (cosT * k - sinT);
float resT = (x - 1.0f) * m;
ResDir = normalize(DirA + (DirB - DirA) * resT);
return true;
}
计算会比原本的反射要复杂一点,但好在也算简洁,且也可以拓展到 N 维向量;
其“平角无法计算”的特性也完美满足题目“除了垂直入射光被吸收外不违反光路可逆”的要求,则此时我们的反射代码如下:
// 求镜面反射向量
vec3 GetReflectionRay(in vec3 inRay, in vec3 N)
{
/*float iDotN = dot(inRay, N);
return inRay - N * iDotN * 2.0;*/
vec3 res;
RotateVectorByRadian(inRay, N, PI * 0.5, res);
return res;
}
替换了反射光的计算代码后,就可以直接渲染图片了;
但在这里先提一下,反射除了镜面反射外,还有漫反射,在计算机渲染中,一般是将漫反射当做粗糙平面,即法线并不总是垂直向外的,会将法线随机扰乱后,再来计算反射光线;
所以我们修改反射光的计算,可以同时应用在镜面反射和漫反射上!
下面是一个经典的方盒子渲染图,正常光线版;

下面则是互余反射版本;

再让小球动起来,渲染个视频,正常反射和互余反射对比如下:
 小球动 - 正常反射 https://www.zhihu.com/video/1955728966489964982
小球动 - 正常反射 https://www.zhihu.com/video/1955728966489964982  小球动 - 互余反射 https://www.zhihu.com/video/1955729129023448343
小球动 - 互余反射 https://www.zhihu.com/video/1955729129023448343
再加个摄像机动起来的,正常反射和互余反射对比:
 相机动 - 正常反射 https://www.zhihu.com/video/1955729338185000817
相机动 - 正常反射 https://www.zhihu.com/video/1955729338185000817  相机动 - 互余反射 https://www.zhihu.com/video/1955729438638604945
相机动 - 互余反射 https://www.zhihu.com/video/1955729438638604945
最后,只给个小球,估计看官老爷们肯定不满意,补个相对真实点的场景对比:


可以看到,由于漫反射的存在,光照大体还是正常的,在阴影和镜面反射的地方,异常会比较明显;
至于为什么办公室场景不加个视频渲染,电脑跑不动了…完结撒花~
9 月 30 日更新:
有很多人都说,球形在互余反射下看上去像圆锥,那圆锥看起来是啥样?
更新一波圆锥的正常反射:
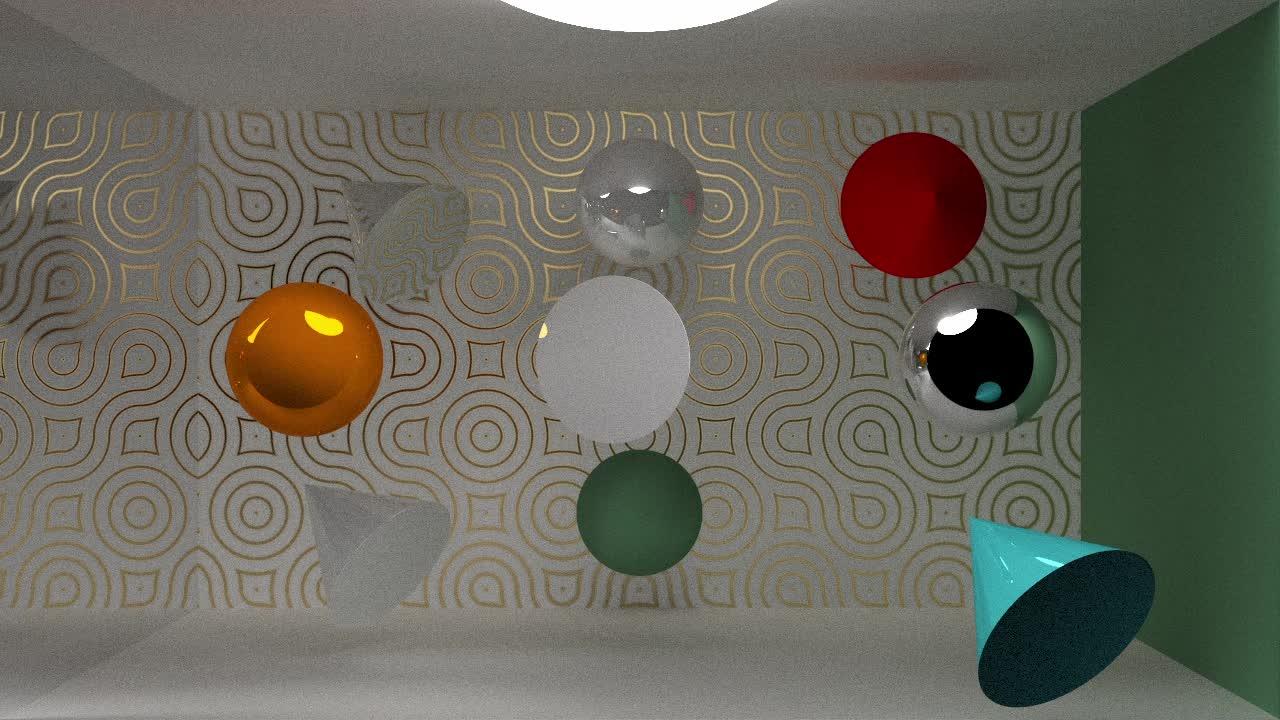 圆锥 - 正常反射 https://www.zhihu.com/video/1956295103393042670
圆锥 - 正常反射 https://www.zhihu.com/video/1956295103393042670
圆锥的互余反射:
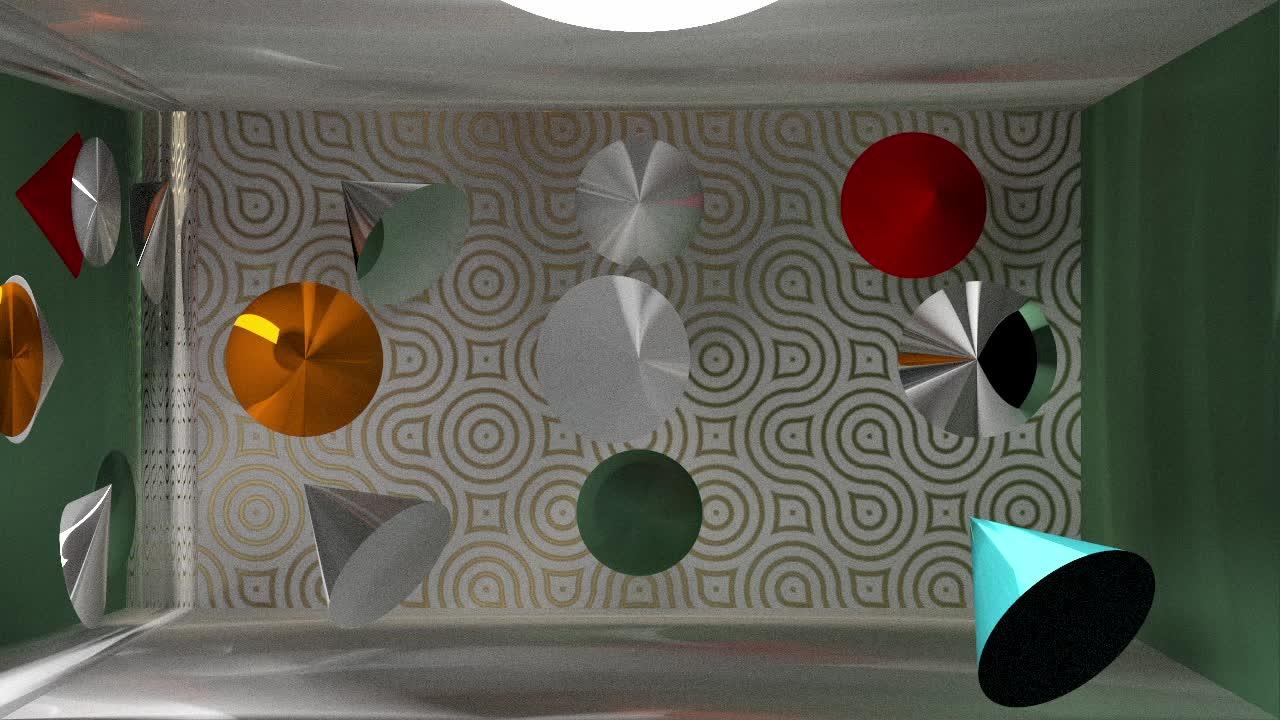 圆锥 - 互余反射 https://www.zhihu.com/video/1956295229205374513
圆锥 - 互余反射 https://www.zhihu.com/video/1956295229205374513
可以看到,在尖尖正对着相机的情况下会有些类似,但跟球形还是略有不同的;
