数学“男厕尴尬问题”如何求解?
谢邀,这是一个有趣且颇为典型的数学问题。
更专业一点来说,男厕尴尬问题本质上是一种分治递归(divide-and-conquer):
- 第一个人先占到一端;
- 为了和别人保持最远距离,第二个人自然会跑到厕所的另一端;
- 之后每次的新来者,实际上就是在剩下的区间里继续找一个中点,把原区间分为两个更小的独立子区间;
- 后续新来者的选择只会在各自子区间内部独立进行,而完全不用考虑其他子区间(因为跨区间的人只会相隔更远)。
这样一来,把思路捋清之后,原问题就可以用递归的思想来解决。把这个递归过程画出来,可以得到一棵近似二叉树的结构:根节点对应整排坑位,左右节点对应被分割出来的子区间,直到不能再放人为止。这棵树的深度和分支数就能决定最终容纳的人数
。
考虑到回答阅读难度,我将本回答分为两个部分,对相应内容感兴趣的同学可以选择性阅读:
- 科普性介绍:解释题述中「男厕尴尬问题」的背景和直观理解;
- 数学推导:给出
通式的求解过程;
一、什么是「男厕尴尬问题」?
相信不少人都听说过食堂就坐时的「洪特规则」和「泡利不相容原理」,在公共厕所里其实也有类似不成文的约定,也就是所谓的「男厕尴尬问题」。
这实际上源自生活中的小观察:
在公共厕所里,如果有一排小便池,大多数男性在选择时会本能地避开其他人,希望保持一定的安全距离。典型的约定就是相邻的坑位不能使用(否则会带来心理上的不适)。在此基础上,每个人还会尽可能选择离别人最远的位置。

于是,我们可以把这个社交距离抽象成数学规则。我们把这一排坑位编号为
,每次新来的人都要在空位中选择,简单来说就是:
- 规则一:不能与已有的人相邻;
- 规则二:使得「自己到最近的人的距离」最大;
- 重复下去直到坐不下为止,记此时人数为
。
如果你对这个问题尚未理解清楚,我们可以举几个特例来做说明。
首先
时显然只能有一个人占据坑位。而当
时,这些情况也都是 trivial 的,两个人分别占据这些坑位的两端,剩下的坑位都属于「无效坑位」(即不能再有人占据)。
那么我们要解决的就是
的情况。
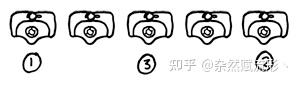
我们考虑
的一个特例来做说明,即某公厕里有一排 8 个小便池:
其中
代表空余坑位,接下来我们将用阿拉伯数字代表依次进入男性的编号。当第 1 人进入时,他会默认选择最边缘的坑位(我们在此约定默认选择 1 号坑位):
当第 2 人进入时,他自然会选择另一端,即 8 号坑位:
当第 3 人进入时,为了保证和前两个人相距尽可能远,他只会选择 4 号坑位或者 5 号坑位:
当第 4 人进入时,显然他只剩下一种选择,即占据另一侧的中点(6 号坑位或 3 号坑位):
之后便无法继续增加了,故最终只能容纳
人。所以实际上通过这个特例就能窥见解决该问题的关键:先占据两端,然后不断往区间的中点去填即可。
实际上这类依次占位置、保持不相邻的问题,在数学和算法里也很常见,比如电话问题、不相邻就座问题等,也都是有一点类似的味道在里面的。
二、计算 的通式
在此前我们已经对原问题做了大致的分析,得到了以下结论:
现在我们对
的情况进行分析:
- 第 1 个人占据 1 号坑位,此时 2 号坑位被禁止(因为不能与人相邻);
- 依前述规则二,第 2 个人在所有可选位置中会选择与第 1 个人最远的位置,也就是
号坑位,那么
号坑位也被禁止;
- 占据两端后,剩下的可用区间正好是连续的一段
,这个区间的长度是
。考虑下一次进入的第 3 个人,他会落在中间某个使到最近已有人的距离最大的点。一个容易观察到的事实是,第 3 个人占据的坑位要么是中线左侧的某个位置,要么是中线右侧对应的对称位置(这两种情况实际上是完全对称的),从而把剩余可用区间分为两部分(左子区间与右子区间)。把这一步看作是在
里选择一个划点把问题分为两半是自然的。
- 令
。那么就可以把
看作两个子区间,左子区间从 1 号坑位到
号坑位(长度为
),右子区间从
号坑位到
号坑位(长度为
)。此后的占据过程与分别在这两个子区间内部按相同规则放入的过程是等价的,且这两个子区间在之后的占据过程中互不影响,这是因为任何落在左子区间的新来者到右子区间所有已占人的距离都更大(或相等),所以左子区间内部的选择只由左子区间自身决定,右子区间同理。于是原问题就被分治为两个规模更小的问题。
- 注意到在相同规则下,左子区间能容纳的人数为
,右子区间能容纳的人数为
。但要注意两边都把位置
计入了一次,合并到原问题时应减去 1(避免重复计数)。
所以我们就可以得到如下分治递推关系式:
如果你看不惯这些取整函数(上述公式给出的是向上取整函数
,代表的含义是选择中间右侧的位置,如果使用向下取整函数
,代表的含义就是选择中间左侧的位置,这两者是完全对称的),可以把它改写成分段形式。
若
为偶数
,则
,
,那么
同理,若
为奇数
,则
,
,那么
结合我们前面给的初值条件,那么现在的问题实际上就转化成了一个数列问题,我们要求解的正是
的通项公式。
这个数列求解起来说难也不难。前人对于这一系列问题研究的已经很透彻了,比如 Wundling, S.[1]和 Hwang, Hsien-Kuei & Janson, Svante & Tsai, Tsung-Hsi.[2],这两篇论文都有详细介绍(不过可惜的是前者是一篇德语论文……)
但说简单也并不简单,解决这个问题的关键在于观察到递推在以 2 为基底的尺度上出现层级结构(也就是每次把
缩小大约一半),所以
的增长规律和二进制展开有很强的关系,所以我们把
写成
其中
。这一步实际上是把
分解为最高的二进制位
+ 剩下的余数
,这样我们就可以按
落在哪个区间
来分段讨论,也就是按照
为归纳变量来进行归纳证明。
现在我们期待证明
或者等价地
为简便起见,记
,则
。且记
,
,那么我们的递推关系就可以写成:
我们可以根据
的奇偶情况把
具体表示出来,
若
(偶数),则
,所以
若
(奇数),则
,所以
综上,有
值得注意的是因为
,所以
,因此
(这一步很重要,这说明
对应的层数是
,而前面我们论证过了
对应的层数是
)。
同理,若
奇,则
与上述讨论一致。若
偶,则
,所以
的阶数要么是
,要么是
(
)。
因此我们可以把归纳假设应用于
与
。而根据
的形式,我们需要证明两部分:
- 平台段:若
(也即
),则
;
- 线性段:若
(也即
或
),则
。
接下来我们逐一证明。
2.1 平台段
在前面我们得到了
,可以把
的层数视为
,按照归纳假设对应的
给出
再看
:
若
奇,则
,
。
若
偶,则
。因为
(若
,
,这是唯一可能使得
的情况),我们需要把
分为两小支进行讨论:
- 若
,则
的内部余数(相对于
)属于
。按照归纳假设同样可以得到
。
- 若
(即
,此时
,这是一种边界情况),则
,此时
对应的层数是
(而非
),可得
此时仍有
。于是无论
奇偶,在
的范围内,我们都有
综合
和
的结果,我们可以得到
这正是平台段中我们需要证明的结论。
2.2 线性段
此时
的内部余数
满足
,按照归纳假设对应的
我们可以得到
再看
,方法和 2.1 节是一致的:
若
奇,则
,
;
若
偶,则
。由于
,同样有两种可能:
- 若
则
,按归纳假设
(即
也处在线性段);
- 若
(这是边界),则
,同样可以得到
。
综上在
下,总有
综合
和
的结构,我们可以得到
这正是线性段中我们需要证明的结论。
将
和
的结论整合在一起,我们就能通过归纳法得到结论
,即对所有
,都有:
Q.E.D.
这样我们就通过一套繁琐的讨论证明了
的通式。
这个结果看似复杂,但理解起来其实并不困难。其中
就正好代表最初那个站在末端的人,而第二项表示经过
次分把区间分半、在每个子区间放一个人的操作,会把原区间分成大约
个小段(或产生
个能被占的坑位),所以有
个坑位必然被占据(不依赖于余数的具体细节)。第三项的
函数实际是为了把两段行为统一起来:在某个区间
保持平台常数;当
足够大时,额外的每增一个坑位就能立刻带来 1 个额外的人,直到进入下一层级为止。
通过画图我们也能直观地看出这一点,随着坑位的增加,能容纳的人数
出现明显的阶梯式增长的情况,而且还具有自相似性:
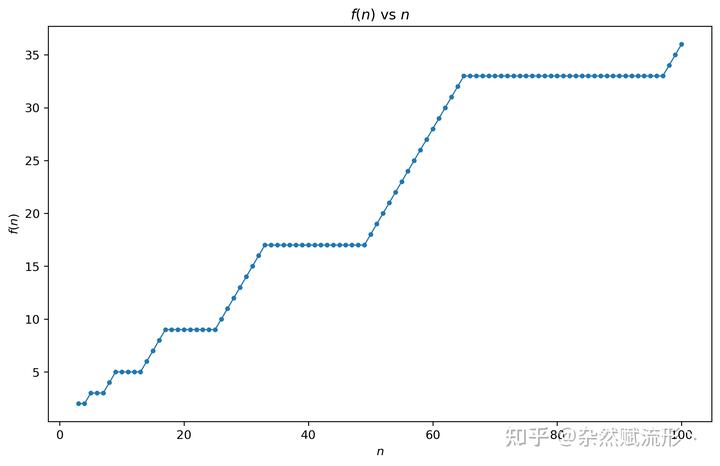
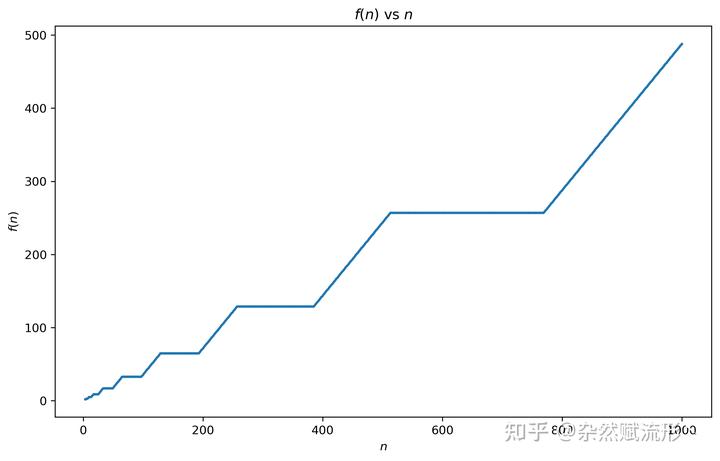
同样你还可以进一步画出厕所利用率
随着坑位
增长时的变化情况:
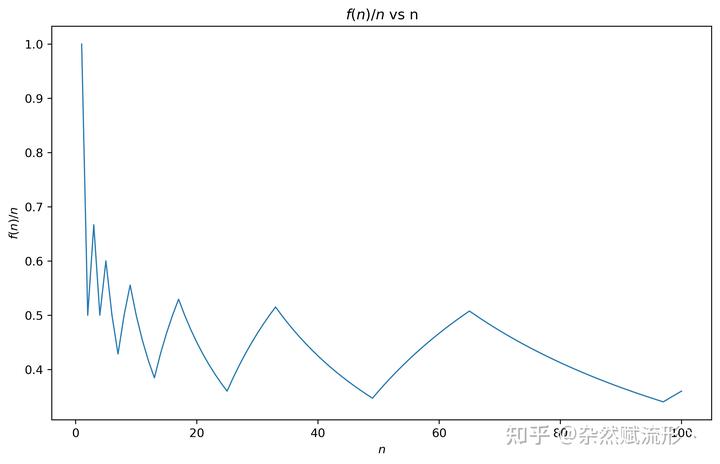
如果厕所设计者设计时,兼顾考虑到「男厕尴尬问题」与厕所利用率,那么最佳的坑位数应当选取
另一方面,如果设计者完全不懂数学,那么他有可能倒霉地设计了厕所利用率最低的情况,即最差的坑位数为
数学,真有趣!

