纵观数万年的人类文明史，这样的问题实在寥寥。

1. 阿基米德群牛问题（Archimedes's cattle problem）

• 提出到解决：至少 2200 年

提问者已不可考，但阿基米德于公元前 3 世纪下半叶在论著《群牛问题》中记载了本问题。原文是 22 组对句组成的诗句：

朋友，如果你自认为还有几分聪明，请来准确无误地算一算太阳神的牛群，
它们聚集在西西里岛，分成四群悠闲地品尝青草。
第一群象乳汁一般白洁，第二群闪耀着乌黑的光泽。
第三群棕黄，第四群毛色花俏，每群牛有公有母、有多有少。
先告诉你各群的公牛比例：白牛数等于棕牛数再加上黑牛数的三分之一又二分之一。
此外，黑牛数为花牛数的四分之一加五分之一，再加上全部棕公牛。
朋友，你还必须牢记花牛数是白牛的六分之一又七分之一，再搭上全部的棕色公牛。
但是，各群的母牛都有不同的比例：
白色的母牛数等于全部黑色公母牛的三分之一又四分之一。
而黑母牛又是全部花牛的四分之一加上五分之一，请注意，母牛公牛都要算进去。
同样的，花母牛的数字是全部棕牛的五分之一加六分之一。
最后，棕色母牛与全部白牛的六分之一加七分之一相一致。
朋友，若你能确切地告诉我这些公牛母牛膘肥体壮、毛色各异，一共有多少聚集在那里，你就不愧为精通算计。
但你还称不上聪明无比，除非你能回答如下的问题：
把所有的黑白公牛齐集一起，恰排成正方形，整整齐齐。
辽阔的西西里岛草地，还有不少公牛在聚集。
当棕色的公牛与花公牛走到一起，排成一个三角形状。
棕色公牛、花公牛头头在场，其他的牛没有一头敢往里闯。
朋友，你若能够根据上述条件，准确说出各种牛的数量，那你就是胜利者，你的声誉将如日月永放光芒。

看起来复杂冗长，如果把他写在我们的数学试卷上，应当是这样的画风：

西西里岛的大草原有群牛，按毛色分成 4 组：乳白牛、黑牛、黄牛和花斑牛。每组中的公牛数占大多数，它们之间的关系满足：

1、白公牛=黄公牛＋（1/2＋1/3）黑公牛
2、黑公牛=黄公牛＋（1/4＋1/5）花斑
3、花斑公牛=黄公牛＋（1/6＋1/7）白公牛
4、白公牛=（1/3＋1/4）黑牛
5、黑公牛=（1/4＋1/5）花斑公牛
6、花斑公牛=（1/5＋1/6）黄牛
7、黄公牛=（1/6＋1/7）白牛

• 第一小题：求各个牛的数量
• 第二小题：加入以下两个条件，求各个牛的数量：

白公牛＋黑公牛＝ 一个平方数
花斑公牛＋黄公牛＝ 一个三角数

第一小题比较简单，其实就是个多项式求解的问题

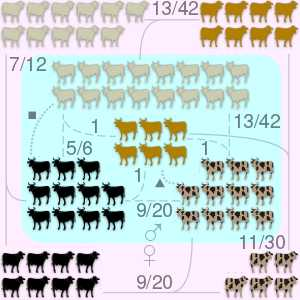
把题目内括号里的分数相加后列个方程：

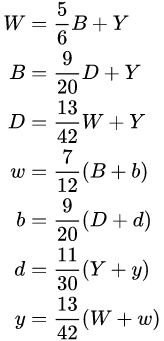
初一下学期的同学一看，咦？这题我也会啊，不就是二元一次方程组的升级版吗！

不错，这就是个普通的多元一次方程组而已，只不过未知数比较多，比较废草稿纸而已。如果你有足够的耐心和纸，那么经过大量重复枯燥的消元运算并且还不出错的话，可以得到以下最小整数解：

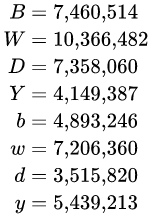
最小整数解换句话说，就是第一小题有无数个解。以上解的所有整数倍解都是问题的解。

如果你能解决第一小题，先不要得意忘形，因为诗中只说了这仅仅只有“几分聪明”。

人类第一次给出第一小题的答案是在 1773 年，之所以这么晚发现是因为这本书在近千年时间里都被尘封，没人注意到。

德国著名作家莱辛（Lessing）在图书馆读到这个问题后，把它拿给一位数学家朋友看，这位朋友还算给力，很快就算出了这个答案。

然而真正丧心病狂的是第二小题。

由阿基米德的算术论著《数沙者》大概能看出他在大数上有着超越时代的造诣，他是已知宇宙中第一个给出宇宙中沙子总数量估计的生物（他估计出了个 63 位数）。

现在的我们可以轻松估计出宇宙中行星的数量是个 24~26 位数，一颗行星上沙子的数量介于 18 位~28 位数之间。因此宇宙的沙子是个 42~54 位数。

但考虑到公元前 3 世纪人类对宇宙的了解水平，阿基米德能做出这种准确度的估计实属惊为天人。

也许是凭借着这份天赋，他相信最终解的值将会很大，于是他将此问题留给了后人。

我们再来看看第二小题的条件：

1. W+X ＝ 一个平方数
2. Y+Z ＝ 一个三角数

平方数很好理解，就是整数的平方，能够整齐排成正方形；（1，4，9，16。。。）

三角数就是能整齐排成正三角形的数：（1，3，6，10。。。）

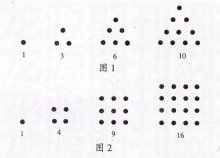
问题理解起来不难，无非就是把第一小题的解不断翻倍，从中找出同时满足 W+X=平方数和 Y+Z=三角数条件的解。

然而这个数如此巨大，以至于在莱辛公布这个问题的 100 年内，一直没人能给出答案。在那个没有计算机的年代，不知道废了多少草稿纸，多少脑细胞，多少头发。。

直到 1880 年，德国数学家 Amthor, A. 和 Krumbiegel B. 在他们发表的论文《Das Problema bovinum des Archimedes.》^[1]中给出最终解第一个估值：W，即黄公牛的数量是 1598*10^206541

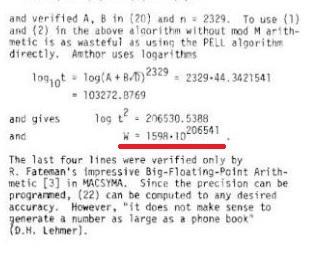
牛总数为

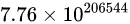
这是一个巨大的数字，高达 206545 位，天文数字在它面前也不值一提，这么多的牛，可观测宇宙都放不下，不愧是“太阳神的牛群”。两位数学家在论文中吐槽：“我把一个能把电话本都写满的数字全部计算出来没什么意义吧”。

另外，这个数字只是第二问的解中的最小值，还有很多比这个数字大的多的解。

尽管给出了答案，但这还没有达到原诗要求的“准确无误”。

1889 年，美国伊利诺伊州的一位土木工程师和他的 2 位朋友组成了希尔斯伯勒数学俱乐部，决定计算出剩下的那些数字。经过 4 年的努力，他们计算出了前 32 位数和后 12 位数^[2]。靠近两端的数是计算难度最低的，就算他们能够以同样的速度给出中间的数字，也需要 18,776 年才能给出精确答案。更可惜的是，后人证明他们算的数都弄错了。

正如诗中所述，在没有计算机的情况下，还能“准确无误”解出问题，那真是“如同日月永放光芒”了。

1946 年，世界上第一台通用计算机“ENIAC”于美国宾夕法尼亚大学诞生。

1965 年，这个问题得到终结：终结者是滑铁卢大学的Hugh C. Williams, R. A. German, Charles Robert Zarnke 和两台超级计算机（IBM 7040 和 IBM 1620）^[3]。两台超算相互合作花了 7 小时 49 分钟的运算时间，才在 42 张 A4 纸上打印出了这 206545 个数字^[4]。

2. 尺规作图三大上古难题2.1 倍立方

• 提出到解决：约 2266 年

问题的来源可追溯到公元前 429 年。传说中，一场瘟疫袭击了希腊提洛岛（Delos），造成四分之一的人口死亡。岛民们去神庙请示阿波罗的旨意，神谕说：要想遏止瘟疫，得将阿波罗神殿中那正立方的祭坛加大一倍。人们便把每边增长一倍，结果体积当然就变成了 8 倍，瘟疫依旧蔓延；接着人们又试著把体积改成原来的 2 倍，但形状却变为一个长方体……第罗斯岛人在万般无奈的情况下，只好鼓足勇气到雅典去求救于当时著名的学者柏拉图。

开始，柏拉图和他的学生认为这个问题很容易。他们根据平时的经验，觉得利用尺规作图可以轻而易举地作一个正方形，使它的面积等于已知正方形的 2 倍，那么作一个正方体，使它的体积等于已知正方体体积的 2 倍，还会难吗?

这个问题也相当于在问：尺规作图能否作出长度为单位长度

倍的线段？

与倍立方问题相比，倍平方问题要简单得多。给定一个单位长度的线段，只需做一个以它为边长的正方形，以正方形的对角线为边长的正方形，面积就是 2。 也即是说，尺规作图可以作出长度为单位长度的

倍的线段。然而，

和

虽然相似，却有本质区别。直到 1830 年，埃瓦里斯特·伽罗瓦提出群论后，这个问题才有望得到解决。

1837 年，法国数学家Pierre Wantzel给出了严格证明。

证明方法是根据伽罗瓦的群论给出了规矩数的定义：能用尺规作图画出的所有线段的长度的群。

他进一步给出证明，一个数要满足规矩数，他必须是幂次为 2 的有限多项式。

每次尺规作图的步骤，都可以看成是一次运算，整数倍加减乘除，平方根运算都可以被尺规作图实现。但是，尺规作图所能实现的运算是有限制的。因为运算方法有限，即使运算的所有结果的总数能达到无限大，这个无限大也不包含所有的实数（类似偶数不包含所有整数）。

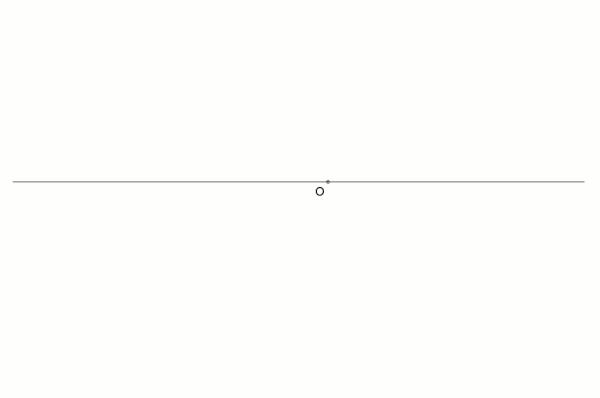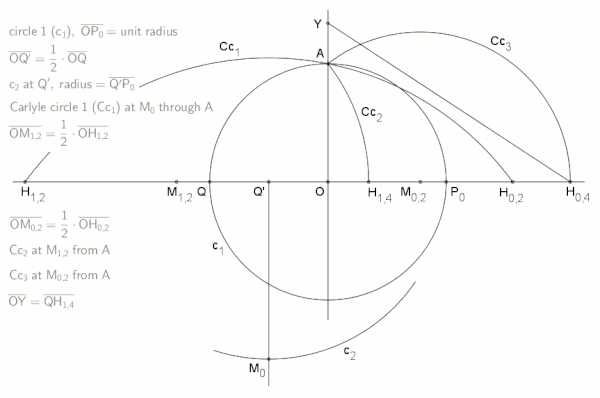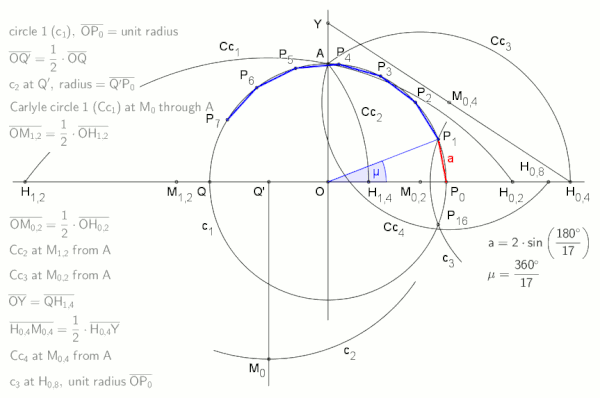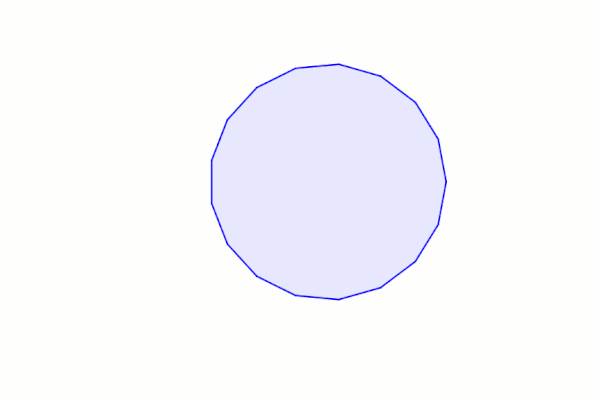
之所以高斯能尺规作出正 17 边形，正是因为 cos(2π/17) 能写成有限步的加减乘除平方根运算：

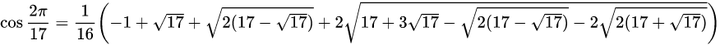
而倍立方问题是指已知单位长度 1，要作出

的长度。

然而，

的最小多项式是：

阶数 3 不是 2 的幂次。所以，用尺规方法无法作出一个立方体，使得它的体积是已知立方体的两倍。

（方便大家看懂，说的不是很严谨，准确的说是域扩张

）

2.2 化圆为方

• 提出到解决：至少 2296 年

问题和倍立方类似：尺规作图能否作出长度为

的线段？

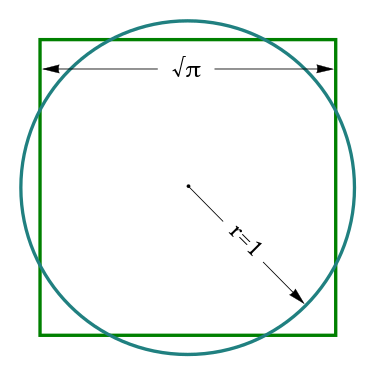
公元前 414 年，当时阿里斯托芬的戏剧《鸟》首次上演。在其中，雅典的梅顿（Meton）提到了化圆为方，似乎是为了讽刺当时他乌托邦的城市。

但丁(1265-1321)《天堂》，第三十三章，第 133-135 行：

As the geometer his mind applies
To square the circle, nor for all his wit
Finds the right formula, howe'er he tries

大致意思是，一个几何学家无论如何尝试也是找不到化圆为方的正确公式的。

但丁认为，化圆为方代表一项超出人类理解能力的任务，他将其与自己无法理解天堂相提并论。

毕竟那个时候π的精确值仍然停留在祖冲之的成果上。

1742 年，当 Alexander Pope 出版他的 Dunciad 的第四本时，化圆为方的尝试被视为“狂野而徒劳的”

Mad Mathesis alone was unconfined,
Too mad for mere material chains to bind,
Now to pure space lifts her ecstatic stare,
Now, running round the circle, finds it square.

1798 年，19 岁的高斯尺规作出十七边形，这是当时人类历史上最接近化圆为方的操作。高斯也认为是得意之作，要求将十七边形刻在自己墓碑上。据说后来还是被雕刻墓碑的人拒绝，因为觉得十七边形和圆太像了。

1761 年，Lambert 用以下的公式证明了π是个无理数：

Lambert 给了当时妄图精确计算出π精确值的数学家们一个暴击。

这下，化圆为方变得更加遥不可及了。

尽管Pierre Wantzel 1837 年严格证明了尺规作图的局限性，并给出了规矩数的范围。但是当时并没有人能证明圆周率是否属于规矩数。π是无理数并不能代表π不是规矩数，反例就是

这个问题的解决还需要证明圆周率的超越性。

超越的意思是：这个数无法表示成代数方程的根。即 不可能满足任何一个系数为整数的方程 ： 。打个比方， 是一个无理数，但不是一个超越数。因为 这个方程的一个正数解就是 。如果一个数无理但是不超越，我们虽然找不到它的精确值到底是多少，但是我们可以找到一个和它相关的方程来分析这个数的性质和特点。

从上面的描述，我们可以轻易看出，超越数必定不属于规矩数；如果能证明圆周率是超越数，那么就能终结这个两千年的问题。

1844 年，超越数由法国数学家 Joseph Liouville 首次提出。

1882 年，Ferdinand von Lindemann 等人证明了圆周率是超越数^[5]。由此，人类终于确认化圆为方不可能。

这个证明比较复杂，可以参考这篇文章：π超越性的 2 个证明 - 知乎 (zhihu.com)

证明一个数是不是超越数真的超级难，π是超越数，e 是超越数，但是我们至今也不知道π+e 是不是超越数。

1897 年，美国一位业余的数学家试图让印第安纳州议会来通过一项印第安纳圆周率法案，希望以法律的形式强制规定π=3.2 来逆天改命。最终，该法案被印第安纳州众议院表决全票通过，但是被参议院否决了。

2.3 三等分角

• 提出到解决：至少 2000 年

三等分角与化圆为方及倍立方问题并列为尺规作图三大上古难题。

问题是：能否仅用尺规作图法将任意角度三等分？

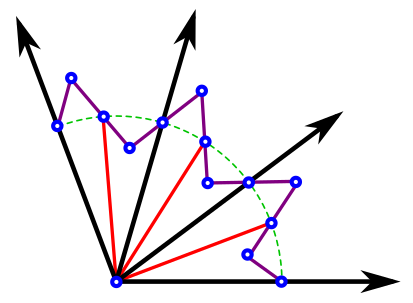
古希腊学者发现，尺规作图二等分角轻而易举，于是想推广到三等分。

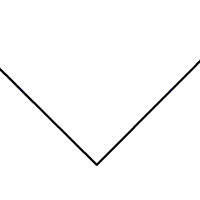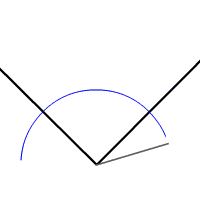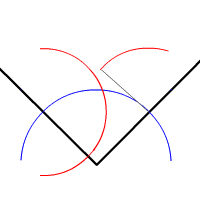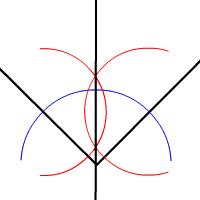
尽管有许多基于平面几何的论证和尝试，然而全部失败。和大家预料中的一样，这个问题也需要群论才能解决。

还是等到了 1837 年，三等分角被法Pierre Wantzel严格证明不可行（根据三倍角公式

中有个三次幂，证明方法和倍立方类似。）

3. 丢番图方程问题

丢番图方程，又称不定方程，是未知数只能使用整数的整数系数多项式等式；即形式如

的等式。

勾股定理、佩尔方程、四平方和定理和费马大定理都是一类丢番图方程。

丢番图是第一个在代数中引入符号的数学家，因此方程由他名字命名。他希望能找到一种算法，用来求解丢番图方程。

丢番图方程一般情况的可解答性问题

• 提出到解决：约 1700 年

这个问题不同寻常的难，困扰了人们数千年。

希尔伯特于 1900 年在巴黎的国际数学家大会演说中，用严谨的数学语言表达了这个问题：

对于任意多个未知数的整系数不定方程，要求给出一个可行的算法，使得通过有限次运算，可以判定该方程有无整数解。

并将其放入大会中23 个重要数学问题的第十题。

这个问题难就难在不知道从什么地方入手。尽管有无数人尝试，但是没有任何一个可靠的方法论。

直到图灵机概念的出现，计算机和可计算性理论的发展，数学家们才得以入手这个问题。

1970 年，尤里·马季亚谢维奇证明不存在任何算法，可以计算一般丢番图方程的整数解。甚至，在任何相容于皮亚诺算数的系统当中，都能具体构造出一个丢番图方程，使得没有任何办法可以判断它是否有解。

费马大定理

• 提出到解决：365 年

虽然没有达到千年，但考虑到其知名度以及它实际上也是丢番图方程的一个简单特殊形式，还是稍微提一下。

尽管只是个简单特殊形式，但其难度不亚于一般情况并且比一般情况晚了 24 年才解决。

一般来说，探讨一个命题的特殊情况要比探讨一个命题的一般情况要简单（那种暴力穷举的除外），而费马大猜想就是个经典的反例。

考虑丢番图方程的一个简单特殊形式：

aⁿ+bⁿ=cⁿ

当 n 为 1 时，只需要小学水平就知道方程有无数个解；

当 n 为 2 时，只需要勾股定理就知道方程有无数个解；

当 n 为 3 时，这个难度就已经超过大多数人的想象了；

1637 年，著名业余数学家费马在阅读丢番图《算术》拉丁文译本时，曾在第 11 卷第 8 命题旁写道：将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次的幂分成两个同次幂之和，这是不可能的。关于此，我确信我发现一种美妙的证法，可惜这里的空白处太小，写不下。

此时费马大定理被称为费马大猜想。

1770 年，欧拉证明 n=3 时定理成立。^[6]

1825 年，高斯和热尔曼同时独立证明 n=5 时定理成立。

费马大猜想提出之后的二百年内，对很多的特定的 n，费马大猜想都被证明正确。但对于一般情况，人们仍一筹莫展。

1908 年，德国人“保罗·弗里德里希·沃尔夫斯凯尔”宣布以 10 万马克作为奖金奖给在他逝世后一百年内，第一个证明该定理的人，吸引不少人尝试并递交他们的“证明”。

沃尔夫斯凯尔成立了沃尔夫斯凯尔委员会（Wolfskehl committee）后，收到数千个不正确的证明，所有纸张叠加超过 3 米^[7]。仅在第一年就有 621 个证明，到了 20 世纪 70 年代，各家证明方法的提出已经降至每个月大约 3-4 个。根据沃尔夫斯凯尔委员会评论家施里希廷（F. Schlichting）的说法，大多数证明都是基于学校教授的基本方法，并且提交证明的人大多“有技术教育但职业生涯失败”。用数学历史学家霍华德·伊夫斯的话来说，“费马大定理在数学里有一个特殊的现象，即在于它是错误证明数量最多的数学题。

这和今天想证明哥德巴赫猜想的人潮完全有得一拼。

1983 年，格尔德·法尔廷斯证明：对于给定的整数 n>2，至多存在有限组互素的 a,b,c 使得 aⁿ+bⁿ=cⁿ 成立。

费马大猜想最后于 1994 年由安德鲁·怀尔斯解决。

怀尔斯证明费马大定理的过程亦甚具戏剧性。在不为人知的情况下，他在七年里得出证明的大部分；然后于 1993 年 6 月在一个学术会议上宣布他的证明，并瞬即成为世界头条。但在审查证明的过程中，专家发现一个极为严重的错误。怀尔斯和泰勒之后用近一年时间尝试补救，终在 1994 年 9 月成功，这部分的证明与岩泽理论有关。他们的证明刊在 1995 年的《数学年刊》（Annals of Mathematics）之上。

这几个问题无一例外都和古希腊有关，从历史的角度看，古希腊不愧为哲学和现代科学的摇篮。不光是解决问题的人，提出这些问题也值得称赞。为了解决这些问题，发展出了多个全新的数学思想。横跨千年，播下文明的种子，激励人类不断攀登着数学大厦，驱动文明在知识的海洋里启航。