注:所有的更新均附在答案的末尾。
------------------
最近刚刚看到一个非常有趣的关于经典力学的悖论,这里分享一下。
之所以感到特别有趣,是因为它非常令人意外:我本来觉得经典力学那么清晰,那么确定,并且几百年的理论,该有的“悖论”应该早就被挖掘出来了吧,但是一个非常简单的思想实验告诉我,即使是经典力学这种几百年历史的如此经典的理论框架,仍然会有意想不到的东西突然跳出来击中你的脑洞。
这个悖论是匹斯堡大学的物理哲学家 John D. Norton 在 2003 年提出的,叫做“诺顿穹顶”(Norton's dome)[1],有时候也会被称为“the dome”。
Norton 本人提出这个悖论的初衷是想展示,即使是在经典力学中,也存在着不确定性。这种不确定性和混沌现象本质不同:混沌现象仍然是决定论的,只不过是在现实中我们不可能做出有效的预测。而 Norton 的这个思想实验想说的是,经典力学中,存在着原则上的不确定性。
我们想象一个拱顶的形状(就像是一个倒扣的炒锅),在这个拱顶的正上方放置着一个质点。如果这个拱顶绝对光滑,那么这个质点我们知道,是处在一个不稳定平衡的状态。也就是说,在理论上,它可以永远地呆在那里,保持静止。但是,实际上,任何一个微小的扰动都会打破这个平衡,使得质点沿着拱平面滑落下来。图片来自 Norton 的网页,以下未经标注的图片均来自同一出处。[2]
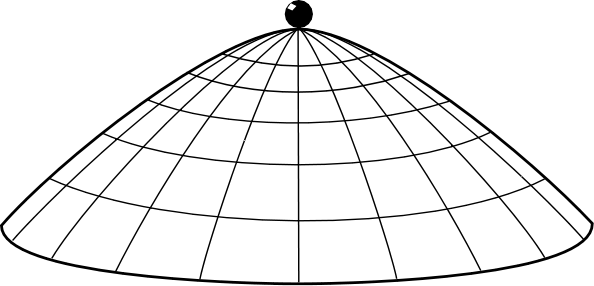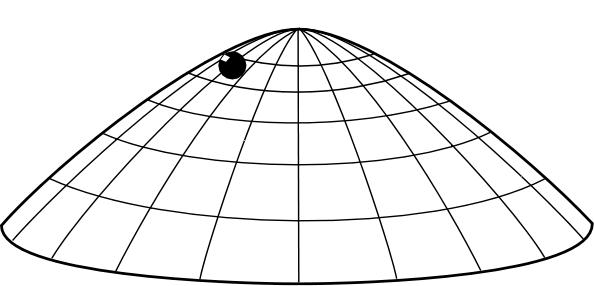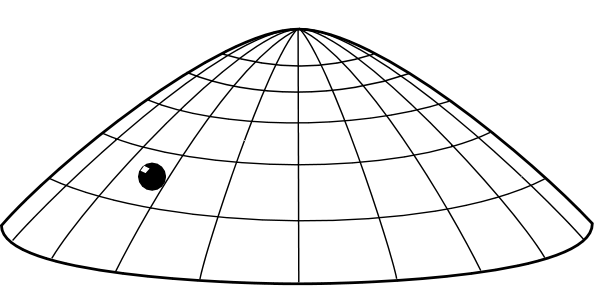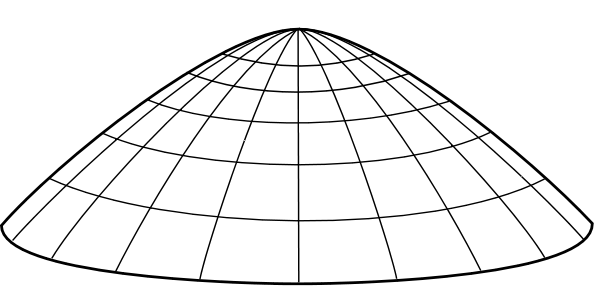
这个,就是混沌现象中最典型的“蝴蝶效应”,也就是说,小球的未来轨迹对初始条件极其敏感(但是请注意,这个现象虽然有蝴蝶效应,但并不属于混沌现象,因为它不具备混沌现象的另一个特征:拓扑混合性)。
但是,不论如何,这是一个严格决定论的现象,如果我们精确地确知初始条件,我们会精确地预测小球的未来运动轨迹。一个特例就是,如果小球被恰好放置在顶部,那么运动方程会告诉我们,它将会永远呆在那里,保持静止。它不会自发地滑落 —— 除非受到了某种扰动。
是这样吗?Norton 问。
他设计了一种特殊的拱顶。这个拱顶是这样的形状:
我们用两个坐标来描述它的三维形状(它中心轴对称),一个是滑动过程中下落的高度 h,另一个是沿着曲面下滑的距离 r(测地线长度):
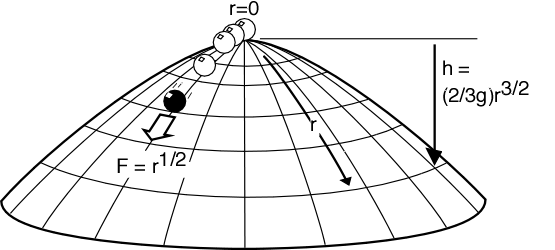
这个曲面就可以用这个方程来表示:
这个小球在滑落过程中,只受到重力的作用。那么,我们很容易得到,重力在沿着曲面轨迹的方向上的分量就是:
所以,我们可以根据牛顿第二定律列出动力学方程
我们再加上初始条件,在 0 时刻小球静止地呆在穹顶,就很容易解出这个微分方程。很显然,r=0 是这个方程的一个解。
但是,请注意这个方程在 r=0 的时候其实并不满足 Lipschitz 连续性条件,也就是说,它的解的唯一性并不被保证。也就是说,它可能存在多解。事实上,的确存在另外的解,例如说:
我们可以对它做出验证,确实如此。
那么,我们现在就得到了两类不同的解。第一类是完全规规矩矩地符合我们直觉的情况,它和其它的拱顶情形都完全一致:小球在顶部保持着微妙的平衡,一直静止下去。
而第二类解就显得非常诡异了。在这类解里面,出现了一个很随意的参数 T。这个 T 是可以任意指定的。也就是说,这个小球很随意地在顶部呆了一段时间(T),然后又毫无理由地滑落了。从数学上讲,这个 T 是完全任意的,所以,小球似乎完全任意地停了一会儿,然后就决定不再继续呆着了。至于它为何会突然滑落?没有任何突发的外力让它这么做,所以它的这个行为似乎是完全没有原因的。
那么理所当然,它似乎也就是完全非决定论的。
对于物理学中的不确定性,我们通常会用概率来描述它。然而在这个问题中,它似乎连概率都失效了。因为 T 是完全任意的,我们会想要给它指定一个完全均匀的概率分布 —— 然而它又是分布在整个实数域的,乃至于我们没有办法对这个分布做归一化。
这个悖论极其诡异。
首先,它太简单了,简单到几乎不需要什么计算。
其次,它的处理过程似乎和我们一般的物理学的计算有些格格不入。我第一眼看到这个悖论的时候,我的第一印象就是,这中间肯定有什么问题。但是找了半天,又总是似是而非,找不到问题到底是出在哪里了。
问题出在拱顶的顶部的奇异性吗?(我们可以看到,在顶部,其二阶导数是不连续的)。但是,牛顿定律难道不适用于特殊形状的边界条件吗?
问题出在 T 时刻吗?为了追根求底,我计算了在 T 时刻的各阶导数:
我们看到,在质点开始下落的瞬间,它的确是有零速度和零加速度。但是,它的四阶导数却不是零(加加加速度)。也就是说,质点在顶部一直以完全静止的状态,在下落前的一瞬间突然出现了一个加加加速度的阶跃。然而物理定律中并没有直接关于加加加速度的关系,因此这似乎也并不违背任何物理定律?
但是想一想似乎又有些问题:牛顿第一定律说,在外力为零的时候,质点保持运动状态不变。保持运动状态不变,是意味着速度的各阶导数均为零吗?还是只意味着加速度为零?
反正,这个悖论挺好玩的,暂时我还没有想到一个特别有说服力的驳斥。所以,我想用一句用滥了的结尾,“各位对此有什么想法,欢迎在评论区发言哦!”
更新 2022-8-10:
评论区中有一些讨论,个人认为有的有道理,有的则是完全误解了这个悖论。
请注意,这里讨论的是经典力学的理论中是否会自发出现不确定性的问题。也就是说,这是一个理论框架的问题,而不是一个现实的问题。我们讨论的是一个理论的特征,而不是物理现实的特征。这一点一定要分开。所以,那些说模型不符合现实,或者说做个实验验证的,其实都跑题了。
这里的数学原因其实非常清楚,但凡是学过微积分上册的人都知道,就是不满足 Lipschitz 连续性条件的,都无法保证其解的唯一性。在拱顶处二阶导数的发散,其实是导致这个悖论的数学原因。但是我们现在并不是在讨论数学问题,而是在讨论这种数学问题对一个物理模型来说意味着什么?事实上我们可以构造出各种任意的力场来使得动力学方程出现各种奇怪的解,但是这个悖论的聪明之处在于,它构造了一个看似非常物理的情形。我们不需要任何奇怪的力场,也不需要什么奇特的曲面。这个曲面其实非常容易构造出来。我们可以找到它的解析图形:
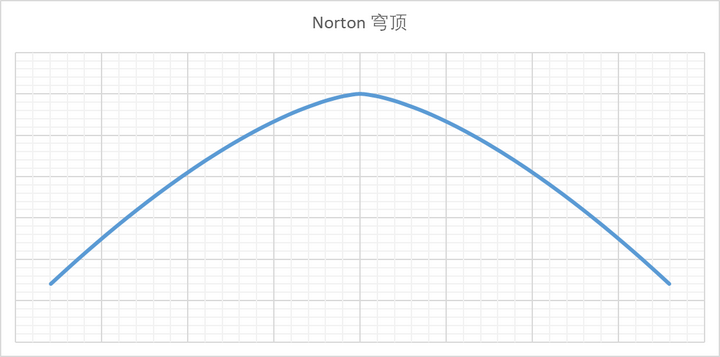
也就是说,一切条件都看起来非常的“物理”。但是仍然出现了一个奇特的解。
对这种情况,我们无非就是如下的几种思路:
1、讨论模型本身的物理性,也就是说,这种曲面是物理上可实现的吗?题中的初始条件是物理上可实现的吗?
2、讨论物理含义,也就是说,运动状态,按照我们常规的想法,是由位置和动量确定的。那么高阶导数在其中到底有何意义?
3、讨论经典力学框架的完备性:是否存在着某些边界,导致经典力学的失效?例如说是否需要光滑的边界条件(或者说至少是原则上是光滑的)?
4、认同 Norton 的说法,经典力学根本就不是我们以前认为的 —— 完全决定论的。
另外,再次强调,这个悖论之所以那么有趣,是因为它在完全无外力扰动的条件下发生的。那些讨论扰动的,统统也都跑题了。即使是在后面计算出来的加加加速度的突发阶跃,也不是什么扰动造成的,而是它本身就是孤立系统满足微分方程的一个解。也就是说,这种突发是一种完全不违背物理定律的、无外力引发的突变。
至于评论中有人认为,动力学方程隐含了一个前提,就是“质点动起来了”,然后外推到静止情况导致悖论的出现。我很疑惑不解,这个评论为何会有人点赞。一切动力学方程,都不存在这种前提。静止解(数学上称为不动点)如果不能被动力学方程容纳,整个动力学早就完蛋了。
但是评论区中有一个评论引起了我的注意,来自一个和著名瑞士生物学家重名的网友, @Wilson·Edwards:

仔细看了一下,还真的是这样的,在顶点处曲率确实是发散的。在物理上这意味着什么?这意味着所有经过此的质点其加速度都是发散的,只除了完全静止一种情况之外。
因为,任何一个曲线运动,其向心加速度都是:
曲率发散就意味着加速度无定义。
那么,唯一一种保持加速度良定义的情况就是,它一直保持静止不动。其它任何一种运动状态都会导致加速度发散。
加速度发散是什么意思?这意味着,它已经无法呆在曲面上了:它会脱离曲面“飞起来”。也就是说,任何在顶点处非静止的情况,小球都会脱离曲面。
然而,我们的运动方程,是按照小球一直呆在曲面上来列的。
也就是说,要么,小球一直静止,且符合我们模型的前提,要么,它“自发运动”,但是却和我们的模型不符了。然而,这种“自发运动”却是这种不相符的模型预言的,因此这种预言也就没有效果了。
这可能是一个最有说服力的矛盾了。
在此,再一次感谢瑞士生物学家给我的灵感。
更新 2022-8-10,第二次更新:
果然还是不行啊,要是这么容易解决的话,怕是不能成为一个广为讨论的悖论了。谢谢评论区中的两位 @东方既白, @李明:


相空间连接轨迹唯一,和此处加速度实际上不发散,应该是同一件事。
关于 @东方既白 的分析,这里不复述了,传送门如下:
似乎我应该试着把这个体系的相图画出来,可能会有所帮助?先记下来,回头再来更新。
或者说可以加一个微扰参数,然后对这个奇异点做一个分岔分析,可能会有用……
但是似乎问题的方向变成了这样一个问题:在特殊边界条件 / 初始条件下(如不满足 Lipschitz 连续性条件),高阶导数或者全局约定是否是限定系统演化的必要条件?从数学上看,是的,但是物理上呢?
更新 2022-8-11:
把这个系统的相图画出来了:
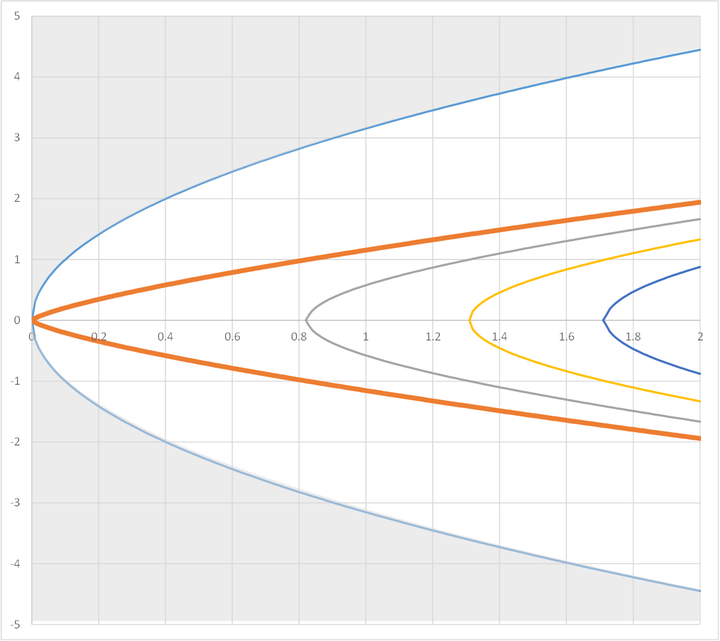
这个图中,灰色覆盖的区域为小球“起飞”的区域,也就是说它因为速度太快而导致无法固定在曲面上。这个区域中,上述的动力学方程不再满足。图中橙色的加粗曲线就对应着小球在顶点时速度恰好为零的情形。其余的曲线代表着更低的能量 —— 也就是说,如果我们从底下向上滚动小球,它的动能不足以让它们爬上顶点。而橙色加粗曲线则代表着 —— 如果我们把过程反演 —— 它刚好能够达到顶点的情形。
这个相图验证了 @东方既白 的分析,的确,虽然顶点处曲率发散,但是由于速度的收敛速度大于曲率的发散速度,所以,仍然保证了此时小球的加速度有限。
从相图上可以看到,如果我们用初始微扰的方式,那么 Norton 悖论中的非平凡解的确就对应着微扰趋向于零的极限。(如果我们认为那个诡异的参数 T 就是微扰发生的时刻)。
评论区有不少人提到反演的情形。这的确是一个思路。因为如果我们考虑一个小球从底部以某一个初速度向上爬升的情况,我们有可能避开顶点,而去考虑它的极限情况。这样一来我们就有了解的唯一性保障了。
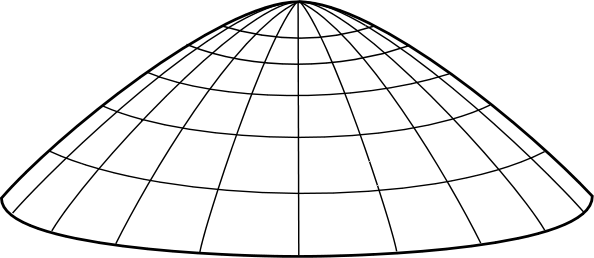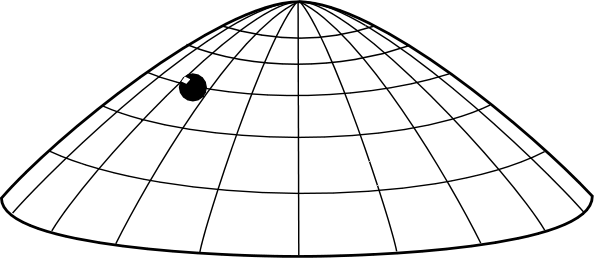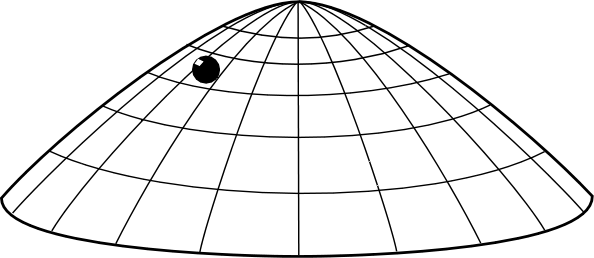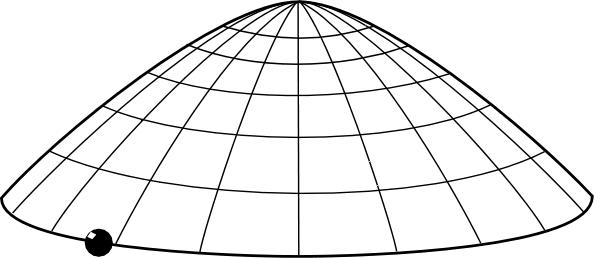
但是这里就发生了一个更加诡异的情况:小球会以有限的时间内抵达顶点且恰好停在那里。
这有何诡异呢?根据时间反演对称性,也就是说,小球不可能稳定地停留在顶点处。这对于一个光滑曲面来说并不是问题,因为根据Hartman & Grobmann 定理,光滑的情况下局部是可以用指数解逼近的。也就是说,小球从稳定状态到开始下落,会经历无穷长的时间才能完成有限的位移。在极限情况,就和它保持静止相自洽了。
也就是说,在这种情况下,时间反演对称也打破了。
我们不妨考虑一个更极端的情况。如果这是一个尖锐的圆锥面会是什么情况呢?尖锐的圆锥面反倒显得不那么反直觉了,因为它的顶点明显不可导,也就意味着顶点的受力直接受到曲面形状的影响,因而就逼得我们对其进行单独的处理。例如说当它受到微扰滚落的时候:
基于我们常规的关于“支持力”的认知,它会产生一小段力矩不平衡的过渡时期,它从静止到沿锥面滑落的过程中,必然会有一小段时间发生滚动。而这个滚动过程,则可以非常好地用刚体力学描述出来。也就避免了“在有限的时间内滑落”这种不平凡的结果。
而 Norton 构造的曲面,虽然是不平滑的,但是它只是高阶不平滑。again,按照我们常规的关于支持力的理解(沿法线指向被支撑物),整个受力过程并不会受到来自于这种不平滑的任何影响。

所以, @豹海豹以及人之豹 这里说的说不定是有道理的。因为我们对弹力的“粗糙”约定,导致了因为力学原因(而非动力学原因)而忽略了高阶影响,从而产生了悖论。
或许,我们如果有谁能做出足够繁琐的计算的话,我们也有可能从弹性力学出发,考虑杨氏模量的无穷大极限,说不定能够搞定这个悖论。
当然,这只是一种可能。