这个问题问的好，我在高一刚学习基本初等函数的时候，也问过这个问题：“初等函数以外的函数是什么样子？”但是当时老师没有解答，并告诉我，你以后一定会学到的，现在来看，他说的对。

Q1：有哪些典型的非初等函数的例子呢？这些函数有什么实际含义吗？

典型例子就是人们尝试去计算椭圆的弧长：

其中

是椭圆的离心率

这个积分没有初等函数的有限次组合的解，但是计算中带着这么多积分符号很不方便，那怎么办呢，这时候就需要引入特定的名称表示他们：

第二类完全椭圆积分函数

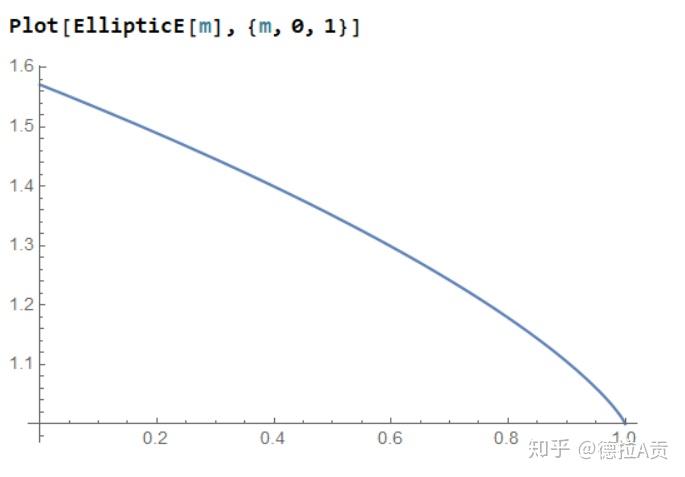
这样椭圆周长

，可以看到，离心率（形状）不变的情况下，正比于半长轴。

想知道大小查表就行了，可以简单验证一下，当离心率

时，就是圆，此时周长=

椭圆周长公式成功收敛到圆的周长公式

。

Q2：那么椭圆积分有什么用呢？

一些其他比较复杂的积分，且无解析解的情况

例如：计算

，是不是看上去很简单，但其实他也是没有解析解的，但可以用椭圆积分表示：

其中 F 是第一类不完全椭圆积分，E 是第二类不完全椭圆积分，

代表其辐角。

当然，建模上 / 工程上如果需要计算这种积分，直接用 Simpson 等格式来数值计算就行了。

Q3：那么除了椭圆积分，还有其他的哪些非初等函数呢？

大学课程概率论和数理统计最常用的两类函数

贝塔 B 函数，又称第一类欧拉积分：

伽马函数，又称第二类欧拉积分

例如高中接触到的正态分布，那一大坨公式，就可以简介的用

来表示。

此外他们之间还有一些有趣的运算规律：

Q4，以上都是定积分相关的非初等函数，有没有其他途径的来源?

还有一大类问题，定义出了很多非初等函数，例如贝塞尔函数，安格尔函数等等

是数学家在解决部分微分方程时，发现他们也没有初等函数解，在后续学习常微分方程，偏微分方程，或者说数学物理方程的课程时，会大量用到哦

例如

的解很容易就知道是

但是形如

并没有一个初等函数的解，那怎么办呢？

第一类贝塞尔函数，就诞生了：

即表示上述常微分方程的解。

纯手打，无复制，如果解决了你的疑惑，希望点个赞支持一下哟~