你去找根绳子,那种绷紧了拨一下可以响的那种,当然如果你有现成的琴弦更好。
你拨一下,听听这个响。
再去找一根一样材质的绳子,切一半,拨一下,听听这个一半绳子的响。
就像这样的比例。
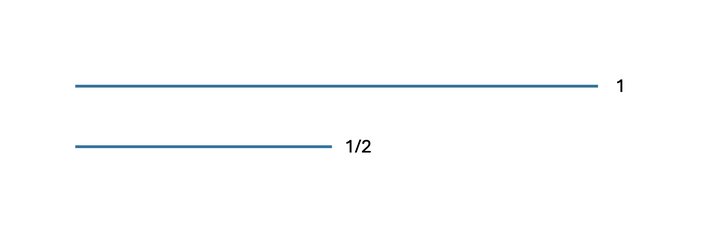
你会发现,这两个音虽然音高不同,但是感觉上是一样的,就像是同一个音。
这个就是一个八度(Octave),或一个音程(Interval)。
这种把弦对半分,得到一个音高更高但听上去一样的做法,在所有文化中普遍存在,也被称为「音乐的基本奇迹(basic miracle of music)」。
有八度现象的存在,想要创造其它的音符,就只需要想办法用不同的方式割绳子就行了。
那怎么割好呢?
割一半这个操作,弦长比例为 1/2,是个最简洁的比例。
那找一个比这个更简洁的比例继续尝试着割不就行了?
第二简单的整数比,是 3/2。
那就用这个数为基准,继续尝试在一个八度内割弦。
比方说,一个八度的弦长是 x,低一个八度的弦长(绳子长和音高是反比)是 2x,那么 3/2 割弦法的第一个音就选在 3/2x 长度这个位置。
第二个音呢,继续乘以 3/2,这时候你得到了 9/4x 这么个数,超过了 2x,也就是超出音域了,这个时候你就除以 2,让它变成 9/8x,就回去了。
如此操作,割六次,你就得到了以下长度的弦。
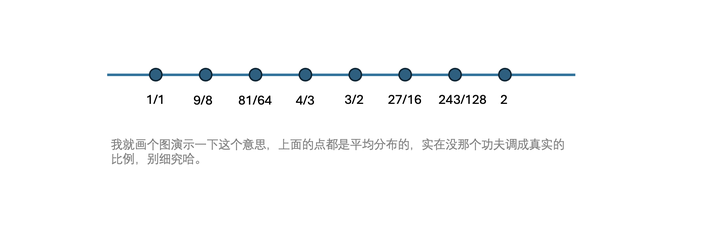
这基本上(重点,是「基本」上,并非「就是」)是现在的大调音阶 CDEFGABC,唱出来就是你熟悉的那七个音,Do Re Mi Fa Sol La Ti Do。
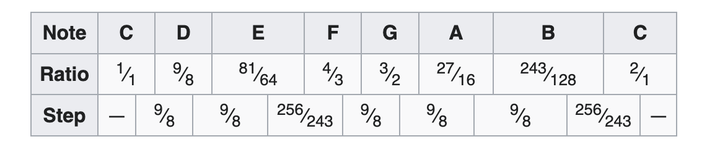
整出这种割弦法的男人,就是那个认为世界上的一切都可以用整数及比例表示,并把发现根号 2 是无理数的学生扔河里淹死的毕达哥拉斯。
这种割弦获取音阶的方法,也是东西所见略同。
在《史记卷二十五·律书第三》中,是如此记载我国的音律的。

九九八十一以為宮。三分去一,五十四以為徵。三分益一,七十二以為商。三分去一,四十八以為羽。三分益一,六十四以為角。
这个意思,就是你把一根弦平均标记为 81 段,取其中的 2/3 段,也就是 54 段长度的,就是徵音,剩下的,宫、商、角、羽,你自己推就能得到。
你按着毕达哥拉斯的方法,多折腾几次,完全可以割出 12 个音,其比例和间隔像是这样:
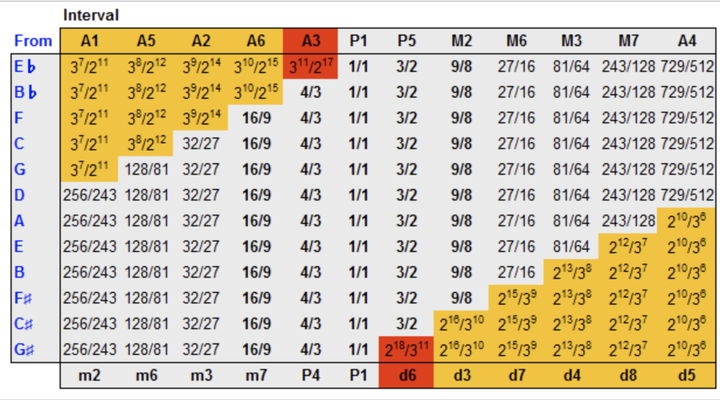
这个图里红色标注的部分,叫做「狼五度(wolf fifth)」,或普罗克拉斯提斯五度(Procrustean fifth),或「不完美五度(imperfect fifth)」。
这个指的是按照毕达哥拉斯的割弦法,就会出现一个五度的,或是跨越七个半音的特别不和谐的音程。
而我们现在所用的 12 音体系却并没有这个现象,这是因为我们现在的 12 音体系,并不是按照毕达哥拉斯这种割弦的方法割出来的。
为了解决毕达哥拉斯方法十二音程中狼五度这个问题,音乐家们各显神通,这个音调高一些,那个音调低一些,凑出了各种各样的平均率(Well Temperament)系统。
不过这些平均率系统只是「听上去感觉平均」,实际上可并不「平均」,虽然他们甚至会把「平均率」这个词儿堂而皇之的写在自己的作品标题里。
对,约翰·塞巴斯蒂安·巴赫,音乐的爸爸,我说的就是你!
而这音律系统怎么整都整不平均,并非欧洲人不想平均,而是他们根本就不会。
要把一段弦按比例割成 12 段,这个操作,用数学语言表示,就是
。
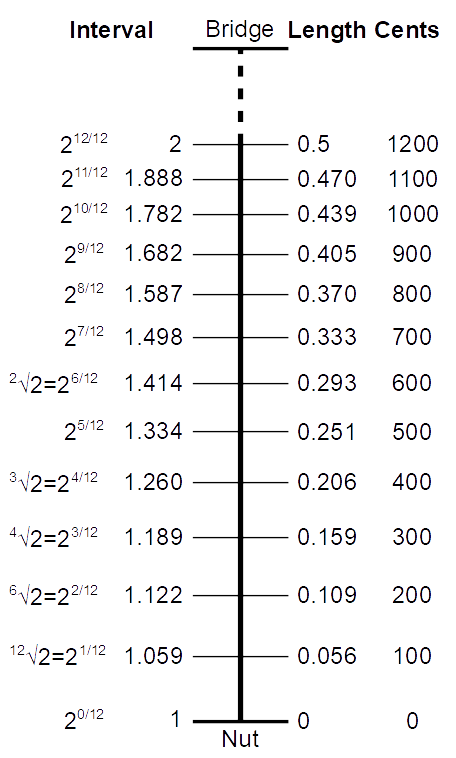
这个数学操作,欧洲人要到 17 世纪才逐渐掌握。
然而在明朝晚期,朱元璋的曾曾曾曾曾曾孙子朱载堉,就已经靠算盘算出了这个数字,并且精确到了小数点后 24 位……

算盘!
计算 2 的 12 次方根!
谁能告诉我,他怎么做到的?我真的想破脑袋都想不出!
这种真正平均的平均率,叫做等率、等程音阶或均分音律(equal temperament),中文翻译也常常直接将其直接翻译成十二平均律,与前文提到的「听着凑合着平均」的十二平均律用相同的译名。
所以,你问哪些数学知识可以用于艺术创作中?
这么说吧,在音乐领域,数学根本就是乐理学的根基。

