因为正态分布通常是由多个相互独立的简单因素相加的结果,而幂律分布则源于多个非独立因素的相互作用。
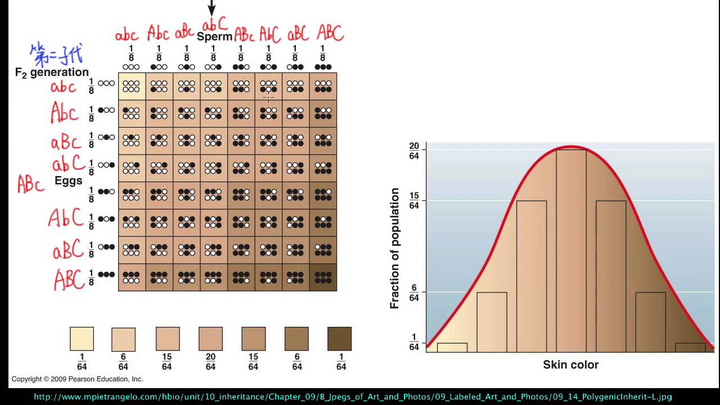
人类肤色分布是典型的正态分布实例。人类肤色由多对等位基因共同决定,每对等位基因的遗传过程相互独立,并且显性基因的数量与肤色深浅呈正相关。
以父母基因型均为 AaBbCc 为例,假设 A、B、C 基因位于不同染色体上。在精子和卵子形成过程中,这三对等位基因的自由组合是随机且相互独立的。在受精过程中,由于精子数量理论上趋于无限,这三对等位基因的组合同样保持随机性和独立性。
因此,显性基因的数量自然遵循正态分布,这也解释了人类肤色呈现正态分布的特征。
我们可以写一个简单的程序复现由简单的相互独立的因素叠加成正态分布的现象.
对一亿
个 01 分布随机变量进行
步加和, 统计加和的结果在
范围内的分布情况.
统计结果如下所示. 可以发现, 我们从统计上证明了多个相互独立的随机变量的加和的结果符合正态分布.
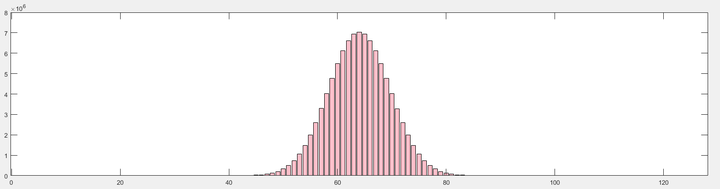
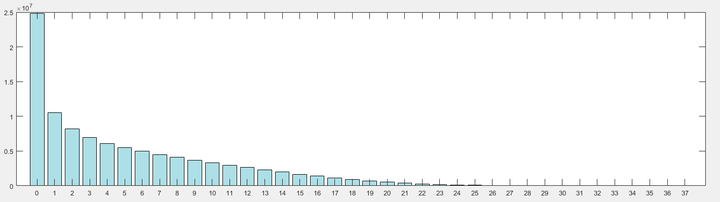
多个相互独立的随机变量的加和的结果符合正态分布, 而多个不独立的随机变量的相互作用的结果则符合幂律分布.
社会财富分布是典型的幂律分布, 幂律分布的表现是强者恒强, 赢家通吃.
如下所示瑞士银行发布的世界财富分布. 按照这个数据, 在中国大陆, 10%的人掌握了 60%的财富.
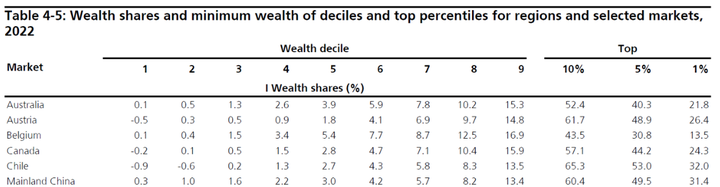
在这么多富人里面, 大部分人的钱都是合法取得的.
这就是资本主义, 朋友, 富人必定会越来越富, 穷人必定会越来越穷, 合理的, 合法的, 自然的. 不是因为所谓的沆瀣一气, 不是所谓的违法所得, 不是所谓的资本打压.
凡有的,还要加给他,叫他有余;凡没有的,连他所有的也要夺去。
《马太福音》第 25 章第 29 节
仅仅是因为资本增值的速度远超劳动的速度, 导致前一次获取财富和后一次获取财富之间有极大的相关性.
而非独立的随机变量的相互作用最终会符合幂律分布.

我们用简单的程序也能验证幂律分布可以源于多个非独立因素的相互作用
我们设计一个模拟人类社会模型, 总共一亿
人, 每人初始金额是一块钱.

在每一步的过程中, 对每个人执行随机的财富流动. 即对每个人, 随机选定一个人与其进行财富流动, 流动的财富数额是其财富的一部分.
PCG32UniformShuffle_Strict
是洗牌算法, 目的是随机选定财富交换的人.
该算法完全公平, 不但富人可以任意比例拿取穷人的财富, 穷人也可以以同样的可能拿取任意比例的富人的财富.

但如此公平的机制, 获得的统计数据却令人惊讶
对个人财富加一取
之后统计各财富分段.
横坐标为
的柱子代表财富在
范围内的人数.
横坐标为
的柱子代表财富在
即
范围内的人数.
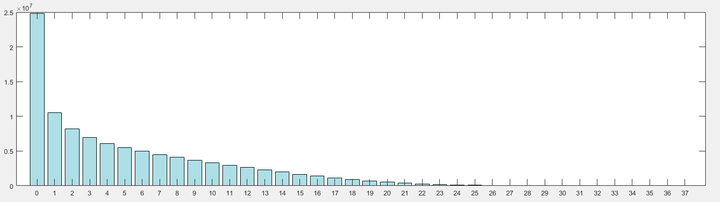
采用
处理是为了数据统计更加明显, 如下所示是未经过处理的源统计数据
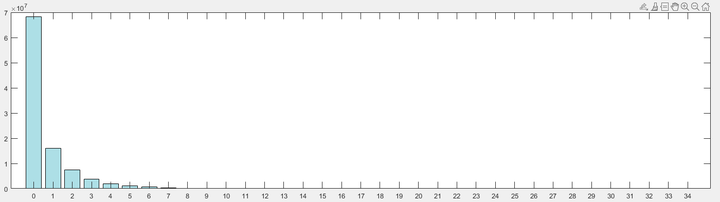
可以看到, 在一个完全公平, 财富自由流动的社会中. 因为财富的积累过程不相互独立(财富只会相互流动, 凭空产生的财富会同时稀释富人和穷人的财富), 自然而然的形成了幂律分布.
实际上, 我们模拟的模型过于简单了, 财富的积累过程中还涉及负债, 复利, 杠杆等复杂模型.
如下图所示是每步利率
情况下的人数 - 财富分布. 未进行
处理. 可以看到, 利率的引入让社会总财富更多了(相当于央行印制货币流入市场), 但穷人还是非常穷, 富人却可以非常富.
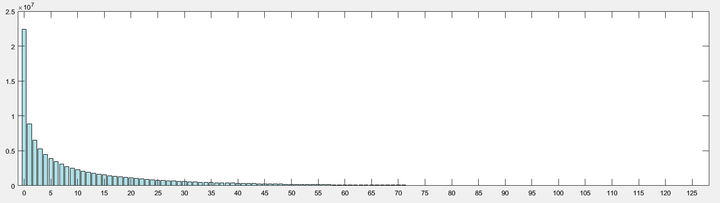
关于本文的数学逻辑问题:
本文提到的服从正态分布和服从幂律分布指的是近似服从正态分布和近似服从幂律分布.
关于人类社会财富符合幂律分布的问题:
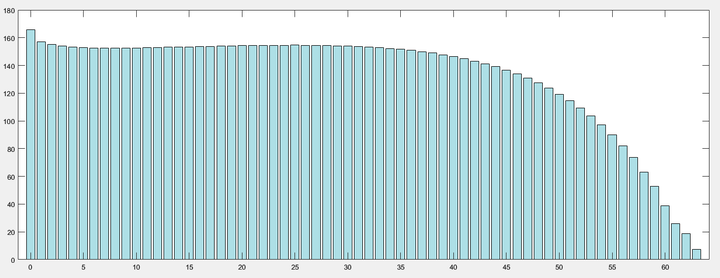
人类社会财富分布符合幂律分布在很多文献中已经有研究, 但本文模拟的财富自由交换模型产生的分布实际上是指数分布. 如下图所示是对人数和财富取
之后的统计情况.
采用的随机引擎:
Pandora Eartha:长期更新, C 语言 head only 高性能随机引擎, 采用 PCG-XSH-RR 算法Pandora Eartha:关于产生离散型均匀分布随机数的一些问题以及正确的办法
#include
#include
#include
#include
#include "PCG32.h"
#include
#include <sys/time.h>
#include
#include
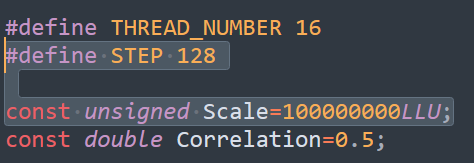
#define THREAD_NUMBER 16
#define STEP 128
const unsigned Scale=100000000LLU;
typedef struct NoramlAndPowerlaw{
unsigned count[STEP];
double accumulate[STEP];
bool normal;
}NoramlAndPowerlaw;
pthread_mutex_t mutex1;
pthread_mutex_t* mutexThreadIndex=&mutex1;
volatile unsigned threadIndex=0;
void* threadSimulate(void* data){
pthread_mutex_lock(mutexThreadIndex);
unsigned myThreadIndex=threadIndex;
threadIndex++;
pthread_mutex_unlock(mutexThreadIndex);
PCG32Struct PCGStatus;
PCG32SetSeed(&PCGStatus,time(NULL)^(pthread_self()^myThreadIndex));
NoramlAndPowerlaw* result=(NoramlAndPowerlaw*)data;
const unsigned myScale=Scale/THREAD_NUMBER;
if(result->normal){
for(unsigned indexScale=0;indexScale<myScale;indexScale=indexScale+1){
unsigned accumulate=0;
for(unsigned indexStep=0;indexStep<STEP;indexStep=indexStep+1){
accumulate=accumulate+(PCG32(&PCGStatus)&1);
}
result->count[accumulate]=result->count[accumulate]+1;
}
}else{
double* wealth=(double*)malloc(sizeof(double)*myScale);
unsigned* exchangeIndexes=(unsigned*)malloc(sizeof(unsigned)*myScale);
for(unsigned indexScale=0;indexScale<myScale;indexScale=indexScale+1){
wealth[indexScale]=1;
exchangeIndexes[indexScale]=indexScale;
}
for(unsigned indexStep=1;indexStep<STEP;indexStep=indexStep+1){
PCG32UniformShuffle_Strict(&PCGStatus,exchangeIndexes,myScale);
for(unsigned indexScale=0;indexScale<myScale;indexScale=indexScale+2){
double amount=PCG32UniformReal(&PCGStatus,0,1)*wealth[exchangeIndexes[indexScale]];
wealth[exchangeIndexes[indexScale ]]=wealth[exchangeIndexes[indexScale ]]-amount;
wealth[exchangeIndexes[indexScale+1]]=wealth[exchangeIndexes[indexScale+1]]+amount;
}
}
for(unsigned indexScale=0;indexScale<myScale;indexScale=indexScale+1){
unsigned floor=(unsigned)(log(1+wealth[indexScale])/log(1.1));
result->count[floor]=result->count[floor]+1;
}
}
return NULL;
}
void formNormal(NoramlAndPowerlaw* theradData){
memset(theradData,0,sizeof(NoramlAndPowerlaw)*THREAD_NUMBER);
threadIndex=0;
pthread_t thread[THREAD_NUMBER];
for(unsigned threadIndex=0;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
theradData[threadIndex].normal=true;
pthread_create(&thread[threadIndex],NULL,threadSimulate,(void*)(theradData+threadIndex));
}
for(unsigned threadIndex=0;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
pthread_join(thread[threadIndex],NULL);
}
printf("Normal distribution\n");
for(unsigned indexStep=1;indexStep<STEP;indexStep=indexStep+1){
for(unsigned threadIndex=1;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
theradData[0].count[indexStep]=theradData[0].count[indexStep]+theradData[threadIndex].count[indexStep];
}
printf("%u\n",theradData[0].count[indexStep]);
}
printf("\n");
}
void formPowerlaw(NoramlAndPowerlaw* theradData){
memset(theradData,0,sizeof(NoramlAndPowerlaw)*THREAD_NUMBER);
threadIndex=0;
pthread_t thread[THREAD_NUMBER];
for(unsigned threadIndex=0;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
theradData[threadIndex].normal=false;
pthread_create(&thread[threadIndex],NULL,threadSimulate,(void*)(theradData+threadIndex));
}
for(unsigned threadIndex=0;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
pthread_join(thread[threadIndex],NULL);
}
printf("Power Law distribution\n");
for(unsigned indexStep=0;indexStep<STEP;indexStep=indexStep+1){
for(unsigned threadIndex=1;threadIndex<THREAD_NUMBER;threadIndex=threadIndex+1){
theradData[0].count[indexStep]=theradData[0].count[indexStep]+theradData[threadIndex].count[indexStep];
}
printf("%u\n",theradData[0].count[indexStep]);
}
printf("\n");
}
int main(int argc, char const *argv[]){
struct timeval start,end;
unsigned milliseconds=0;
gettimeofday(&start,NULL);
pthread_mutex_init(mutexThreadIndex,NULL);
NoramlAndPowerlaw* theradData=(NoramlAndPowerlaw*)malloc(sizeof(NoramlAndPowerlaw)*THREAD_NUMBER);
formNormal(theradData);
formPowerlaw(theradData);
gettimeofday(&end,NULL);
milliseconds=(end.tv_sec-start.tv_sec)*1000+(end.tv_usec-start.tv_usec)/1000.0+0.5;
printf("Calculate Time: %u milliseconds\n",milliseconds);
return 0;
}

