无妖自来,人在花果山,刚下筋斗云。
先说结论:
傅里叶变换是把信号从【时域】变换到【频域】。
拉普拉斯变换是想办法把不满足傅里叶变换条件的【连续信号】从时域变换到频域。
z 变换是想办法把不满足傅里叶变换条件的【离散信号】从时域变换到频域。
然后我们再来分析一下这些变换研究的都是什么,以及联系和用途。
【内容提要】
- 什么是频域?
- 什么是傅里叶变换?
- 什么是拉普拉斯变换?
- 什么是 z 变换?
- z 变换有什么用?
【更正记录】
2020-08-10: 感谢 Aegis Liang
- 更正: 三角函数的一大特点是不同频率的正弦和余弦都是彼此正交的,也就是一个三角函数和其它的三角函数内积为 0.
- 补充:信号的傅里叶变换为复数如何画频谱。
1.什么是频域?
我们认知的世界是三维的,所以我们能看到的物体有 长,宽,和 高。
比如,一个箱子,一些物品。

这些物品我们通过眼睛,手,基本就能够辨别。
当然,现实世界里有些“东西”是我们靠眼睛和手,不能感知的,比如:花香和臭屁。好在人类进化出了鼻子。

通过观察你会发现物体,气体,一般都是由物质构成的。如果想更深入的研究,我们只要分析它们的分子组成,无论再复杂的物品,也逃不出一张化学元素周期表。
通过触觉和嗅觉能够感知的物体,一般都很直观,好理解。
而通过听觉感知的声音,就稍微有些抽象了。声音是通过空气振动传播,也就是让空气分子产生波动。你在听一首音乐的时候,让空气振动的电信号大概是长这样的。虽然听起来很美,但是看起来却很乱。
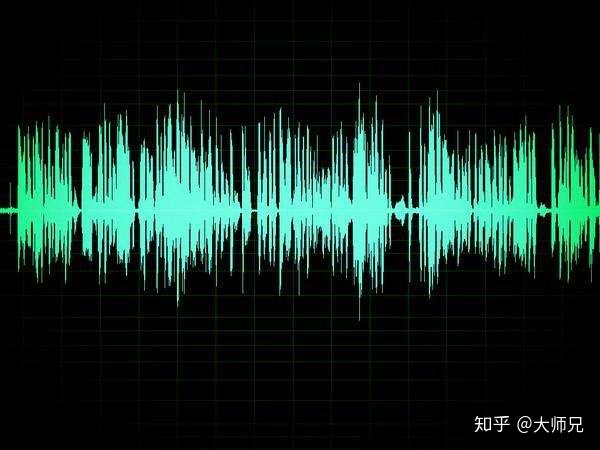
当你对音质有更高的要求,希望低音厚重,中音圆润,高音细腻。怎么对杂乱无章的声音信号进行处理呢? 有没有类似化学元素周期表的法宝,让我们把声音也看得通透。
有!那就是频率,其实这个高、中、低,对应的不是声音大小,而是声音的频率。频率可以理解为信号振动的快慢。
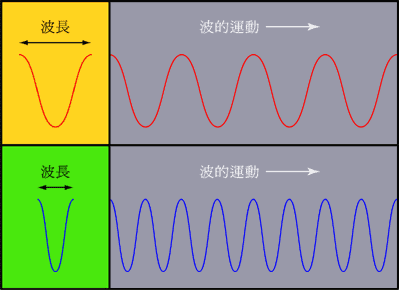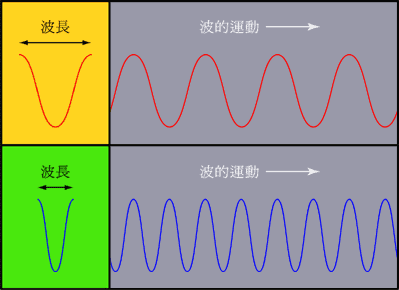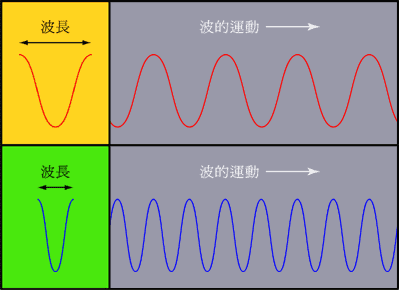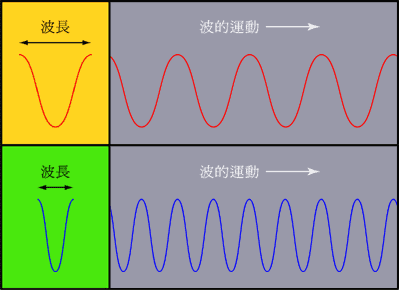
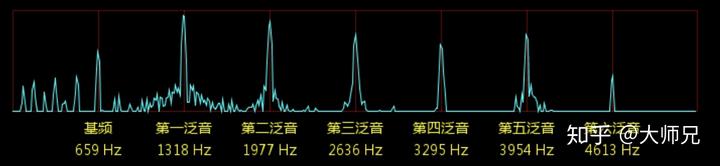
而我们原本看似杂乱的声音信号,可以分解为不同频率的来表示。看起来是不是简洁很多。

如果说声音有些抽象,那么自然界中还有更抽象的:电磁波。
电磁波几乎无处不在,比如我们的手机信号。但它却比声音还要诡异,很难觅其踪影。
人类只进化出了能够感知电磁波中可见光的器官:眼睛。其它的频率,有些人们视而不见,有些像美杜莎一样,看到你就去另一个世界啦。
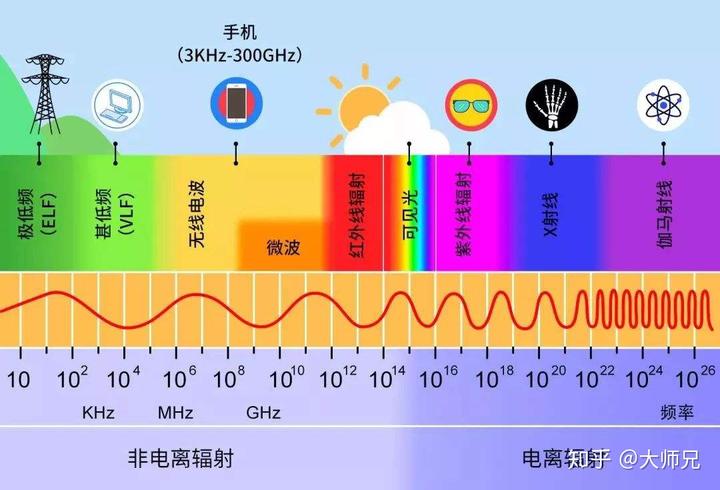
对比一下声音,如果我们想对电磁波做一些手脚,让它们帮我们传递信息,通风报信。如果从时间维度很难操作,它们混在一起,杂乱无章。但电磁波本质是一种波,如果从频率维度去操作就变得相对简单啦。
你仔细品品,电磁波的频率周期表是不是和元素周期表有异曲同工之妙。
那么如何把时域的电信号变到频域呢?
2. 什么是傅里叶变换?
从前有一个特别帅还爱烫头的男人,他叫做傅里叶。

傅里叶早在 1807 年就写成关于热传导的基本论文《热的传播》,向巴黎科学院呈交,但经拉格朗日、拉普拉斯和勒让德审阅后被科学院拒绝,1811 年又提交了经修改的论文,该文获科学院大奖,却未正式发表。傅里叶在论文中推导出著名的热传导方程 ,并在求解该方程时发现解函数可以由三角函数构成的级数形式表示,从而提出任一函数都可以展成三角函数的无穷级数。傅里叶级数(即三角级数)、傅里叶分析等理论均由此创始。
或许是为了更好的烫头,或许是他对大波浪情有独钟,他研究热力学的时候发现任一函数都可以展成三角函数的无穷级数。
怎么理解?比如,有一个方波信号,能不能只用正弦和余弦信号合成呢。
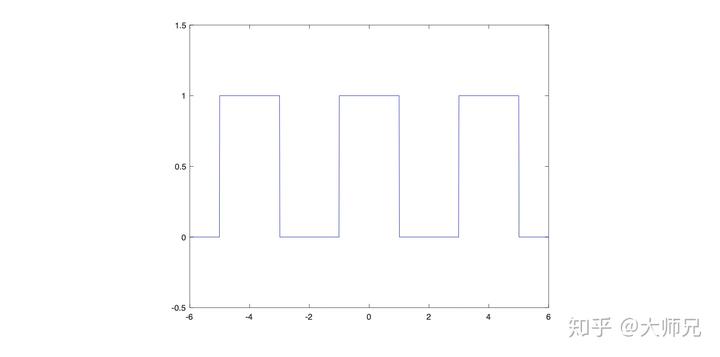
我们试一下:
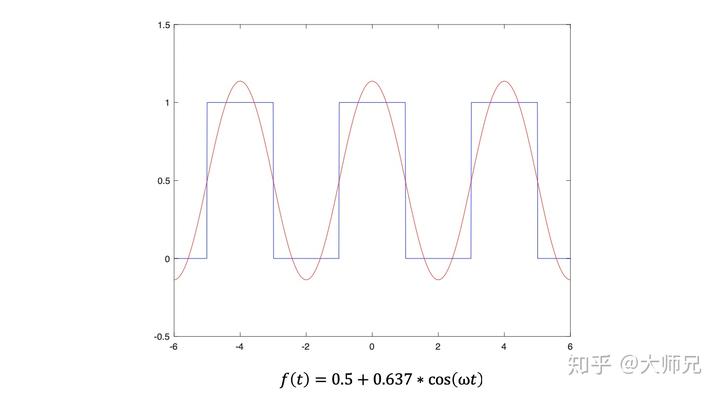
有些轮廓了,我们再来一个:
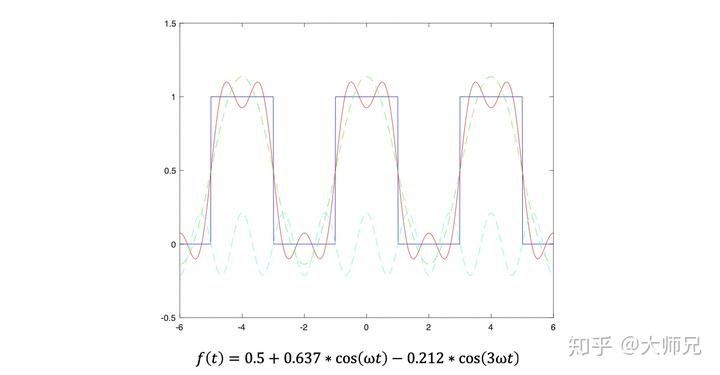
有些接近了,我们再来一个:
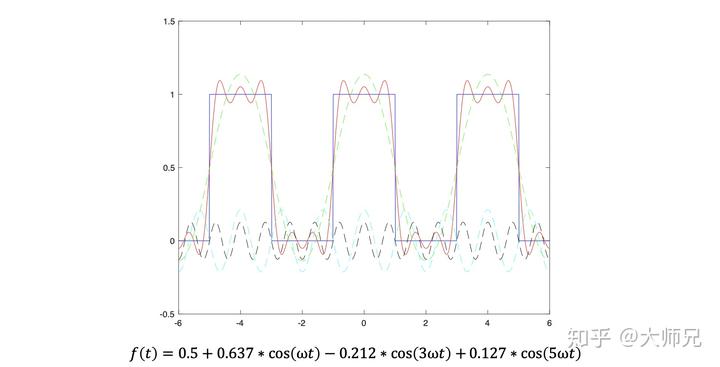
随着我们叠加的余弦信号越来越多,我们得到的信号越来越接近一个方波信号。
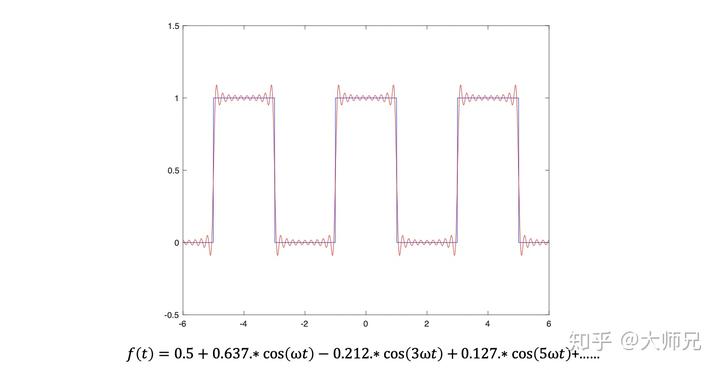
这好比我们用卷曲不一的头发,合成了一个平头。

刚才说的是方波信号。
如果换成其它信号还香不香呢?
香,爱烫头的傅里叶已经证明过了。
为什么这么香呢?
因为三角函数满足一个性质,彼此正交。
什么是正交呢?
举个例子:
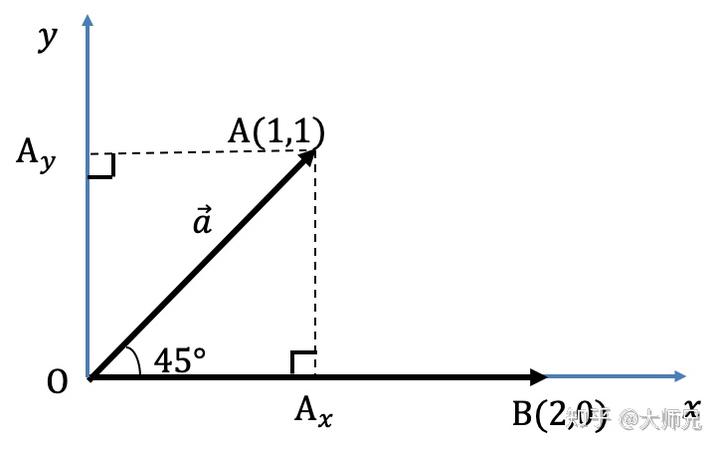
二维空间中,直角坐标系 x 轴、y 轴就是正交的。正交可以理解为它们没有血缘关系,可以结婚生孩子。
二维空间向量 a ⃗ 可以分解到 x 轴、y 轴,对应的坐标为(1,1) 。
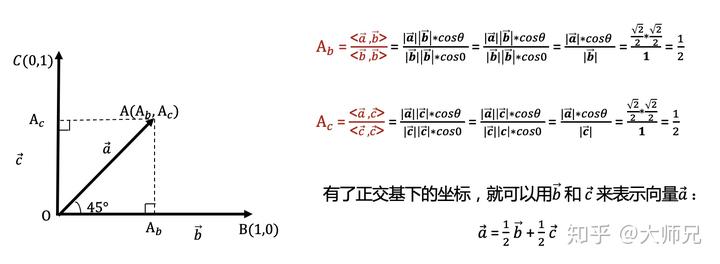
如果在 x 轴、y 轴有两个向量 b ⃗ 和 c ⃗ ,它们是正交的,我们称其为正交基。正交基的厉害之处在于,任意的平面向量都可以用它们去表示。它们是其它向量的再生父母。
比如,想用正交基 b ⃗ 和 c ⃗ 表示向量 a ⃗ ,那么只要求向量 a ⃗ 在正交基下坐标
,
。
同理,如果是三维坐标系,我们只要找到 3 个正交的向量,在不考虑伦理的情况下,它们就可以做为其它信号的再生父母啦。
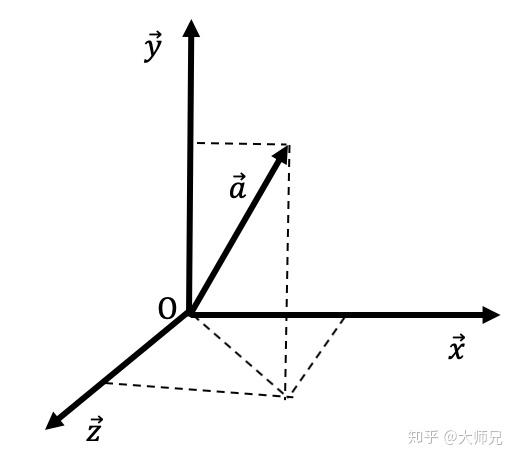
假如是多维空间怎么表示呢,我画个示意图,你要脑补一下,两两向量都是正交的。它们是向量 a ⃗的再生父母们。
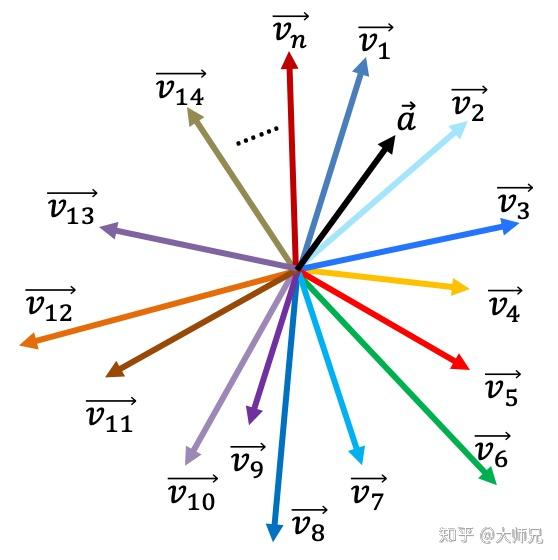
说完了向量,再看另一个种族三角函数。三角函数的一大特点是不同频率的正弦和余弦都是彼此正交的,也就是一个三角函数和其它的三角函数内积为 0。也就是下图中黄色部分的面积和。
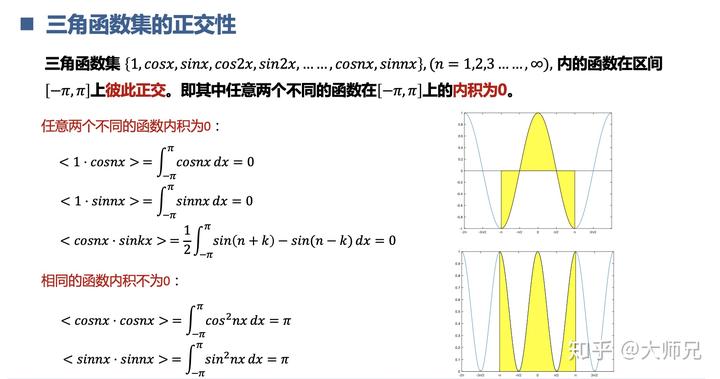
现在开一个脑洞,如果我们把正交的向量换成不同频率的正弦信号和余弦信号会怎么样?
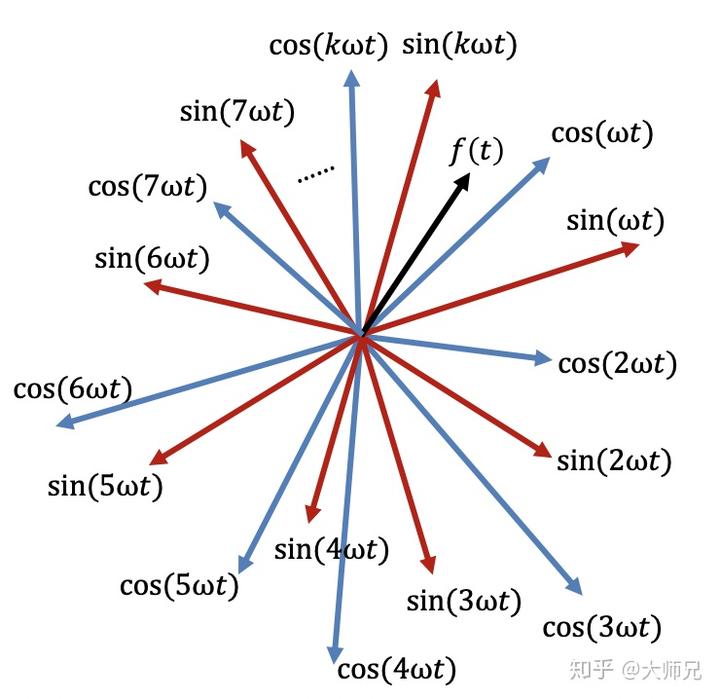
不同频率的正弦信号和余弦信号可以组成任意的信号。比如,方波信号。
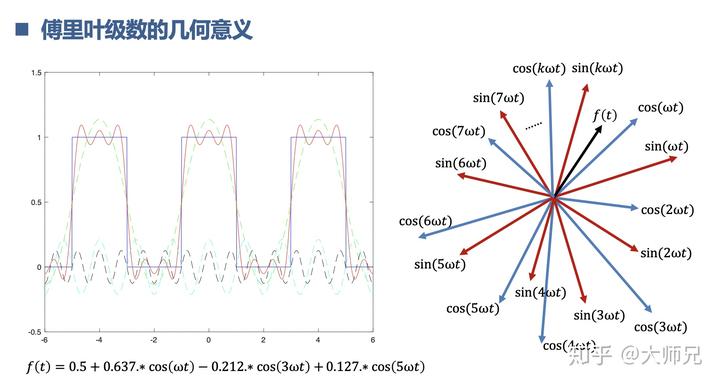
前面对应的系数就是信号
在不同频率的正弦和余弦组成的坐标系下的坐标值。
傅里叶变换就是求坐标的过程。如果忘了,可以复习一下坐标公式。
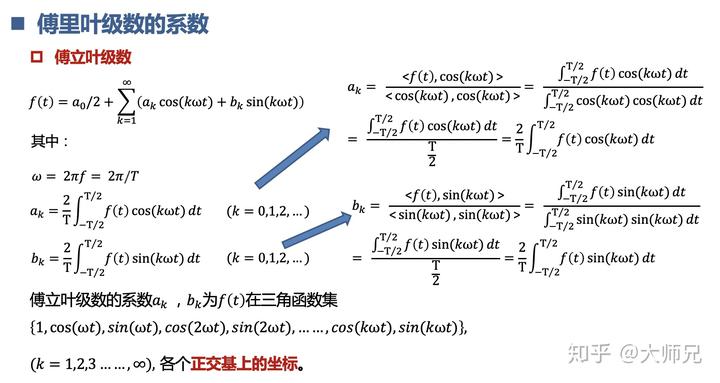
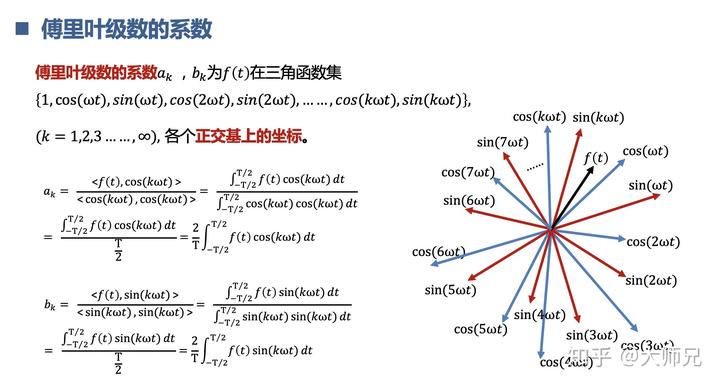
自此,我们可以把大部分信号通过傅里叶变换分解成不同频率的正余弦信号了。比如我们的方波信号,可以用不同频率的余弦信号对应的系数去表示。这样看起来是不是简单很多啦。
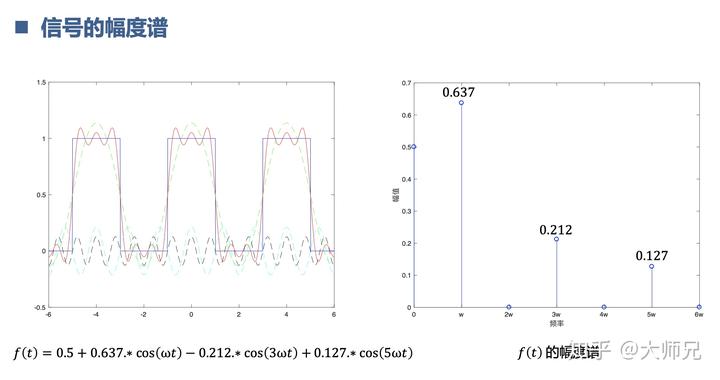
为了让傅里叶变换看起来更简洁,我们根据欧拉公式,引入了复指数形式的傅里叶变换。
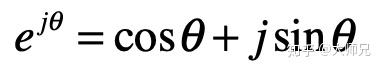
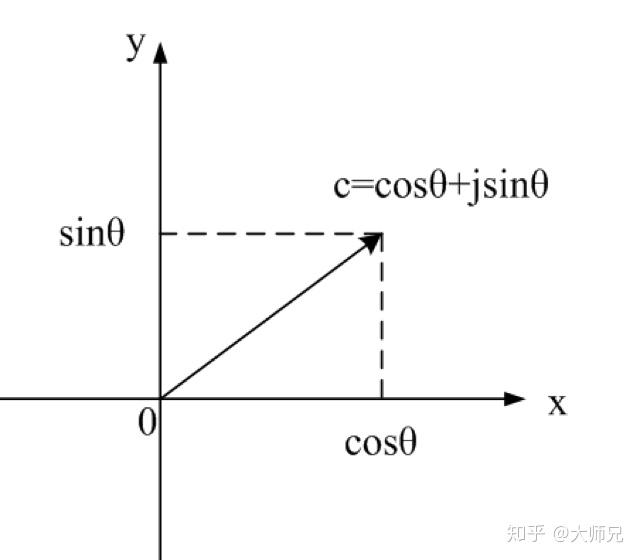
用
去代替
和
。

说来也巧,
也满足彼此正交的性质,也可以作为其它信号的再生父母。
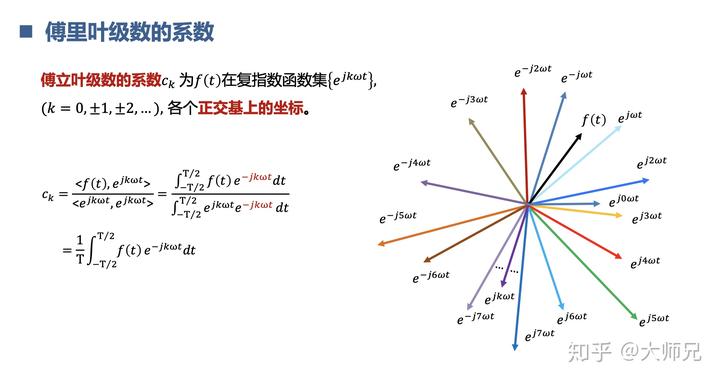
比较一下两种傅里叶级数的展开形式,复指数形式是不是更简洁一些。所以在实际应用中我们也往往用复指数形式去表示。

比如,我们可以把余弦,正弦进行复指数形式的傅里叶变换。其实就是用复指数去表示,并求出在复指数正交系的坐标值。这些坐标值对应的就是不同频率的复指数,也就可以画出信号的频率啦。
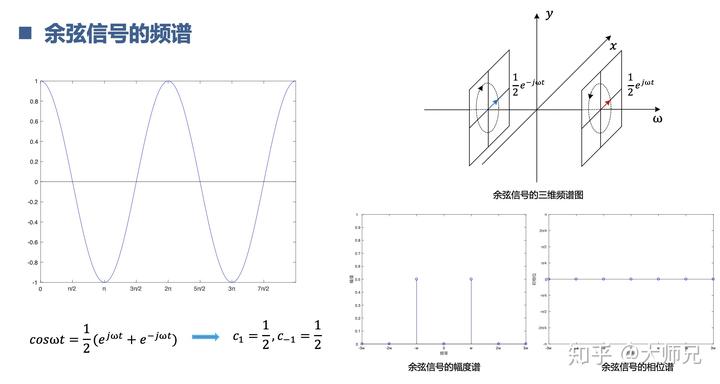
还有些信号傅里叶变换以后系数(坐标值)是复数,比如正弦信号,怎么画出频谱呢?
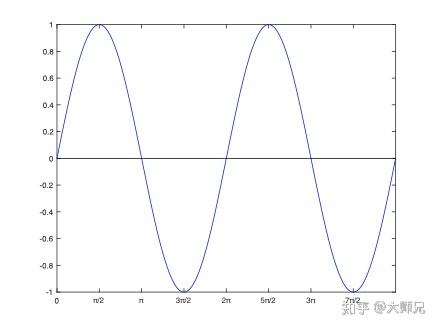
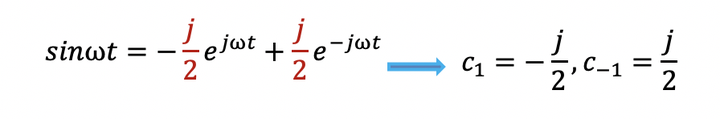
我们知道
就是一个旋转的向量,所以我们可以画一个三维的图像:
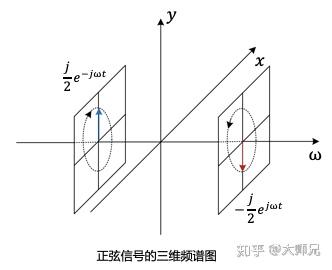
当然这很考验画功,一般情况下我们会把频谱拆解为 幅度谱 和 相位谱。
幅度谱是那个复系数(坐标值)的模值,相位是旋转向量的初相位。
如果不好理解的画,我们可以把公式变换一下,不过先要引入一个虚数的概念。
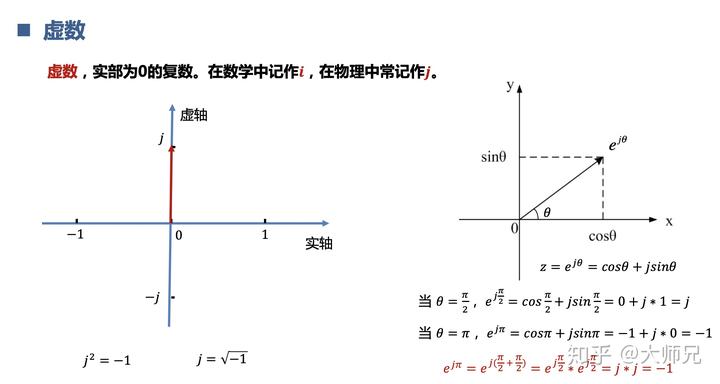
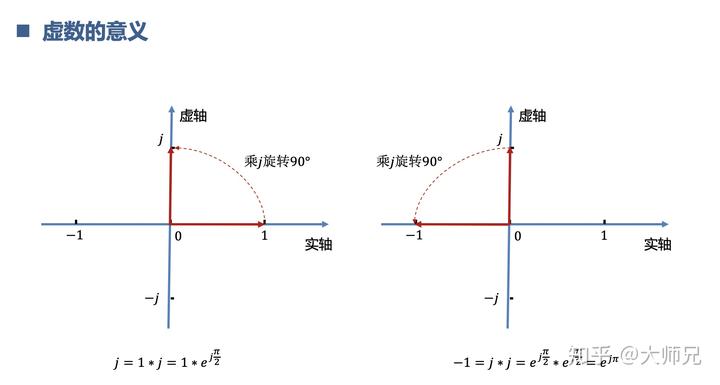
把
带入:
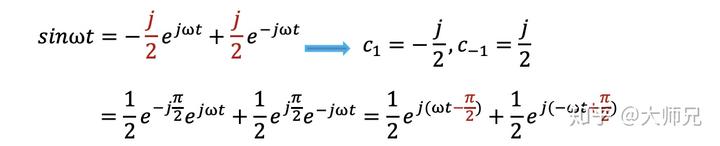
得到
和
是对应的旋转向量
和
的幅值。
和
分别是它们的初相位,也就是
时旋转向量
和
的相位。这样我们可以用幅度谱和相位谱来完整的表示信号的频谱啦。
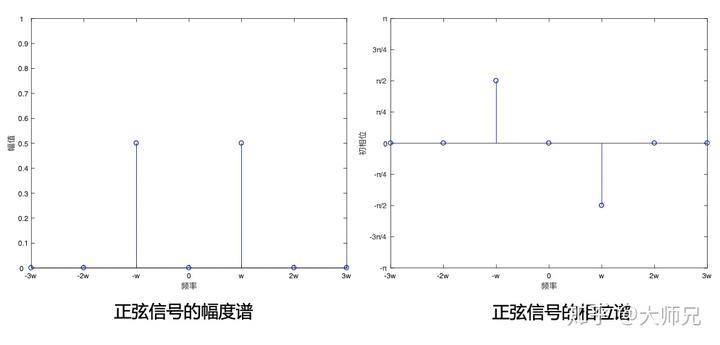
同样,其它信号的频谱也可以用幅度谱和相位谱来表示呦。
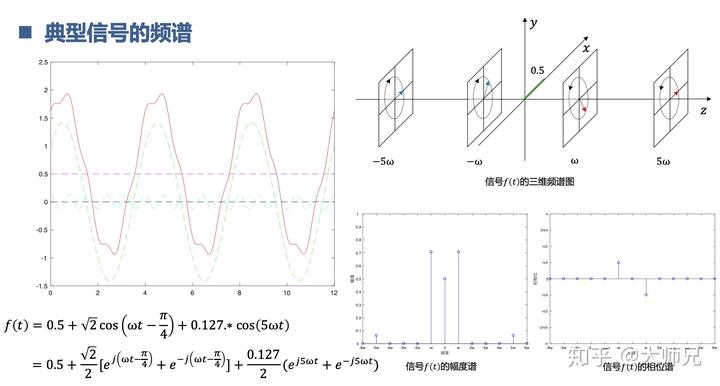
至此,我们知道了一个信号无论多么复杂,我们似乎都能用不同频率的
和
,或者复指数
组合去表示,同时把信号从时域转换到了频域。
所有的信号都能进行傅里叶变换吗?
答案是否。
3. 什么是拉普拉斯变换?
说完了烫头的男人,这里隆重引出另一个男人,一个喜欢养小妖的男人:拉普拉斯。

拉普拉斯提出的一种科学假设。如果有个“恶魔”知道宇宙中每个原子确切的位置和动量,能够使用牛顿定律来展现宇宙事件的整个过程,过去以及未来。

回到我们刚才的问题,不是所有的信号都是那么听话能从时域经过傅里叶变换到频域。
必须是满足狄利赫里条件的信号才能进行傅里叶变换。

举个不满足的例子,比如:
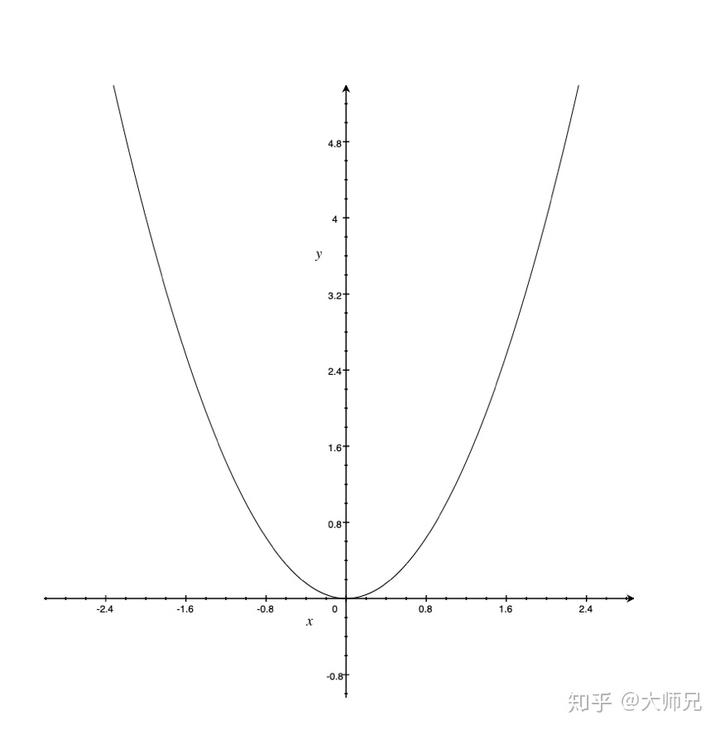
这个函数是无穷大的,我们的复指数信号赶不上它的增长。也就没办法表示它。
不过,我们尝试以其人之道,还治其人之身,给它乘以一个衰减的函数
。
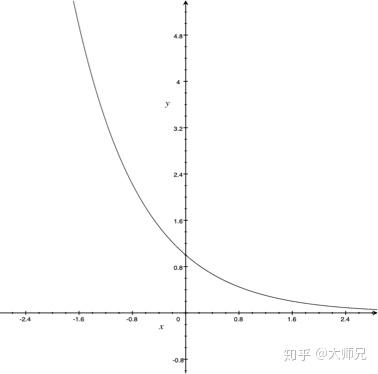
这样原来的直男,被硬生生的掰弯了。。。
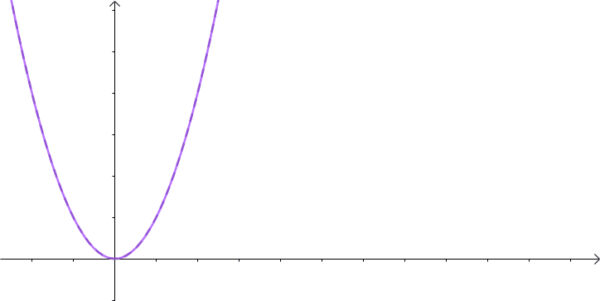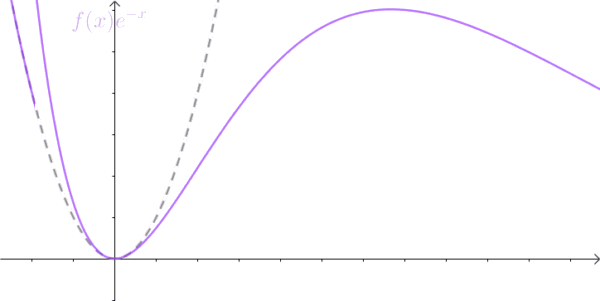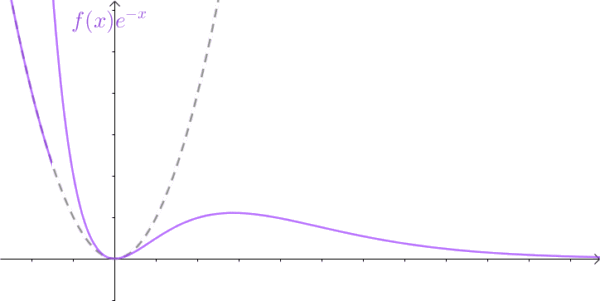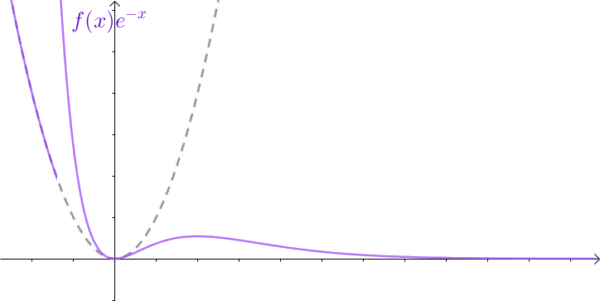
现在不听话的信号乘了一个衰减因子后变的听话了,我们就可以对它动手动脚,进行傅里叶变换啦。不过我们乘的不是
,而是
。

我们令
,得到:

前面我们知道了满足条件的信号,可以通过不同频率的复指数
去表示。
那么这个复指数
是什么样子呢?它是一个旋转的向量,随着时间
,不停的逆时针旋转,旋转的角速度是
。
在横轴的投影值是
, 在纵轴的投影是
。
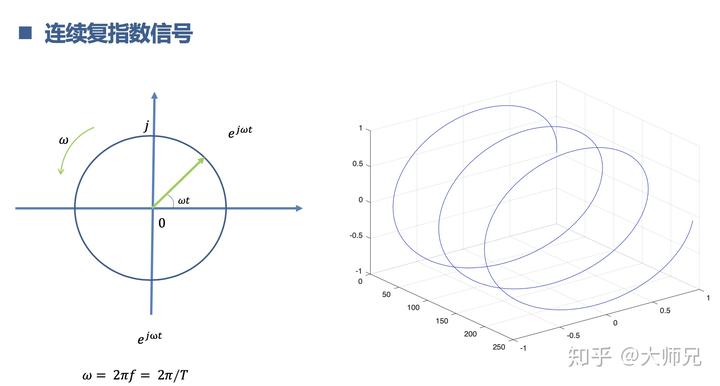
如果我们给复指数
乘以一个放大因子
。则会变成一个不断变大的旋转向量:
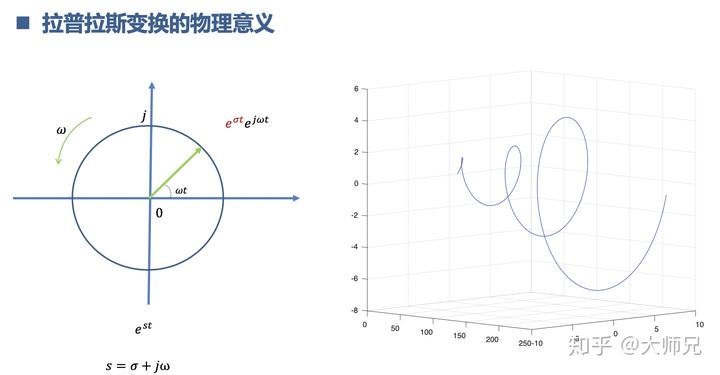
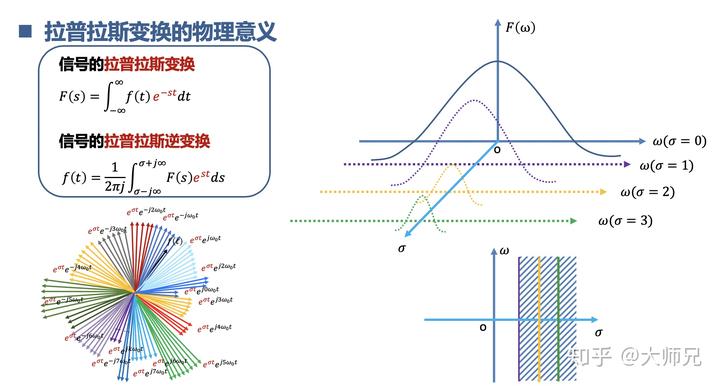
所以可以有 2 种方式来理解拉普拉斯变换:
1.把不能变换的信号乘以一个衰减因子
,先把信号驯服就可以傅里叶变换啦;
2.把复指数信号乘以一个放大因子
,让它追的上要变换的信号。
比较一下傅里叶变换和拉普拉斯。
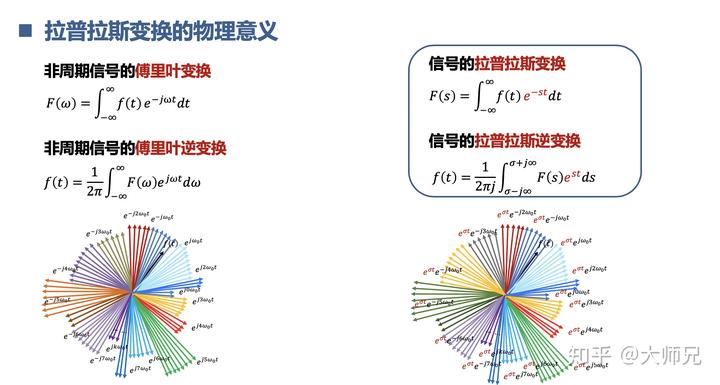
提到拉普拉斯变换的时候,我们还经常提到一个收敛域的概念。其实就是衰减因子
中
取多大值,能让信号收敛后进行傅里叶变换。
时,拉普拉斯变换就是傅里叶变换。
4. 什么是 z 变换?
前面我们讲从时域到频率,说的信号是随时间连续的。
在实际应用中,对于信号的处理都是数字化的。也就是先把连续的模拟信号进行离散的数字信号再进行处理。
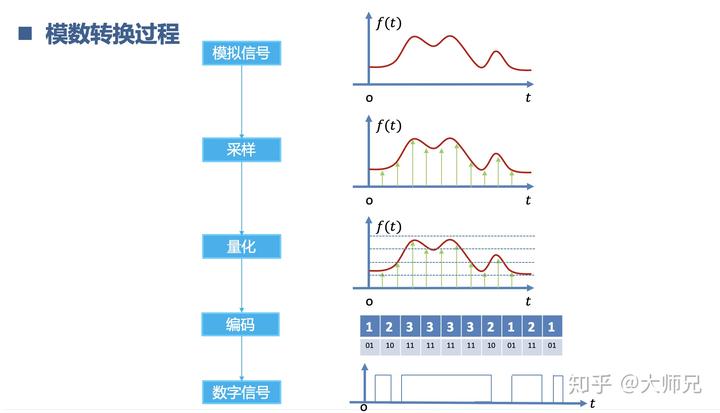
这样我们原来连续的方波信号就变成了,一个个离散的点。
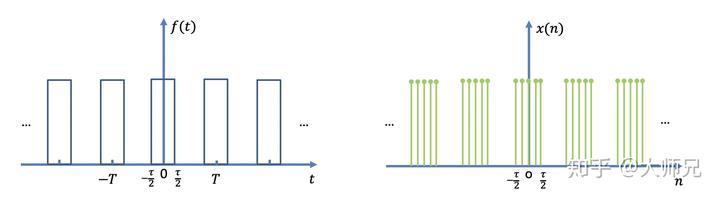
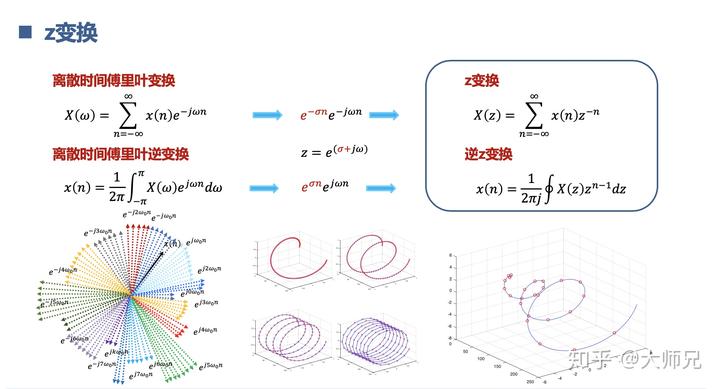
对应的我们也有对于离散信号的傅里叶变换,它们有离散时间傅里叶级数 DFS,离散时间傅里叶变换 DTFT,离散傅里叶变换 DFT,快速傅里叶变换 FFT。
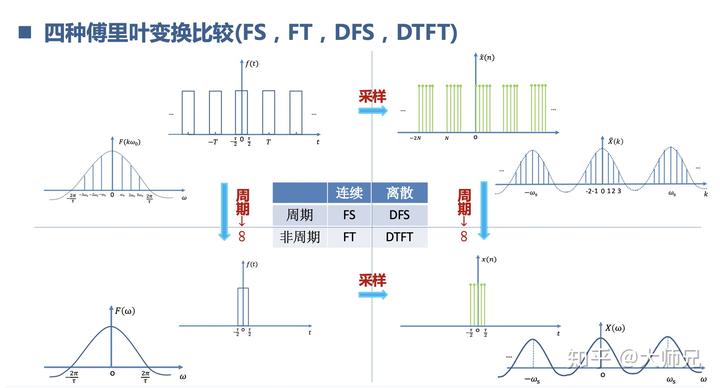
鉴于篇幅原因,我们就不一样展开了,以离散时间傅里叶级数 DFS 为例。
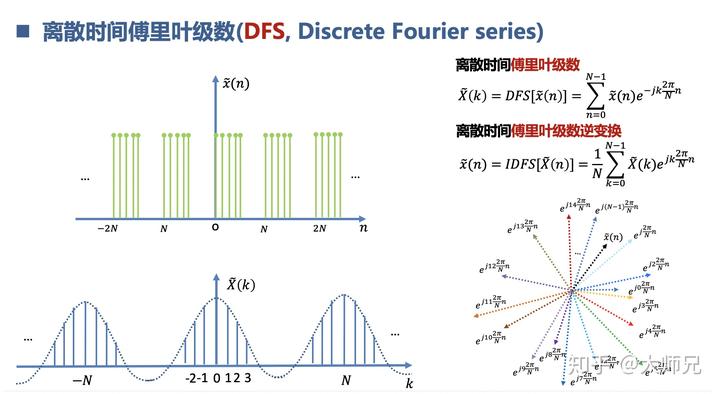
其实就是把数字信号
分解为不同频率的离散复指数信号
,并求出其对应坐标。
离散的复指数信号不再是时间连续的线,而是一个一个点。
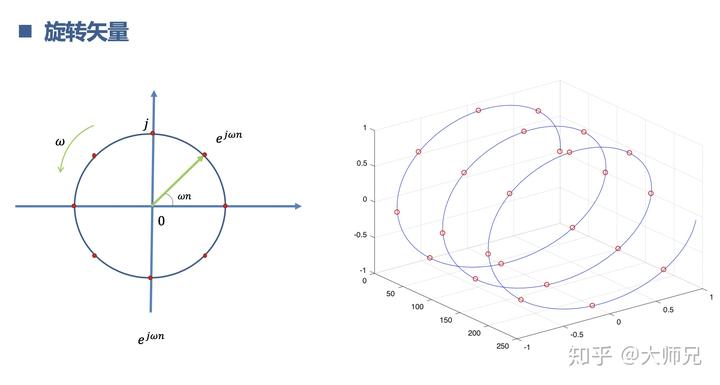
那么所有的数字信号都能够被离散的复指数信号表示吗?
显然不是的。
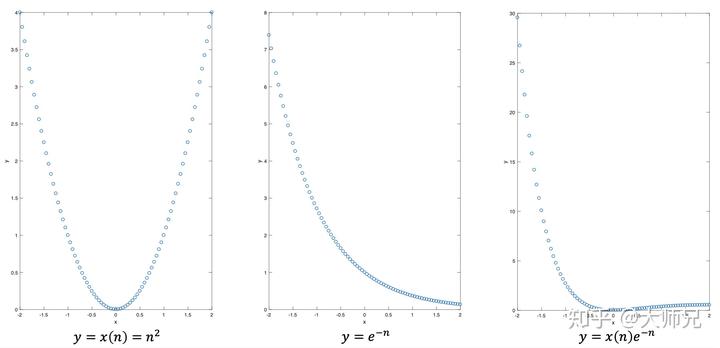
有些信号,本来不听话,变成数字信号后,仍然桀骜不驯。比如:
。不过现在我们有经验了,我们给它乘以一个衰减因子
,先把它掰弯,再进行变换。
另一种理解方法,让离散复指数乘以一个放大因子,不断变大,就能跟上信号的变化,从而降服信号啦。
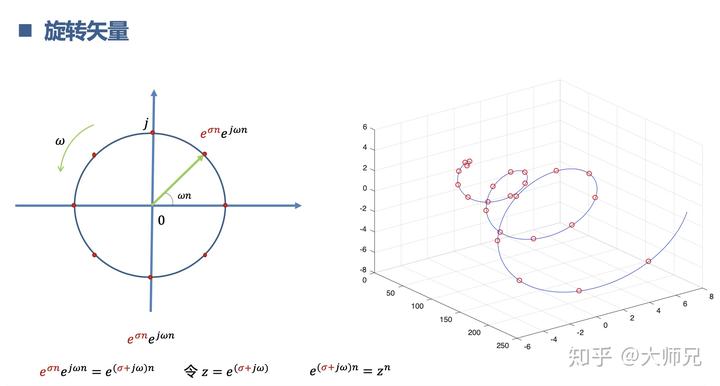
上面说的就是z 变换。其实就是把不能变换的数字信号收敛以后再进行离散傅里叶变换。
是不是和拉普拉斯变换有异曲同工之妙。拉普拉斯变换是对于连续的模拟信号,z 变换对应的是离散的数字信号。
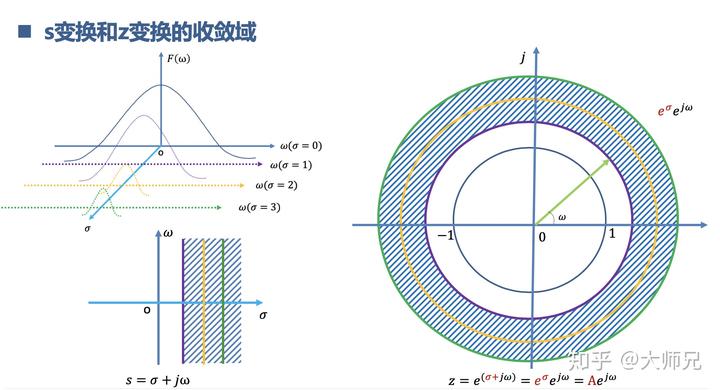
和拉普拉斯变换一样,z 变换也有收敛域的概念。
拉普拉斯
对应的是直角坐标,是一个平面。
z 变换
对应的是极坐标,是一个圆。
5. z 变换有什么用?
费了九牛二虎之力,得出了 z 变换,有什么用?
其实,实际中的信号还是听话的比较多,也就是直接可以进行离散傅里叶变换。那 z 变换是不是没有用武之地啦。

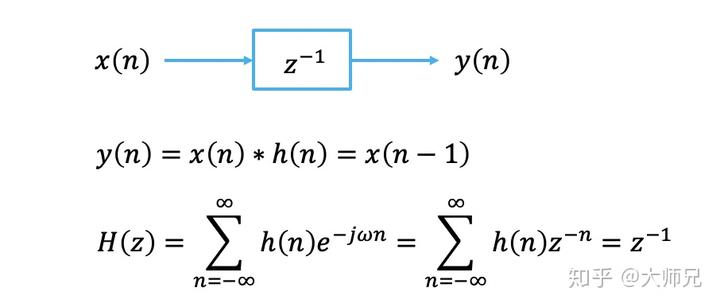
也不是,当信号听话的时候,我们可以让
,那么
. 这样表示起来是不是简单多啦。比如,我们可以简洁的表示一个系统的传递函数。
我们还可以画出系统的频率响应。
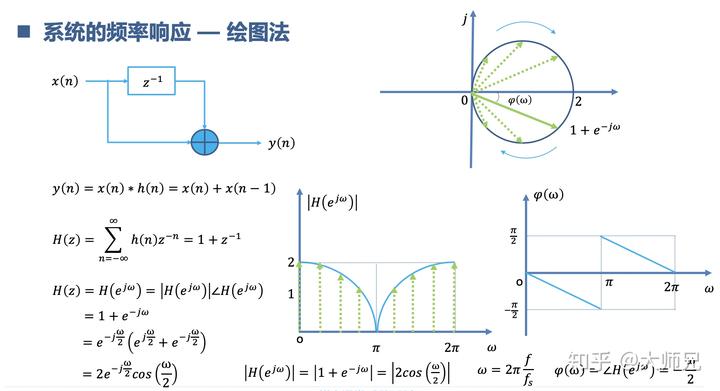
根据系统的频率响应,我们去设计数字滤波器。
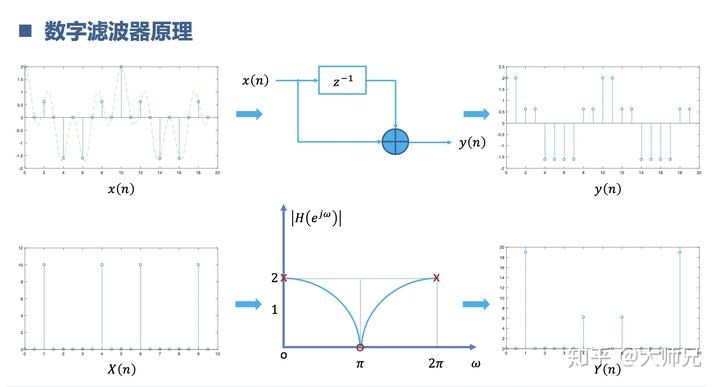
当然,还可以设计更复杂的数字滤波器。

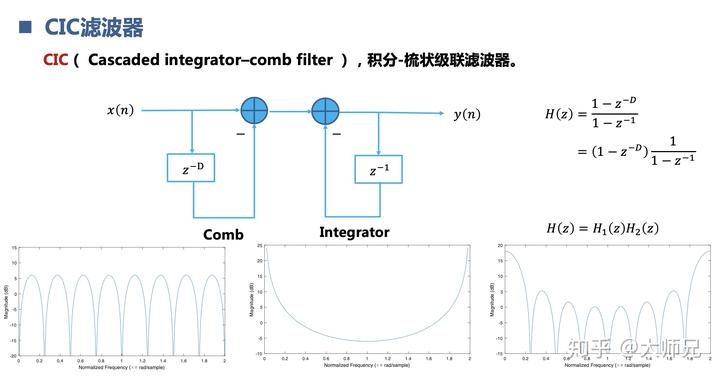
当然,这里的应用仅仅是在数字信号处理和通信工程方面举例。如果有更多的应用,欢迎交流。
对傅里叶变换感兴趣的同学,附上大师兄录制的视频。
深入浅出数字信号处理 - 第 1 讲 - 万法归宗 - 正余弦信号深入浅出数字信号处理 - 第 2 讲 - 傅氏大法 1- 信号与傅里叶深入浅出数字信号处理 - 第 3 讲 - 斗转星移 - 信号与傅里叶

