除了 π，e，0.618，还有没有其他一些有特殊意义的数？ - 趣闻

除了 π，e，0.618，还有没有其他一些有特殊意义的数？

除了 π，e，0.618，还有没有其他一些有特殊意义的数？

知乎精选 2024-06-06 02:00:05

cyb酱，用魔法将数学定理都变成咖啡

〈cyb 酱☆的数学科普系列〉有一个很多人都见过，但是可能叫不出名字的常数：

$\text{Dottie}$

数，或者如果你喜欢，可以叫【计算器常数】

为啥很多人见过呢？相信不少同学都有过这样的尝试，找一个计算器，调整到弧度制

输入任意一个初始值，然后不断按

$\cos$

按键，最后这个数会收敛到：

$c=0.739085133215160641655312\cdots$

当然很多其他的常数也很有趣，我们不求广，宜求少但精，这个数有很多好玩的事情，让我们一一了解他们：

第零，我们先证明全局收敛性

因为不断按

$\cos$

相当于在计算

$\cos x,\cos\cos x,\cdots$

的值

不难发现，因为

$\cos x$

的值域是

$[-1,1]$

，根据偶函数性质：

$\cos\cos x$

的值域是

$[\cos1,1]$

，结合中值定理、压缩映照原理，（其实这个想法挺 Banach 的，不过工具还算是比较初等）

$|\cos x-\cos y|\le(\sin1)|x-y|$

，因此存在唯一的

$x=\cos x$

的解

$c$

而且这个解正是上述迭代的不动点（回顾压缩映照定理证明就是构造

$x_{n+1}=f(x_n)$

现在，我们证明了解的唯一性之后，就可以研究其性质了。

第一，这个数是一个超越数，怎么证明呢？

因为

$2c=2\cos c=e^{ic}+e^{-ic}$

，因此，如果

$c$

是一个代数数

那么不难证明

$e^{ic}$

是代数方程

$x+\frac1x=2c$

的解，从而

$e^{ic}$

是一个代数数

另外显然

$ic$

是代数数的乘积所以也是一个代数数

但是结合我们小学二年级就学过的

$\text{Lindemann}$

定理（就是证明

$\pi$

是超越数的那位的著名定理）

当

$\alpha\neq0$

是一个代数数时

$e^\alpha$

是一个超越数，令

$\alpha=ic$

我们推出矛盾

从而我们证明了

$c$

是一个超越数，这样当然是一个无理数

当然，这个定理显然也能用来证明

$\pi$

是超越数，若不然，

$i\pi$

是代数数

这与

$e^{i\pi}=-1$

是代数数显然是矛盾的，容易发现这与我们上面证明的思路很接近。

第二，现在我们来研究

$c$

的级数表示，利用

$\text{BesselJ}$

函数，我们有

$c=\sum_{n=1}^\infty\frac{2J_n(n)\sin(\pi n/2)}{n}$

，怎么证明呢？（当然如果你愿意，也可以将半整数的正弦写开）

下面的内容来自

$\text{Marc A. Murison}$

在

$1998$

年的文章（但我相信这个级数的发现应该远早于这篇文章），不过总的来说整个证明还是很简单的

首先我们应该联想到小学一年级学过的

$\text{Kepler}$

方程

$\phi=\epsilon\sin\phi+M$

，我们很容易发现：令

$\pi/2-c=\phi$

$c=\cos c\Rightarrow (\pi/2-\phi)=\sin \phi$

也就是上面的方程中

$\epsilon=-1,M=\pi/2$

的情形

所以我们先研究下

$\text{Kepler}$

方程的级数解

很自然的想法是研究

$\epsilon\sin\phi$

看成关于

$M$

的

$\text{Fourier}$

级数

不妨设

$\epsilon\sin\phi=\sum_{k=1}^\infty2b_k\sin(kM)$

于是显然

$\pi b_k=\int_0^\pi\epsilon\sin\phi\sin(kM)\mathrm dM$

对

$\sin(kM)$

分部积分不难得到

$\pi b_k=(-\sin\phi(\pi)\epsilon\cos(k\pi)+\sin\phi(0)\epsilon)/k+I_1$

分部出来的项因为

$M=0$

时解很显然是

$\phi(M)=0$

而

$\phi(\pi)=\pi$

，因此

$\sin\phi(\pi)=0$

于是

$\pi b_k=I_1$

$I_1=\int_0^\pi((\frac{\partial\phi}{\partial M})(\cos\phi)\epsilon\cos(kM))\mathrm dM/k$

注意根据

$\text{Kepler}$

方程

$(\frac{\partial\phi}{\partial M})(\cos\phi)\epsilon\mathrm dM=\mathrm d(\epsilon\sin\phi)=\mathrm d(\phi-M)$

于是

$\pi b_k=\int_0^\pi\cos(kM)\mathrm d\phi/k-\int_0^\pi\cos(kM)\mathrm dM/k$

后者的积分显然是

$0$

，下面考察前者

后者根据

$\text{BesselJ}$

函数的性质，我们变换如下：

首先仍然是利用

$\text{Kepler}$

方程把

$M$

换掉

$\int_0^\pi\cos(kM)\mathrm d\phi/k=\int_0^\pi\cos(k\phi-k\epsilon\sin\phi)\mathrm d\phi/k$

接下来根据

$\text{BesselJ}$

函数的定义

$\pi J_n(x)=\int_0^\pi\cos(n\theta-x\sin\theta)\mathrm d\theta$

（应该可以在特殊函数的书或者是复变、数学物理方法讲柱函数的地方找到）

于是简单观察发现

$\pi b_k=\pi J_k(k\epsilon)/k$

最后，我们就可以写

$\phi=M+2\sum_{n=1}^\infty J_k(k\epsilon)\sin(kM)/M$

回到原题，代入

$M=\pi/2,\epsilon=-1$

同时

$\phi=M-c$

结合我们熟知的恒等式

$1=J_0^2(x)+2\sum_{n\in\mathbb Z^+} J_n^2(x)$

故这个

$\text{Fourier}$

级数是绝对收敛的，于是结论得证

$\blacksquare$

最后，也就是第三，做一点大家喜闻乐见的数值分析

如果使用

$x_{n+1}=\cos x_n$

的方法，收敛速度如何呢？（相当于讨论在计算器不断按余弦的收敛速度）

选取一个合适的初值

$x_0=\frac34$

（误差已经很小了）

很不幸的是速度其实非常慢：

横坐标表示项数

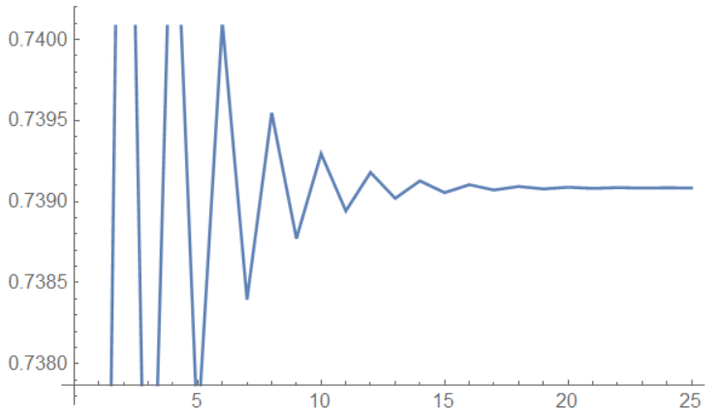
为啥会这样呢？因为这个迭代收敛速度其实是一阶（线性）的

我们不妨设

$e_n=x_n-c$

这样我们有

$e_{n+1}=\cos (e_n+c)-c=\cos (e_n+c)-\cos(c)$

利用微分中值定理我们有

$\cos(e_n+c)-\cos(c)=-e_n\sin\xi_n$

而

$\xi_n$

介于

$c,c+e_n$

之间，考虑到

$e_n$

很小，所以

$\sin\xi_n\approx\sin c\approx0.6736$

因此误差项

$|e_{n+1}|\approx0.6736|e_n|$

，这显然是我们不能满意的

于是我们采用

$\text{Newton}$

法，这显然是一个二阶方法，让我们欣赏一下最后的结果

从图上看，迭代到第五次的时候，已经发现小数点后

$80$

位结果都是真切的

以上。

查看知乎讨论