这个问题有点意思,我来凑热闹讨论一番。
我们知道,当电流通过导线时会产生发热作用,同时导线又对环境散热。导线的发热作用与它的电阻有关,与导线的截面大小和形状当然也有关。导线散热则与它的散热面积有关,与导线的温升(导线表面温度与环境温度之差)也有关。导线发热和散热综合决定了导线的载流量。我们由此隐约感觉到,导线的载流量与导线截面的形状存在一定的关系。
我们寻常所见的导线截面都是圆的,但在工业较大电流条件下使用的部分导线,其截面却是矩形的(包括方形在内),其目的是为了加强散热,等效于矩形截面导体的载流量大于圆形截面导体的载流量。

在我们日常生活中,我们时不时会看到矩形截面的导线或者导电部件,一般都用在较大电流的场合。
题主的问题涉及到平面几何中有关积周比的知识,涉及到导体发热和散热的物理知识。我用中学生能看懂的方式来一番科普吧。
1.从几何积周比谈起,它与题主问题的答案密切相关
我们看下图:
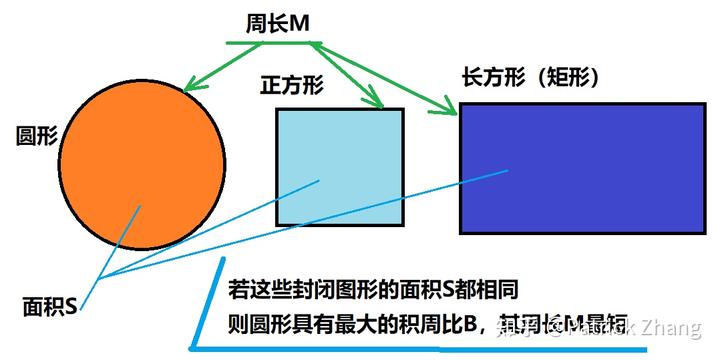
我们以圆形和正方形为例,设它们的面积都是 S,我们来算一算圆形和正方形的周长 M,如下:
我们看到,若 S 相同,则圆形的周长 M 短于正方形的周长 M。
我们把面积 S 与周长 M 之比叫做积周比,用 B 表示。若圆和正方形的面积都是 S,我们来看看它们的积周比 B:
可见,圆的积周比大于正方形的积周比。
事实上,在一切封闭图形中,如果图形的面积相同,则圆具有最大的积周比;如果周长相同,则圆的面积最大。
关于积周比,这可是很有名的一道古希腊几何题。
注意哦,积周比与题主的问题答案密切相关。
2.对导体载流量与题主问题的讨论
我们都知道导体的电阻表达式,如下:
,式 1
这里的 S 是导体截面积,L 是导体的长度,ρ是导体的电阻率,R 当然就是导体电阻了。
我们看下图:
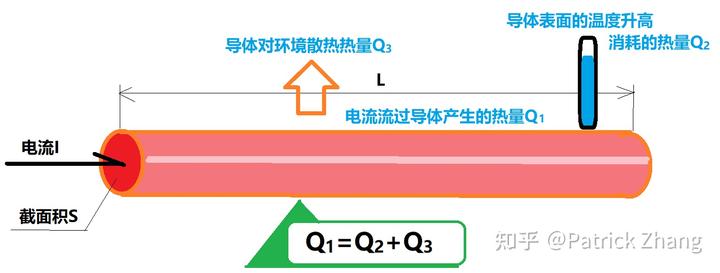
当导体流过电流 I 时,结合式 1,我们可以推得导体产生的热量 Q1 为:
,式 2
式 2 中的 P1 是发热功率,而 t 则是通电时间。
导体自身温度升高所消耗的热量 Q2 为:
,式 3
式 3 中,c 是导体材料的比热容,m 是导体的质量,θ0 是导体之前的温度,θ是导体当前的温度。
导体对外散发的热量 Q3 为:
,式 4
式 4 中的 P3 是散热功率,Kt 是综合散热系数;A 是导体的散热面积,它等于去除掉导体两个端面的表面积,也即导体截面周长 M 与导体长度 L 的乘积;τ是温升,它是导体表面温度与环境温度之差,单位可以用开尔文温标 K,也可以用摄氏度℃;t 是通电时间。
式 4 中的散热功率
就是牛顿散热公式,它是由大名鼎鼎的牛顿推导出来的:

需要说明的是,Kt 综合散热系数是热对流、热传导和热辐射的综合,一般通过实际测量得到。下图是《高低压电器技术手册》中有关 Kt 的表格:
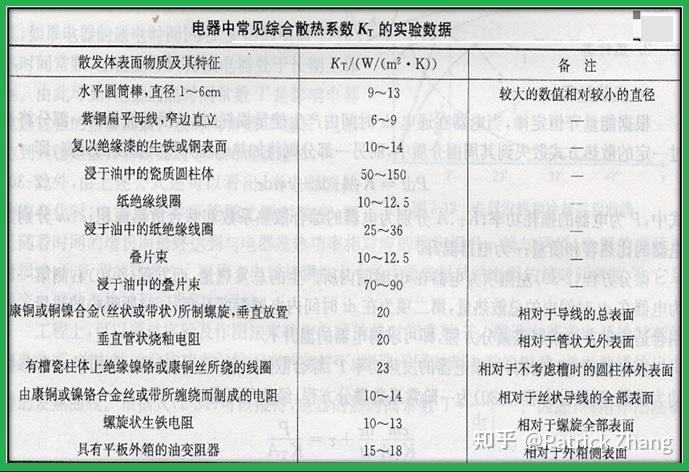
导体通电且当其表面温度稳定后,导体温度不再增加保持一定程度的恒定,于是
,即
。我们由此推出:
。
我们把上式中的长度 L 和时间 t 约掉,再把积周比 B=S/M 代入,得到下式:
,式 5
由式 5,我们得知几件事:
第一:导体的额定载流量与它的最高允许温升
有关,导线的运行温升不得超过
。
第二:导体的载流量与导体的长度 L 无关,与导体的截面积 S 密切相关。
我们由式 5 的电流表达式看到,电流与导体截面积 S 的开平方成正比,与导体的长度无关。这就告诉我们,当我们在查询导线载流量表时无需考虑导线长度的原因,见下图:
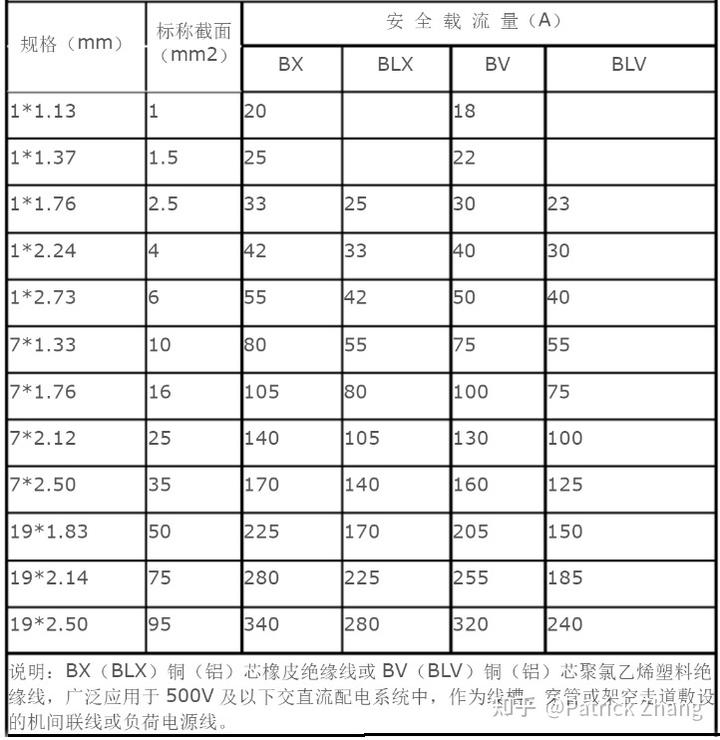
第三:当导体的材料、截面积 S 和流过的电流 I 相同时,圆截面的导体温升高于矩形(正方形)截面导体;当导体的材料、截面积 S 和温升τ相同时,圆截面导体的载流量小于矩形截面导体的载流量。
这第三条就是题主问题的答案了。
第三条的本质原因就是导体截面的积周比。如果圆形与正方形的面积相同,由于圆形的积周比大于正方形的积周比,故正方形的周长 M 大于圆的周长,继而正方形导体的表面散热面积必然大于圆导体的表面散热面积。可见在同等条件下流过相同的电流时,正方形导体的表面温度会更低。这就是正方形导体的载流量大于圆导体载流量的原因。
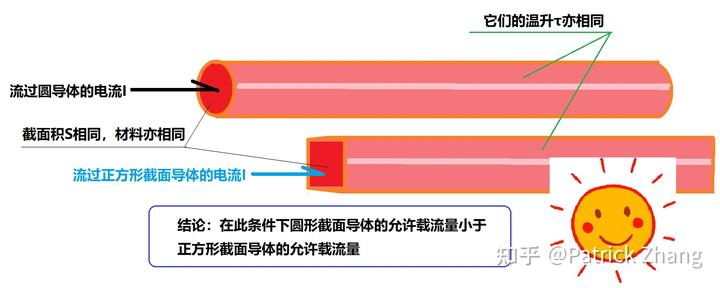
这就是题主问题的答案。有点意思吧?!
3.题主问题的实际运用
在实际电气工程中,例如低压供配电系统的成套开关设备,若电流较大,则主母线一般采取矩形截面的铜排。下图是低压成套开关设备中的母线系统:
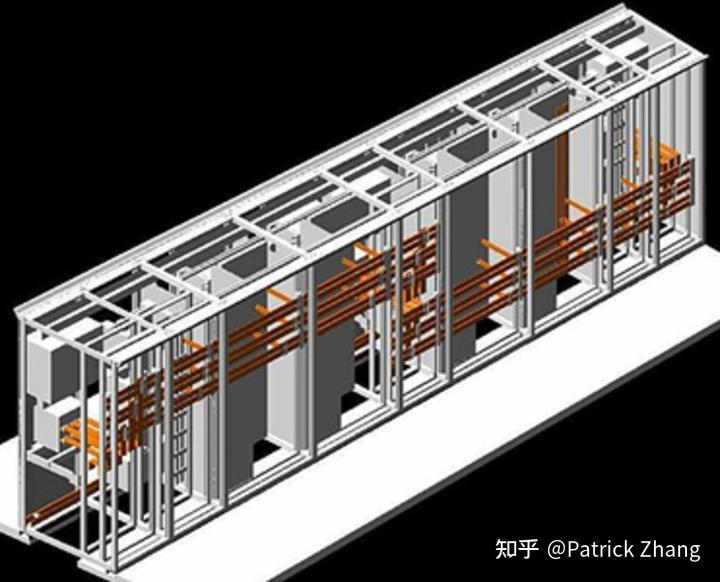
我们看到,图 7 中的大电流导体采用矩形截面的铜排,它的电流最大可达 6300A。

若采用圆导体,不但耗材更多,低压开关柜的散热条件还必须加强,得不偿失。
对于高压开关柜,由于电流较小而电压高,且更加强调电场分布以抑制尖端放电,故母线会采用铜管作为导体。至于小电流的控制线,由于电流小发热也少,当然采用最普通的圆导线为最佳选择。可见,题主的问题必须考虑到运用条件才行。
4.如果考虑到交流电的集肤效应,题主的问题又会如何?
对于交流电,集肤效应和邻近效应是必须考虑的。但对于 50 赫兹的工频来说,集肤效应和邻近效应的影响相对较弱。
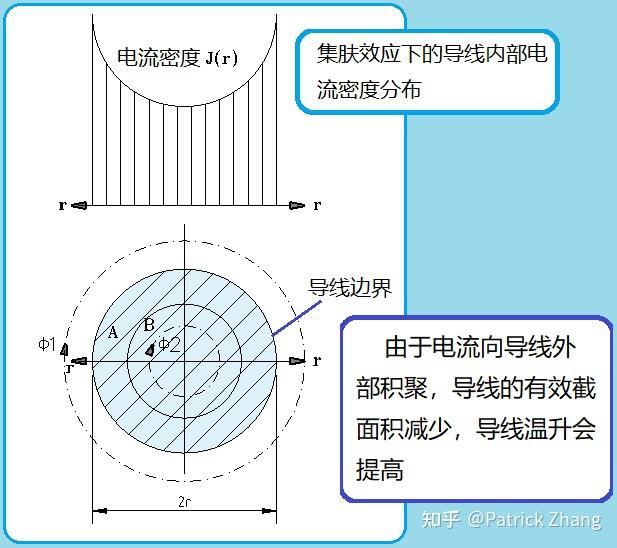
图 9 中我们把导线截面分成外部的 A 和内部的 B 两个区域。请注意:导体内部的 B 区域中相交链的磁通为Φ1 和Φ2,而导体外部的 A 区域相交链的磁通为Φ1。对于交流电的交变磁通,它在导体内部产生了感应反向电动势,阻止原电流的流通。又因为导体中心部位反电动势比外表部分要大,导致导体中心部位电流密度比外表面要小,这就是集肤效应。
系数 Kf 是集肤效应系数 Kj 和邻近效应系数 Kl 的综合。下图是集肤效应损耗系数 Kj 与各参数之间的关系::
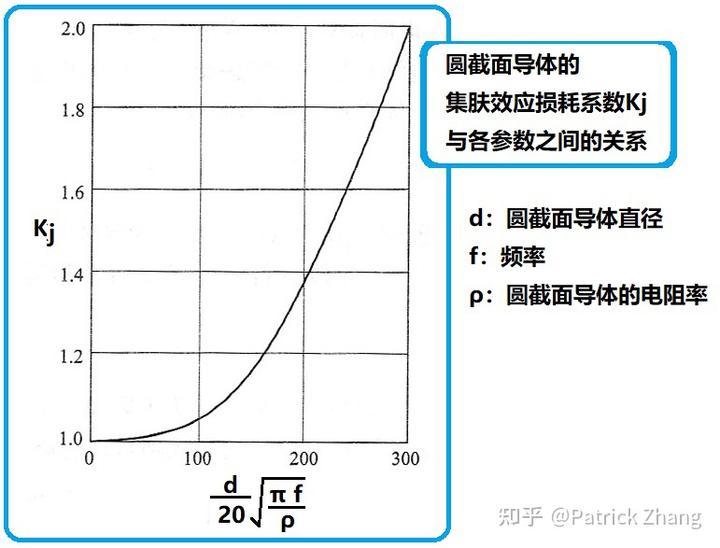
图 10 中横坐标的 d 就是直径。
我们通过一个例子看看如何求得趋肤效应附加系数:我们设直径为 20mm 的铜棒,当通过 50 赫兹交流电时它的工作温度为 80℃,查表求得铜在 80℃时的电阻率为
,于是有:
对照图 10,我们查得集肤效应系数 Kj≈1.02。
我们设导体的直流电阻是
,导体的交流电阻是
,则对于 50 赫兹的交流电, 有:
。我们由此看到,对于 50 赫兹的交流电,集肤效应几乎可以忽略不计。
我们可进一步求得集肤效应产生的穿透深度 b。对于铜导体它的集肤效应穿透深度大约为 9.3 毫米,2 倍就是 18.6 毫米。故铜导体的直径若超过 20 毫米,或者铜排的厚度超过 20 毫米,则其中心部位几乎没有电流流过。
若导体截面是圆形或者正方形,且圆形的直径或者正方形的边长均超过两倍穿透深度,则圆形导体应当改成圆管导体,而正方形导体的内部也应当挖空,见下图:
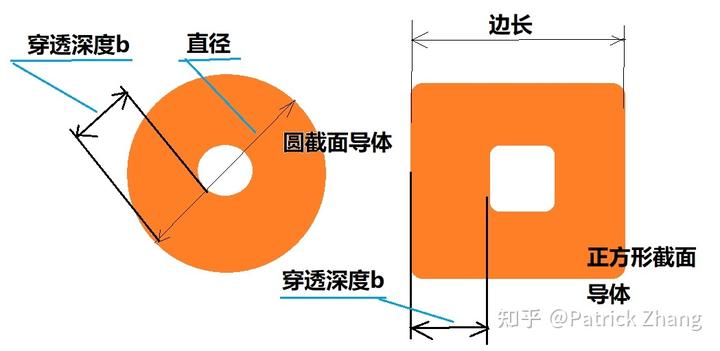
也因此,中压和高压的母线一般采用铜管制作,铜管壁厚一般不会超过 15 毫米。
我们把集肤效应和邻近效应产生的交流电阻附加系数 Kf 代入到式 5 中,得到下式:
,式 6
我们看到,Kf 越大,导体的载流量就越低,导体的温升就越高。可见,频率对导体载流量的影响也不可小觑。好在对于 50 赫兹的工频,Kf=1.02,影响不是很大。
通过本帖的讨论,我们会发现在实际工程中,设计处理大电流导线(母线)是很有讲究的。事实上,母线的设计不但要考虑到截面形状、温升和载流量的关系,还要考虑到日晒、环境温度和机械强度,短路电流下的动稳定性和热稳定性,并且与国家标准、行业规范及国际标准也有很深的关联。
可见,题主的问题背后还是有很多知识的。
补充回答就到这里吧。

