目前的别的回答都是不对的，正解在评论区里，方便起见搬运一下。

首先“展开”这个词需要界定一下，既然直觉上球面不能展开成平面，那为了解释这个直觉，我们要考虑的展开就是指的不拉伸不挤压的变换。澄清一下，匿名用户的答案中提到的变换是需要拉伸挤压的，无论实际生活中还是数学上一般我们都不会把这个称为展开。

先来看球面的情况。稍微一般一点我们考虑三维空间的任意曲面。可以想象如果我在原先的曲面上画一条曲线，“展开”之后的曲面上应当也有对应的曲线，并且长度是一样的。我记得有次小学的寒假作业是求蚂蚁在圆筒上爬行的最短路径，就用到了把圆筒展成平面并且对应的曲线长度不变的这个性质。把这个性质抽象的描述出来，就是“展开”前后对应点的度量张量是不变的。这不是一个很玄乎的概念，直观来看这就是这一点处很短很短的曲线的长度。

然后我们需要用高斯绝妙定理：曲面上每一点处的高斯曲率只与这一点处的度量张量有关。

高斯曲率是高斯在测量大地的过程中定义出来的。在这里简述一下定义。

对于曲面上任意一点，首先选取一个法向量，这在局部来看总是能做到的。然后考虑所有经过这个法向量的平面，这与曲面相交得到一族平面曲线。

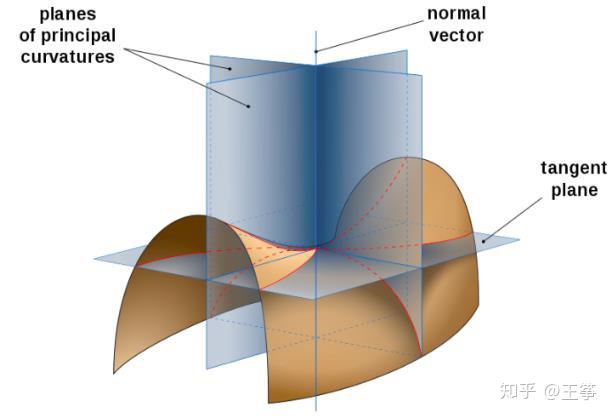
然后对于平面曲线我们有曲率的概念，这是衡量曲线弯曲程度的一个量，这个定义我想一般高数书上可能都有具体的公式，具体来说是：

，其中

是平面曲线的参数表达式。这样定义出来是一个非负的量，但我们这里需要一个正负号。我们刚刚已经选定了一个法向量，所以定义向着法向量方向弯曲的方向为正，远离的方向为负。

然后将平面绕着法向量转一圈，得到一圈曲率，这一圈数会有最大值和最小值，称为主曲率。高斯曲率就定义为最大值和最小值的乘积。

从这个定义中可以看出，高斯绝妙定理真的非常绝妙。因为首先法向量的表达式是不仅仅依赖度量张量的，与曲面如何嵌入三维空间有关。然后曲线的曲率也是不仅仅依赖度量张量的，这一点我们接下来还要用到。但是乘起来就只与度量张量有关了。非常神奇。比如举个例子，之前说的柱面和平面，两者的主曲率是不同的，但是高斯曲率是相同的。

球面上高斯曲率是正数（因为每个截线都是圆，这个曲率可以算出来的），平面的高斯曲率是零（因为每个截线都是直线，曲率是零），所以球面不能展平，结束。

而为什么圆可以展开成直线，是因为一维没有对应的高斯绝妙定理。正如之前所说，曲线也有曲率的概念，但这个曲率不是只与这一点的度量张量有关。本质上，如果只用度量张量去分类，那所有的曲线都是一样的。因为所有的曲线都可以换成弧长参数，这样的话局部上每一条小线段的长度关于这个参数的表达式都是一样的，所以自然度量张量也相同。