问题下很多答主都对平方反比的关系做了探讨,那我就从其它角度聊聊。
实际上,库伦定律和牛顿引力定律的平方反比,都不是严格“正确的”的,因为它们分别是量子电动力学(量子版本的电磁学)和广义相对论在低能低速下的结果,平方反比关系也是近似成立的,而在微观高能以及宇宙尺度上,这两种力的平方反比关系也将不再成立。本回答就看看来自广义相对论和量子电动力学对平方反比关系的修正。
1、广义相对论对牛顿引力的修正
牛顿引力定律中,两个物体受到的引力与二者的质量成正比,与距离的平方成反比,而势能则与距离(一次方)成反比:
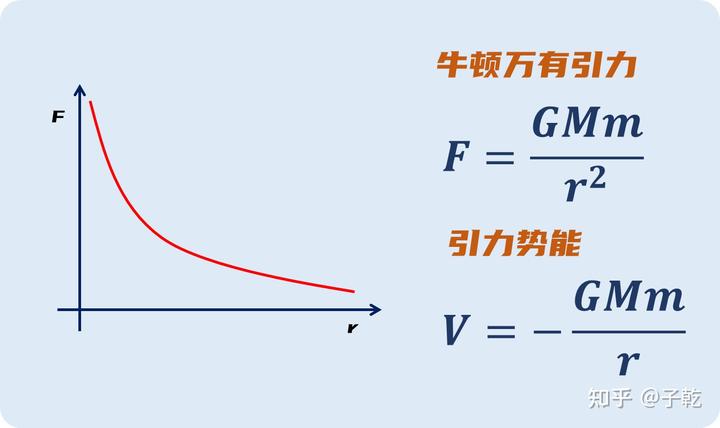
而我们知道,在广义相对论中,物体的运动是要用爱因斯坦场方程描述的,这个方程的左边是时空,右边是能量。著名物理学家约翰·惠勒用一句话概括广义相对论:
物质告诉时空如何弯曲,时空告诉物质如何运动

考虑一个质量为
的中心天体造成的时空弯曲,边上有一个小质量
物体运动,做两个假设:
- 弱场假设,也就是中心天体的质量
不太大,产生的时空弯曲比较小,比如普通的恒星、行星;
- 中心天体的质量远大于小物体的质量,即
。
那么这个小物体受到一个等效的势能为[1][2]:
其中
为约化质量,也可以顺便写出一个等效的力:
其中
是小质量物体的角动量,这里的负号代表了吸引。
可以看到,在广义相对论中,两个物体之间的作用力不再仅仅是平方反比的关系,还多了一个距离四次方反比的项,可以看出:
- 这一项也是吸引力。由于是四次方,因此这一项的效果随着距离的增大而迅速衰减,在距离中心远处的地方跟牛顿万有引力定律就差不多了;
- 这多出来的项是与角动量有关的,也就是说,角动量不同,会改变物体受到的引力大小。而在牛顿万有引力中,引力与角动量没有关系。
2、量子电动力学对库伦定律的修正
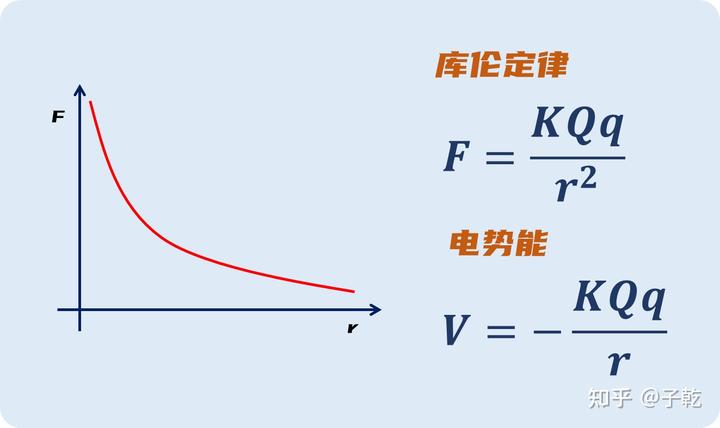
量子电动力学是量子版本的电磁学,一个主要的改变是考虑了量子效应。量子理论中存在一个结论:
真空不空
看似空无一物的真空中,实则是暗流涌动。当然,不严谨地说,就是真空中存在大量的虚粒子对,这些虚粒子对瞬间产生又瞬间湮灭。此处不去纠结这些说法的严谨性,实际上,这些“虚粒子”能产生实实在在的效应。
在量子电动力学中,一个真空中的带电粒子会影响周围的虚粒子:
吸引异性电荷的虚粒子,排斥同性电荷的虚粒子
这就很像等离子体的性质了。而结果就是,我们在一定距离上测到的电荷,并不是“裸电荷”,而是被一堆被极化了的正反电荷包围着,是被稀释了。
具体来说,我们测到的电荷比“裸电荷”更小!
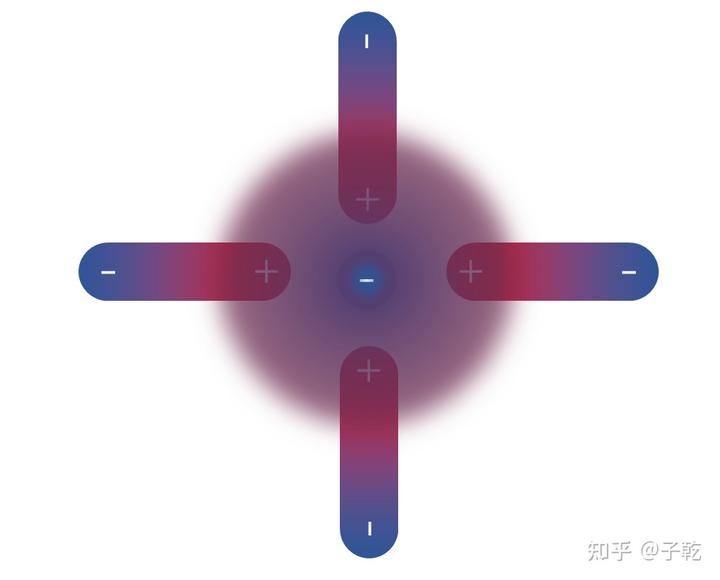
这种稀释作用在不同的距离上也不同,最终导致的结果就是,两个带电粒子的电磁力不再是随着距离成平方反比定律,或者说,电势能不是距离一次方反比。
以正电子和电子(二者相吸)为例,通过量子电动力学的计算可以得到二者的电势能为[3]:
其中
为精细结构常数,
为电子质量。当然,这个结果也是近似,因为只考虑了次领头阶的修正,也就是电荷的四次方,原则上还可以考虑六次方、八次方......的修正,只不过这些修正越来越小而已。
同样地,也可以写出一个力:
很明显,力中多了一个修正项,新的项随着半径的关系比较复杂,但是也能简单地看出:
- 随着距离增大,修正项迅速减小;
- 质量越大,衰减地越迅速,所以这一项只在非常小的距离上有明显作用。
3、强力和弱力
人类已知的四种相互作用中,万有引力以及电磁力在低能下的近似都是平方反比,那另外两种力,即强力和弱力又如何呢?
强力是夸克和胶子之间的,在低能下,则体现为核力,即质子和中子之间的核力。
1935 年,类比在电磁相互作用中,光子为媒介粒子, 日本物理学家汤川秀树认为,强核力也有一个媒介粒子——
介子。

(图片来自[4])
汤川求得了核力势的表达式:
其中
为一个系数,此处不重要,
为
介子的质量。这样一个结果其实很有意思,可以看到,因为势能函数存在一个指数项,因此势能随着距离迅速降低,如果
大,则降低的缓慢,如果
非常小,则势能函数降低的非常迅速。
势能的主要作用范围其实是和
产不多数量级的,此处即
再根据
可以得到:
这就是汤川秀树得到的
介子的质量,后来在 1947 的宇宙线中观测到了这种粒子,其质量为
完全符合预测结果!
另,如果考虑
介子质量为 0 的情况,那么
也就是说传播距离为无穷远,势能函数变为:
这不正好就是静电势嘛!而且光子的质量确实零!
另外,弱力在低能下并没有一个类似的有效力的形式。
4、最后
感觉很有意思,两个宏观低速中的平方反比定律,形式上巧合般地相似。但是二者由都是更大理论的低能低速近似。
有意思。

