一杯 100 度的水可以把一杯 0 度的水最多加热到多少度？63.21 度是极限了吗？

酱紫君，QQ群1014125

确实可以达到 100℃！直接热水放到冷水里最后冷水只有 50℃。

我们可以这样做, 把 100℃ 热水分成两杯红水, 0℃ 冷水都分成两杯蓝水

首先拿起红水 A 和蓝水 A 热交换, 红水 A 50℃ , 蓝水 A 50℃

接着拿起红水 A 和蓝水 B 热交换, 红水 A 25℃ , 蓝水 B 25℃

同理拿起红水 B 和蓝水 A 热交换, 红水 B 75℃ , 蓝水 A 75℃

最后拿起红水 B 和蓝水 B 热交换, 红水 B 50℃ , 蓝水 B 50℃

最后红水 AB 合并变成 37.5℃, 蓝水 AB 合并变成 62.5℃

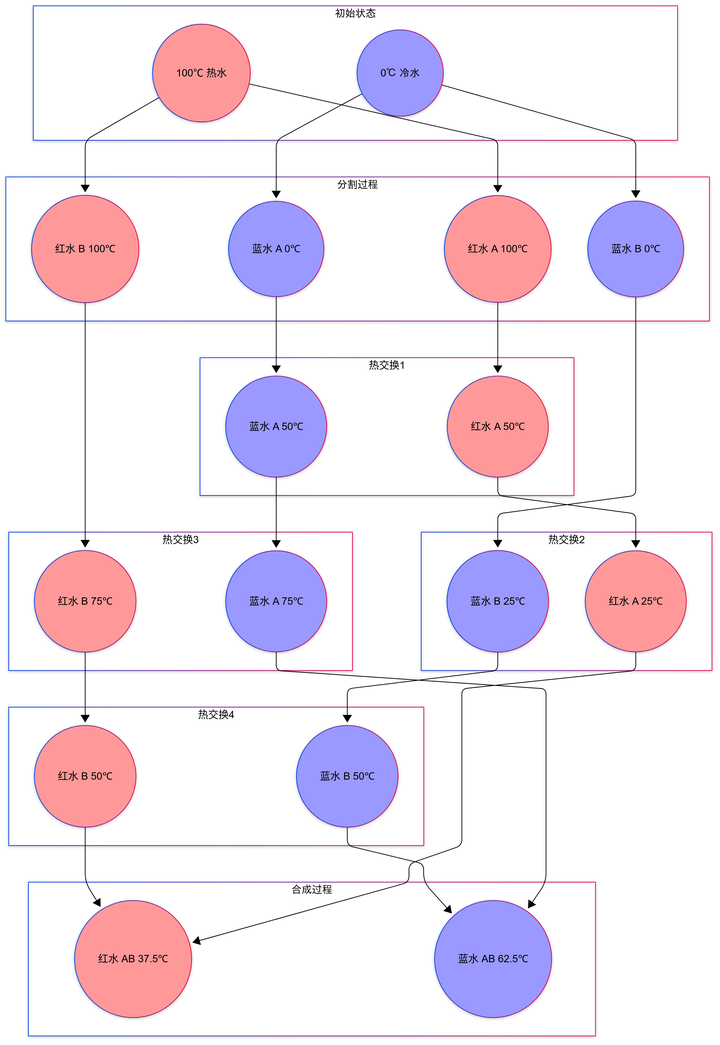
注意这两杯水是有染色的, 是真正的交换了热量, 并非交换了水的位置

合法的方案必须将蓝水里所有的分子都加热才行, 一个分子也不能少

分成两份居然夺走了 62.5% 的热量, 比直接混合的 50℃ 强得多。

如果分成 10 份经过同样的操作能达到 82.38℃, 分成 100 份会达到 94.36℃, 分成 10000 份会达到 99.44℃。

太神奇了！

看来是切的越多, 逐份加热再混合以后掠夺的热量越多。

那么分成无限份能夺走全部的热量吗?

考虑如下递推方程:

$\begin{aligned} a_{i,j} &= \dfrac{a_{i,j-1} + a_{i-1,j}}{2}\\ &=\frac{100}{2^{i+j-1}}\sum _{k=0}^{i-1} \binom{i+j-1}{k}\\ &=100-100\binom{i+j-1}{i} \, _2F_1(i,i+j;i+1;-1)\\ S&=\frac{1}{n} \sum _{i=1}^n a_{n,i}\\ &=\frac{100}{n}\underset{i=1}{\overset{n}{\sum }}\frac{1}{2^{i+n-1}} \underset{k=0}{\overset{n-1}{\sum }}\binom{i+n-1}{k} \end{aligned}$

我这里只是为了满足你的好奇心，虽然一通爆算展开超几何函数肯定可以, 但其实有更巧妙的解法。

你要证明的是:

$\displaystyle\lim_{n\to \infty }\frac{100}{n}\underset{i=1}{\overset{n}{\sum }}\frac{1}{2^{i+n-1}} \underset{k=0}{\overset{n-1}{\sum }}\binom{i+n-1}{k}=100$

主要难点在内部这个二项式展开怎么求。

但其实不用求, 因为可以直接用正态分布近似。

不妨考虑二项式分布的累积分布函数。

设

$X$

服从二项分布

$B(i+n-1, 1/2)$

则

$\displaystyle P(X \leqslant n-1) = \sum_{k=0}^{n-1} \binom{i+n-1}{k} \left(\frac{1}{2}\right)^{i+n-1}$

即

$\displaystyle \sum_{k=0}^{n-1} \binom{i+n-1}{k} = 2^{i+n-1} P(X \leqslant n-1)$

将这个结果代入原式，得到：

$\displaystyle \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n}\frac{1}{2^{n+i-1}} 2^{i+n-1} P(X \leqslant n-1) = \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n} P(X \leqslant n-1)$

该二项分布的期望是

$\mu = \dfrac{i+n-1}{2}$

，方差是

$\sigma^2 = \dfrac{i+n-1}{4}$

。

该二项分布的正态分布近似为:

$\begin{aligned} P(X \leqslant n-1) &= P\left(\frac{X - \mu}{\sigma} \leqslant \frac{n-1 - \mu}{\sigma}\right)\\ &= P\left(Z \leqslant \frac{2n-2 - i - n + 1}{\sqrt{i+n-1}}\right) \\ &= P\left(Z \leqslant \frac{n-1-i}{\sqrt{i+n-1}}\right) \end{aligned}$

其中

$Z$

服从标准正态分布

$N(0,1)$

。

因此

$\displaystyle \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n} P(X \leqslant n-1) = \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n} P\left(Z \leqslant \frac{n-1-i}{\sqrt{i+n-1}}\right)$

当

$n \to \infty$

时，对于给定的

$i$

有

$\dfrac{n-1-i}{\sqrt{i+n-1}} \to \infty$

。

因此

$\displaystyle P\left(Z \leqslant \frac{n-1-i}{\sqrt{i+n-1}}\right)$

以概率 1 成立

所以

$\displaystyle \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n} P\left(Z \leqslant \frac{n-1-i}{\sqrt{i+n-1}}\right) = \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n} 1 = \lim_{n\to \infty }\frac{n}{n} = 1$

即证

$\displaystyle \lim_{n\to \infty }\frac{1}{n}\sum_{i=1}^{n}\frac{1}{2^{n+i-1}} \sum_{k=0}^{n-1}\binom{i+n-1}{k}=1$

呃, 所以数学上是成立的.........

那么物理意义是啥呢?

就是热分子按顺序撞击了所有冷分子, 把自己的能量全给了冷分子............

约等于热水和冷水对撞, 自己内部分子一个都没撞到, 热水分子全部捉对撞到了冷水分子.........

这是什么麦克斯韦家族的新神兽吗?

查看知乎讨论