好不容易看到热榜上有关于宇宙的问题了,来答一下。我小时候也好奇宇宙有没有“外面”,如果有的话外面是什么?如果没有外面的话那宇宙应该是一个什么样的形状?这个问题一直到我大三学了广义相对论之后才搞明白。我先试着向家长解释一下这个问题吧,毕竟给家长讲明白才有可能给孩子讲明白。
先上结论,宇宙有没有外面依赖于宇宙的定义:
1.如果我们说的“宇宙”是指可观测宇宙,那么它是有限的,半径大约 460 亿光年。半径 460 亿光年的那个球面称为视界,视界里面的东西原则上是可以被我们观测的,视界外面的东西目前不可观测(可以理解为它们发出的光还没传播到我们这里,甚至有可能由于宇宙的膨胀永远无法传播到我们这里)。因此,如果“宇宙”是指可观测宇宙,那么它是有“外面”的。既然有外面,那外面是什么呢?答:可观测宇宙外面依然是广袤的宇宙,只不过视界外面无法被我们观测。
2.如果我们说的“宇宙”是指停止暴胀的宇宙,那么它是有限的,半径远大于可观测宇宙的 460 亿光年的视界。这里要解释“暴胀”一词:暴胀是宇宙在其诞生的极早期可能经历的一场剧烈的指数膨胀过程(
秒内尺度可以膨胀超过
倍)。根据暴胀理论,宇宙中会有无数的已停止暴胀的区域,它们就像宇宙中无数个巨大的“泡泡”,我们现在所处的可观测宇宙区域就在某个泡泡里面。因此,如果“宇宙”一词是指停止暴胀的宇宙区域(一个泡泡),那么它是有外面的,泡泡外面是仍在暴胀的宇宙以及其他无数个类似的泡泡。更多关于泡泡的内容可以参考这篇回答:
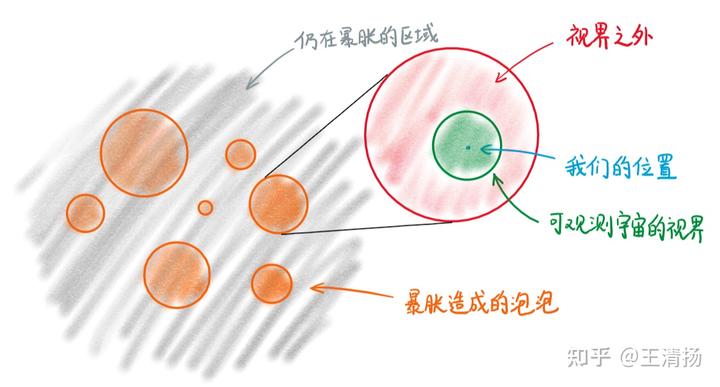
3.如果我们说的“宇宙”是指整个宇宙,包括可观测和不可观测的部分,也包括仍在暴胀的部分,那么当前的宇宙学观测没有告诉我们它是有限的还是无限的。不过,可以肯定的是,根据当前的宇宙学理论,不论整个宇宙是有限的还是无限的,它都是没有外面的。接下来细说:
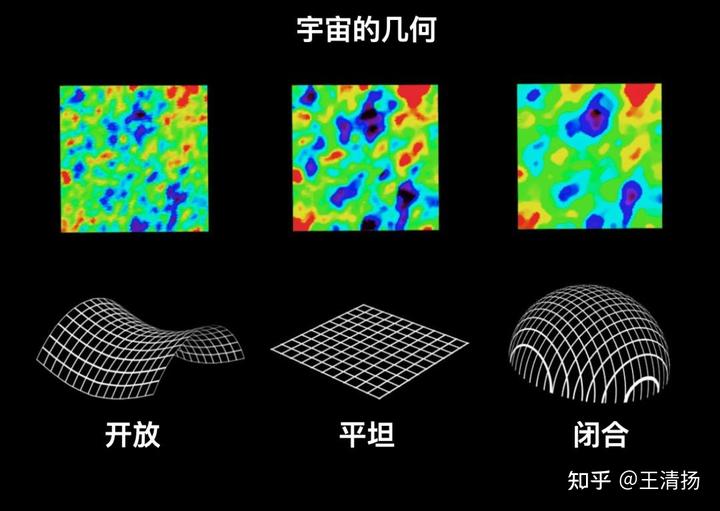
现代宇宙学中有一个重要的假设——宇宙学原理:宇宙在极大尺度上是均匀各向同性的,也就是说我们朝各个方向观测宇宙在极大尺度上的物质分布都会得到相似的结果。在这个假设下,通过数学方法可以证明宇宙的几何形状不是任意的,而是被严格限制的,它和一个被称为曲率 K 的参数有关。①当 K>0 时,宇宙空间的几何形状是一个四维球的三维表面,称为闭合宇宙。这个三维表面的“面积”(即我们宇宙的体积)是有限的,这将意味着宇宙是有限而无界的,没有“外面”。你也许会问,为什么闭合宇宙是有限的却没有外面呢?答:就好比一个三维球的二维表面是有限的,但在此生活的二维生物永远走不出这个球面,即没有外面。②当 K<0 时,宇宙空间的几何形状是一个三维马鞍面,称为开放宇宙。这是一个无限无界的宇宙,也没有“外面”。因此,不论整个宇宙是有限的还是无限的,它都是没有外面的。
看评论区有小伙伴问,当我们不处于球面上,不就可以看到球面的“外面”了吗,为什么还说作为三维球面的闭合宇宙是没有外面的呢?答:这个问题的前提是我们可以不处于球面上,然而我们真的可以不处于这个球面上吗?换句话说,如果空间存在额外的维度,那么我们自然可以说三维球面有“外面”,就好比我们在三维空间中说二维球面有“外面”。但是,目前没有任何迹象表明空间有足够大尺度的额外维度(对撞机实验可以检验这一点,如果有足够延展的额外维,那么对撞机实验中将会丢失一些粒子跑到额外维中去,实际上没发生这种事)。因此,即使额外维存在,它也只蜷缩在一个很小的尺度上,就像弦理论那样。综上所述,没有任何迹象表明宇宙中的一切可以脱离这个三维曲面,所以我们说作为一个三维曲面的宇宙模型是没有外面的。
再说两句题外话,实际上前面说的这个曲率参数 K 是可以通过观测宇宙微波背景辐射(CMB)去测定的。也就是说,原则上我们可以通过测量 K 是大于 0 还是小于 0 去判断宇宙是有限的还是无限的。然而,宇宙微波背景辐射(CMB)的实际观测结果表明:K 非常非常接近 0,以至于我们无法判断它是大于 0 还是小于 0。这是一种处于闭合和开放之间的临界情况,它的几何形状就是我们熟悉的三维平坦空间。所以很遗憾,以目前的观测精度,我们无法确定宇宙到底是有限的还是无限的。(注:K 恰好非常接近 0 不是巧合,是极早期宇宙暴胀的必然结果,感兴趣可以参考下面这篇回答:
先写这些吧,如果看的人多的话我再写写该怎么和孩子解释宇宙有没有外面这个问题。我之前写过一篇怎么向孩子介绍宇宙起源的回答,可惜没多少人看,把链接放这里吧:

