这个问题是我提的,但是好像没什么人回答。
我来抛砖引玉简单写一个——利用代数拓扑来证明彭罗斯三角形在现实不可能存在。
一、埃舍尔的艺术作品
在正式回答之前,我们先来认识一位荷兰版画艺术大师——莫里茨·科内利斯·埃舍尔(Maurits Cornelis Escher,1898-1972),他以其独特的视觉错觉和几何形式的作品而闻名,从中可以看出分形、对称、密铺平面、双曲几何、多面体、拓扑等数学概念的形象表达。

他的画作常常展现出悖谬的空间结构,让人仿佛置身于一个逻辑自洽却无法在现实中实现的世界。








关于埃舍尔的作品,值得说道的数学内容有很多(如果我有空可以专门写几期回答),但我们今天关注的重点就在于那些不可能的建筑(impossible constructions)。
细心的你一定发现了,埃舍尔的作品里有许多优美的几何建筑,但仔细观察又会察觉到明显的违和感。例如,上面最后一张画作《瀑布》(Waterfall, 1961)里,瀑布既像是从上而下坠落,又像是从下往上循环,这种现象显然违背了能量守恒定律,它是不可能存在的。
《观景楼》(Belvedere, 1958)里,建筑第二层和第三层一个是纵向拓展而另一个是横向拓展的,且支撑楼面的石柱前后关系也发生了改变。同时,也请不要忽视画面左下角的那位小男孩,他手中拿着的方块也是不可能在现实世界中存在的。

这些画作都是利用二维图像,被人类自然理解成三维物体的投影时产生的视觉错觉,它不能作为实体物体存在于三维空间中。
二、不可能图形
除了埃舍尔的经典画作之外,还有其他的不可能图形的例子:
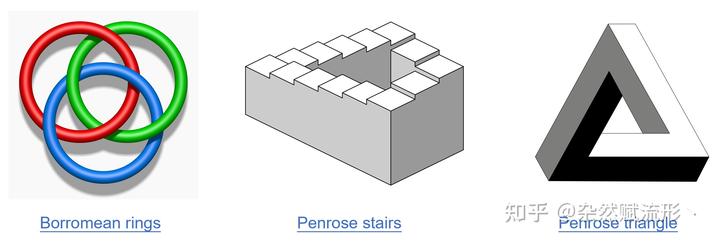
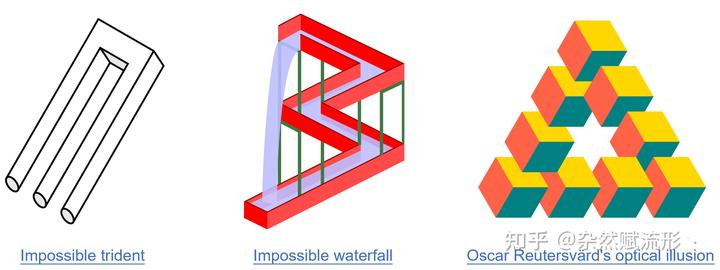
例如彭罗斯三角形(Penrose Triangle),它看似是一个封闭的、连续的三维结构,但在现实中却无法真正构造出来。不过值得一提的是,通过视觉错觉,我们在现实世界里是可以在某一个特定角度观察到彭罗斯三角形结构的,例如以下的旋转模型就展示了错觉如何发生:
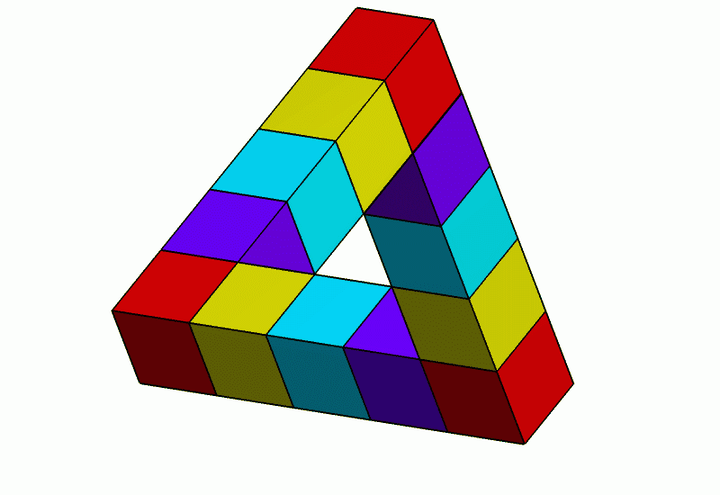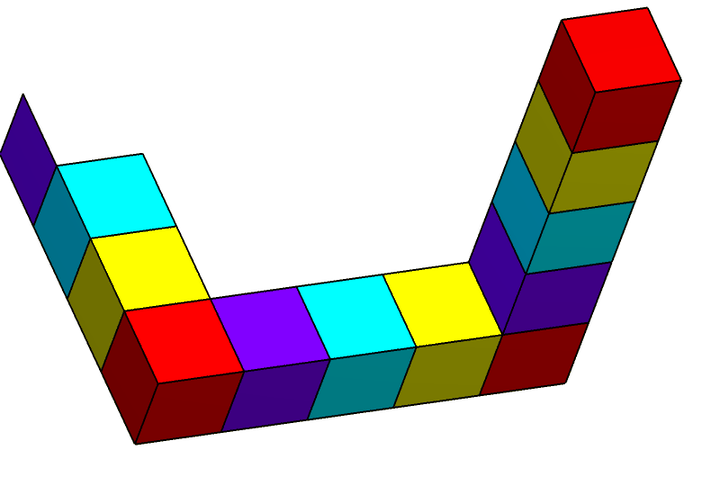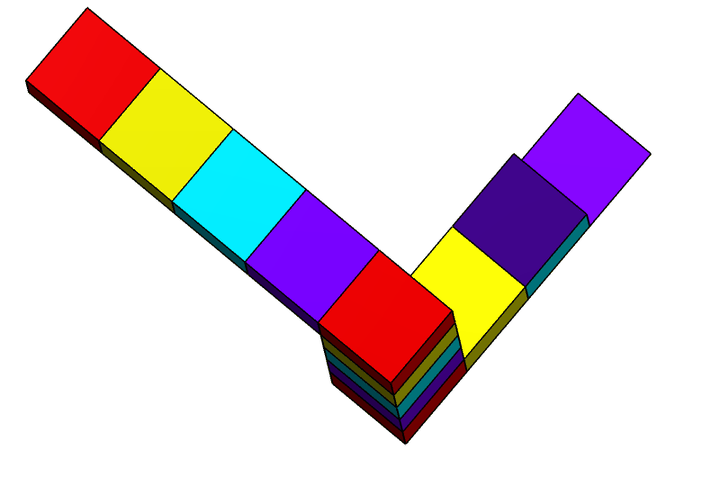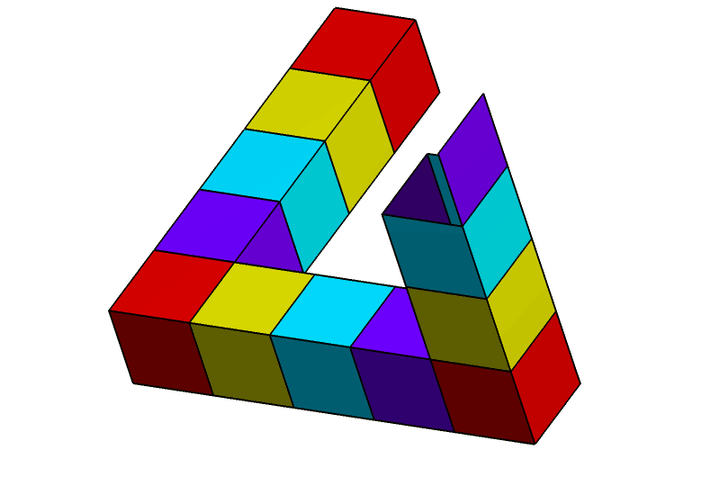

著名游戏《纪念碑谷》里也大量运用了类似的视觉错觉,构建了很多复杂的游戏迷宫,


但你有没有想过,这些不可能物体的「不可能性」仅仅源自我们的感知,我们应该如何利用数学语言严格证明它在现实世界里不可能存在呢?
故事才刚刚开始。
三、彭罗斯的证明思路
这些不可能图形的共同特点是,局部看起来符合三维几何规则,但整体却构成了一个矛盾的结构。
数学家彭罗斯就曾在 1992 年的一篇文章里讨论如何用数学语言描述这些不可能物体,他在其中借助了代数拓扑中的上同调(cohomology)理论来分析其结构[1][2]。

所谓代数拓扑,是利用抽象代数的工具来研究拓扑空间,其基本目标是通过寻找拓扑空间的具有代数结构的不变量,从而将拓扑空间分类。而上同调则是一种刻画拓扑空间全局性质的工具,可以看作是一种对拓扑空间赋予代数不变量的方法。尽管代数拓扑的内容较为抽象,但我们接下来的证明并不需要具备太多代数拓扑的知识,它的思路非常清晰易懂。
以彭罗斯三角形为例,我们先简单介绍一下思路(不需要任何初中以上的数学)。
我们可以把彭罗斯三角形绘制在平面上的一个环形区域,显然这个区域不是单连通的(即在此空间中,所有闭曲线不一定能连续地收缩至一点),我们把此区域记为 ,它就是我们要研究的拓扑空间。
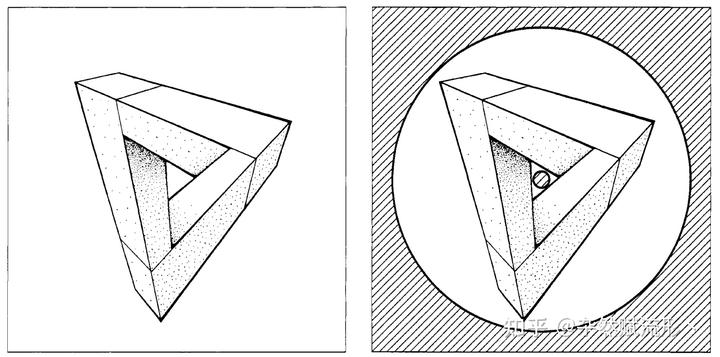
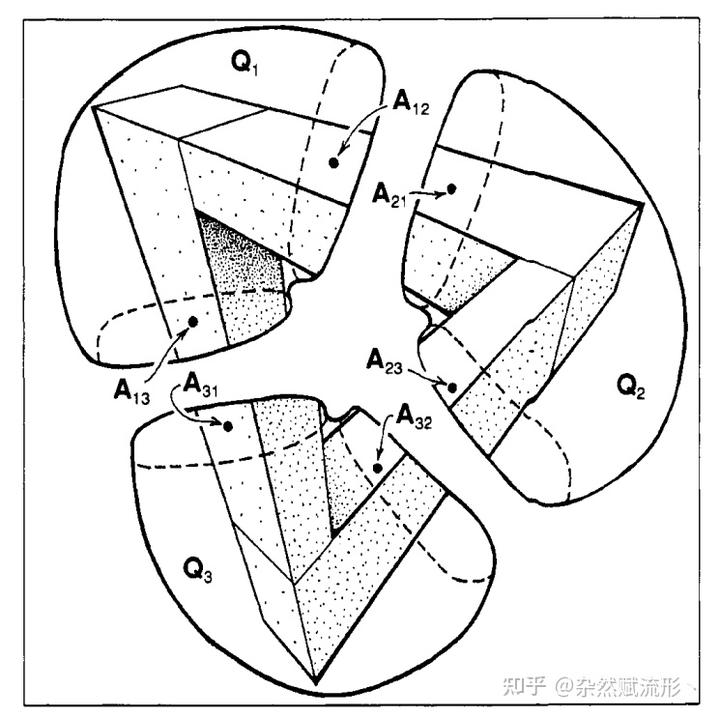
进一步,我们可以把拓扑空间 分解为三个部分
,它们重叠的部分粘在一起便可恢复
。相应地,彭罗斯三角形也被分割成了三个 L 形部件,显然它们各自都是可以在现实世界里真实存在的。
其中 部分的点
和
部分的点
重叠。
部分的点
和
部分的点
重叠。
部分的点
和
部分的点
重叠。
但这里仍然存在一个含糊不清的地方,因为我们绘制的是一个 2D 透视图,它实际上代表的是 3D 物体在 2D 平面中的投影。我们无法确定真正的 3D 彭罗斯三角形(假设它能存在)离我们的眼睛真实距离是多少。
如下图所示,某两个真实存在的物体 ,它们在
上的投影是相同的,但它们离我们人眼的距离不同。
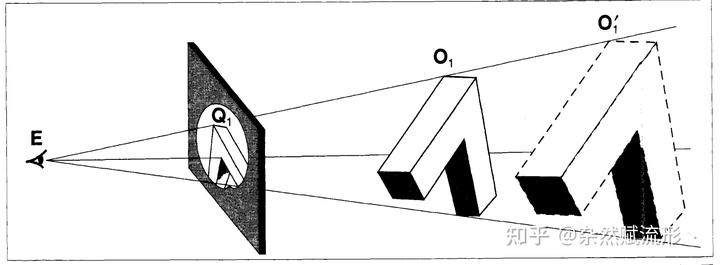
我们把真实物体距离人眼的距离记为 ,显然它可以取任意的正实数。当
增大时,物体的大小按相应比例也会放大。所有正实数的集合构成了群
,配备数的乘法作为群运算,单位元是
。这里的
我们把它记为彭罗斯三角形的歧义群(ambiguity group),因为它表征了不可能图形的歧义所在。
现在我们假想有一个真实存在的三维物体 ,我们在
上画的图就代表它。同理,也假想真是物体
,分别对应
。
由于存在上述提到的歧义,我们无法确定对应 的
上的点离我们的真实距离
是多少。相应地,我们也无法确定对应
的
上的点离我们的真实距离
是多少。我们把这两个距离之比定义为
,即
注意
并不依赖于我们选择的点
和
的具体位置,只要我们选择的是对应到初始彭罗斯三角形上同一个点分解后对应的两个点,我们就会得到相同的
。同理,对于其他点我们也可以定义类似的量:
且有
。如果我们将
视为更远处(更近处)的物体,那么它上面的点离人眼的距离就会增大(减小),比例因子记为
。那么
就会被替换为:
如果彭罗斯三角形是真实存在的,就意味着所有的
,即互相重叠的点离人眼的距离相同,这样才能构成自洽的物体。我们可以调整
的位置,比例因子记为
,那么自洽条件要求:
也即
如果不存在满足上述自洽条件的
,那么我们就证明了该物体不可能存在。
四、上同调理论的解释
这里我们把第三节中的思路用 Čech 上同调的语言重新叙述一遍。
对于拓扑空间 ,即
,每一个子集
和任意两个子集的交集
都同胚于一个三维实心球体
。
0-cochain 给每个子集 分配一个正实数
,对应的是缩放因子。而 1-cochain 对每个
分配
。
实际上是一个 cocycle。如果存在
使得
成立,那么 cocycle 又被称为 coboundary,否则称其为非平凡的 cocycle,此时它就对应一个拓扑非平凡的结构,也就是不可能图形。
而 提供了 coboundary freedom。如果两个 cocycle 可以在此变换下互相转化,那它们是等价的。在此等价关系下,我们就得到了上同调群
的一个元素。而所有的 coboundary 代表上同调群
的单位元。非单位元则对应不可能图形。我们上面的所有讨论,浓缩起来就是一句话:cocycle
是否对应
的单位元?
Remark: 彭罗斯在文章里提到的第一上同调群在严格数学定义中,是基于开覆盖
的 Čech 上同调。但是由于开覆盖
中所有元素都同胚于
,其拓扑结构足够简单,使得我们的计算实际上仅依赖于拓扑空间
本身,即
。
我们考虑 evaluation map ,选择一个路径:
形成一个封闭的循环,我们就得到了 1-cochain 的乘积
,它实际上是检测 1-cochian 是否形成一个 coboundary。如果我们沿着此三角循环移动时,所有的变换应该抵消最终回到单位
。反之,如果
,这说明整个循环中存在某种扭曲或不一致,那么
就是一个非平凡的 cocycle。
利用我们最开始关于 的分析,我们可以得到
现在我们根据这个表达式再重新回头看一下彭罗斯三角形,

我们固定住 距离人眼同一距离,即
,
- 当我们聚焦于
时,根据传统的透视关系,我们知道
相比
距离人眼更近,即
;
- 同理,当我们聚焦于
时,根据传统的透视关系,我们知道
相比
距离人眼更远,即
。
因此,在 的表达式里,一个因子等于 1,另外两个因子大于 1,所以
,于是
是一个非平凡的 cocycle,彭罗斯三角形不可能在现实生活中存在。
五、写在结尾
彭罗斯三角形表面上只是一个简单的视觉错觉问题,但是通过上同调的语言,我们能够严格证明它在三维空间中的不可能性。这种方法其实不是数学上的炫技,而是一种强有力的工具,它能在更一般的情况下识别「局部合理但全局矛盾」的结构。
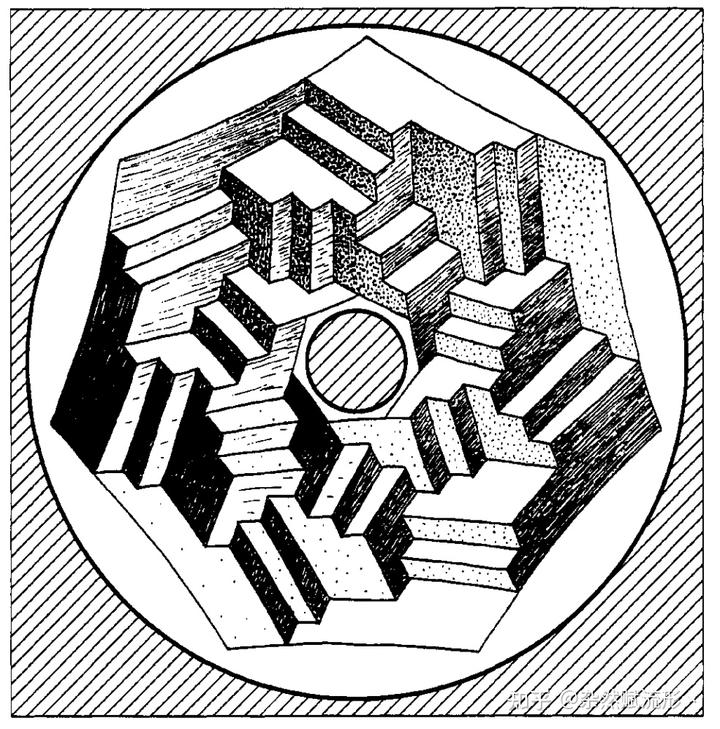
除了彭罗斯三角形之外,借助上同调的语言,我们还能分析其他「不可能图形」,例如彭罗斯原文里还提到了另一个不可能图形,它的讨论相对更简单一点,这时候它的歧义群仅仅是 ,
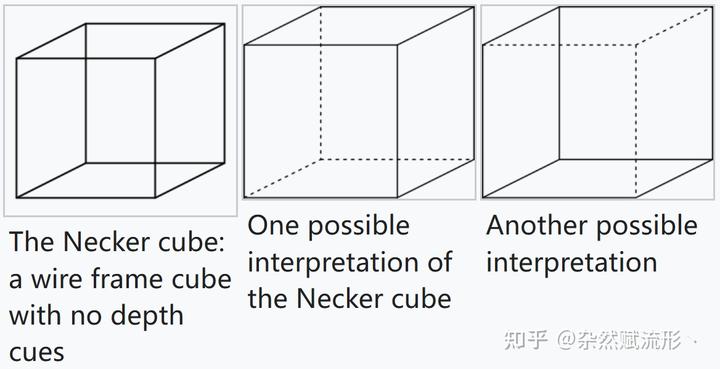
歧义的一个著名例子就是 Necker 方块(下图左),它没有明确给出任何立体信息,只有模棱两可的解释(下图中、下图右)
另外还有彭罗斯砖块,

证明它是不可能图形也很简单,逻辑和我们上述讨论是一致的,区别仅仅在于我们讨论的是上同调群 ,此时
都是
的元素(即它们仅取值
或
)。
对此感兴趣的同学可以自己尝试去证明。

