格林公式阐述了一个简单而又重要的物理事实,守恒。
比如,打台球:

它的能量守恒是这样的:

击球的能量产生在桌面上,所以调整一下守恒式,就得到了格林公式:
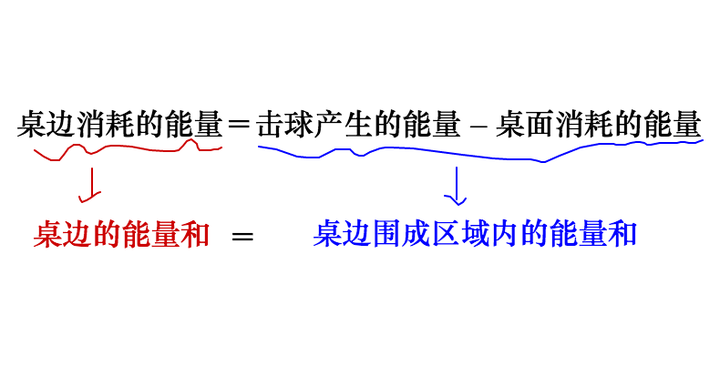
下面让我们一步步建立物理模型来解读上面的描述,并推导出格林公式。
本人不才,下面的物理都主要重视直观理解,不求严格性,恳请物理大咖指点纠正。
1 关于旋转的物理问题
在剑桥大学的小路上,正在思考的乔治·格林被一个学生拦住了,学生愁眉苦脸的说:“老师,您好,有个问题我一直没有想清楚,您帮我合计合计。”
学生继续说道:“这个问题就是,我应该怎么去分析水流中,螺旋桨的做功情况?”

“这是一道应用题,”格林眉毛一拧:“肯定是先建模啊。”
2 模型的建立
首先,水流作用到螺旋桨上,表现为力,因此先把水流转为力场
:

把这样的螺旋桨:

抽象一下,放入到力场中去,就会旋转起来(手动移动下螺旋桨的位置,还会发现在不同的位置旋转速度不一样):

此处有互动内容,点击此处前往操作。
进一步简化一下,我们只研究其中某一个点的在旋转中的做功:

等价于研究某一点在圆形路径上的做功:

格林说:“问题就被转化为了沿路径做功了,我们看看物理层面怎么解答。”
3 物理的解答
3.1 旋转方向与有向路径
首先,规定逆时针旋转为正方向:
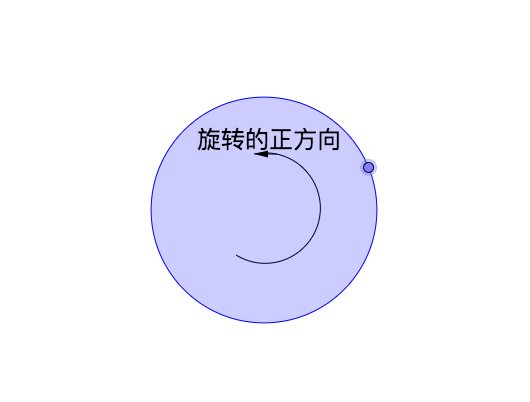
旋转有了方向之后,此点走过的路径也就有了方向,我们称为“有向路径”。
根据旋转的正方向,就可定义点走过的路径的正方向:
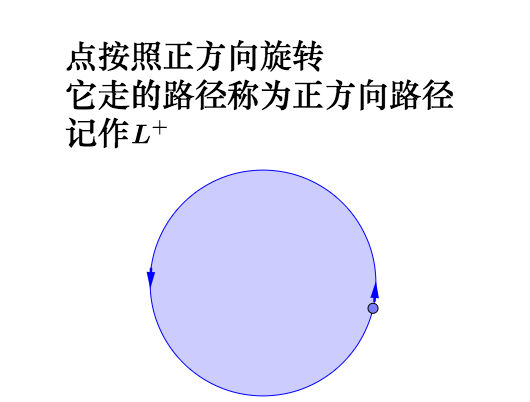
点要是反着转,那么走过的路径自然就是
。
3.2 做功分析
根据微积分的思想,我们把路径切成无数个微小的曲线段:

根据我们已知的两个知识(已知的意思,其实是我不想解释了):
- 根据微积分“以直代曲”的思想,这些微小的曲线段可以用切线来代替
- 根据物理知识,我们知道,力只在路径方向做功
结合上述两点,我们可以得到,每个微小的曲线段上做的功为:
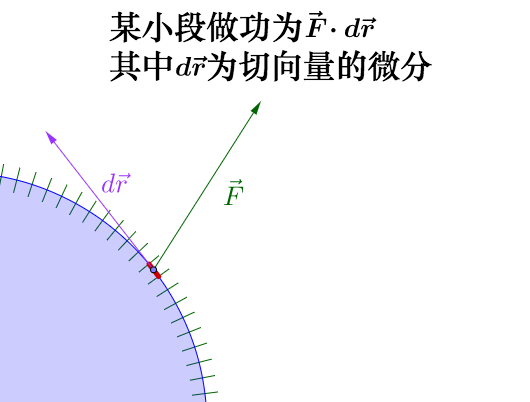
那么,很明显,整段封闭曲线做功可以表示为如下:
“哇,清晰多了!”同学搓搓手,递上一只大前门香烟:“老师,可是怎么计算呢?”
格林抽出笔来,刷刷地写道:“就这么算!”
4 数学计算
4.1 矢量形式转为标量形式
矢量形式
不太好计算,让我们转为标量形式。
根据我们一元微积分的知识,我们知道
在
方向的分量为:

那么,有
和
,所以,
,所以:
4.2 非常简单的加减运算
我们给出一个简单的力场,这个力场的特点是:
- 只有水平方向的力
- 在同一个垂直高度上,力的大小一样
- 随着垂直高度的增加,力逐渐减小
画出来就是这样的(矢量的方向表示力的方向,矢量的长度表示力的大小):
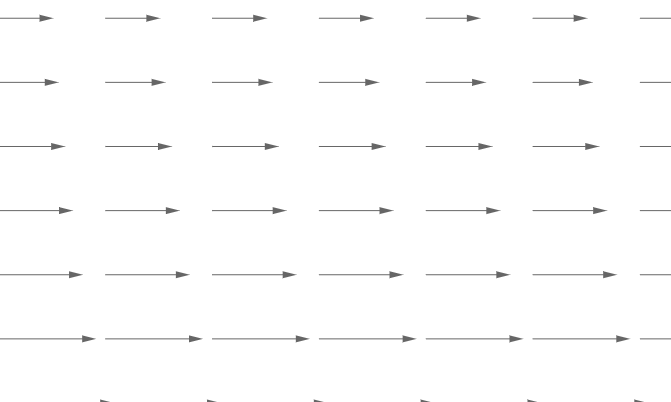
计算在此力场中,某点围绕正方形路径一圈所做的功,已知:
- 正方形边长为 3
- 上边受力大小为 1,下边受力大小为 4
- 力与左右两边垂直,所以在这两边不做功
如图:
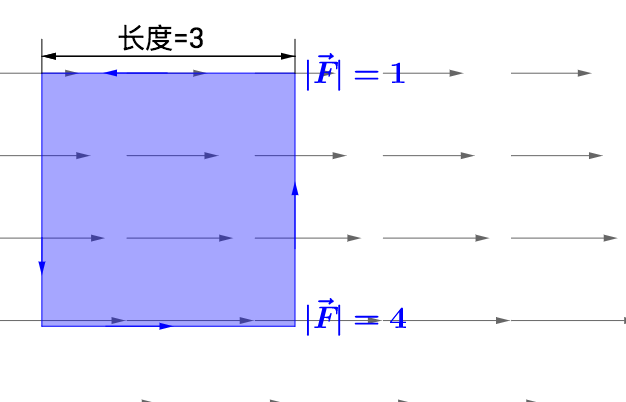
所以,算出某点围绕正方形路径一圈所做的功为:
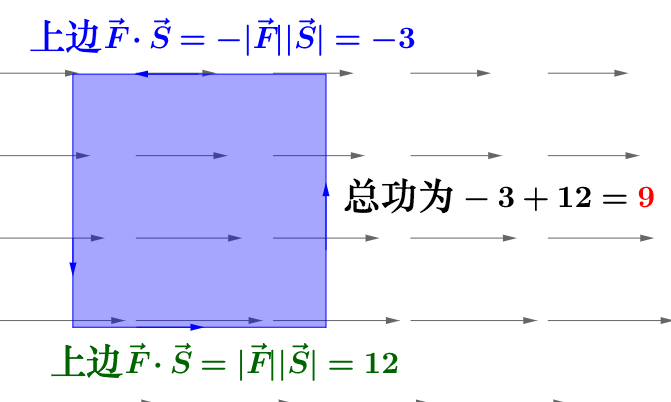
把正方形均分为 9 宫格,每块都是变长为 1 的正方形,每条正方形的边所在力场的大小我也标注在图里了:
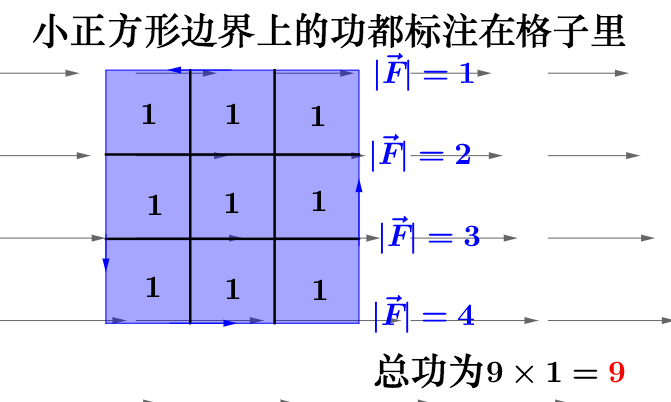
可见,两种运算方法得到的结果都是一样的。
这是一个简单的演算,可以推广为,任意的路径边界上的功,等于路径围成的区域内的所有微分矩形(矩形也符合“以直代曲”的微积分思想)的边界上的功之和:
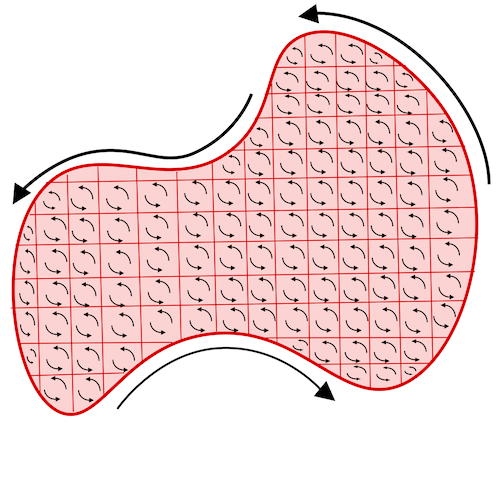
这也就是我刚开始说的守恒,虽然功和能量还不是一回事,不过也算紧密相关,允许我这个物理民科这么去直观理解。
4.3 计算微小矩形边界上的功
怎么计算微分矩形上做的功呢?让我取一个微分矩形出来,我把矩形的边和顶点、以及矩形的区域都标注出来了:
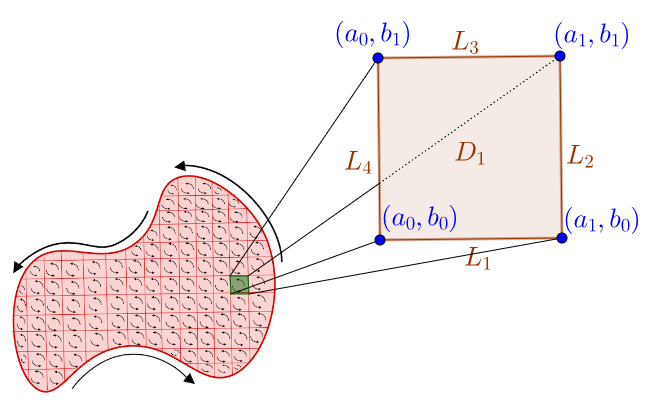
下面是代数推断了,我觉得过程还是很清晰明了的。
首先,注意到在
上
为 0(因为
方向没有变化),
上
为 0,然后我们继续推下去:
微分矩形的边界做功求出来了,结合我们之间的结论,边界的做功=微分矩形做功之和我们可以得到最终的结论:
其中
为
围成的区域。
同学之前听得屏息凝视,现在才有机会长出了口气:“真是精彩啊!”
格林反问道:“你知道
会得到什么吗?”
是法向量。
5 通量
代表力在运动方向做功,但是力并不会在与运动的垂直方向做功,那么
代表了什么?
如果把
看作流速,或者电流密度,那么
就在流体力学、电磁学中被称为通量。
关于通量更详细的可以看我另外一个回答 散度和旋度的物理意义是什么 ,其中回答了为什么是法向量方向。
比如,对于我们头顶上的太阳:

我们要计算穿过(包括射出和进入)太阳表面的能量总量:
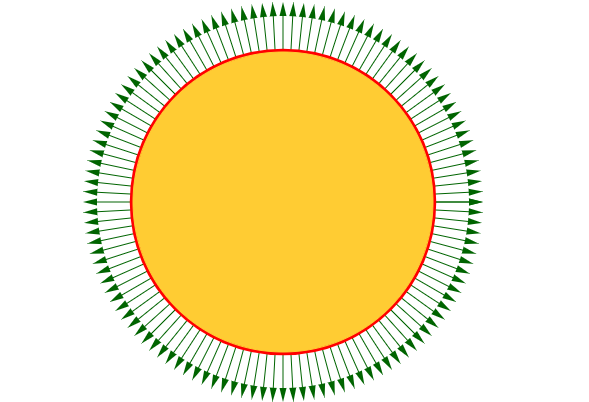
这就是通量,记作:
太阳内部时时都在发生核聚变,以及其他的能量活动:

根据能量守恒,内部的能量总量,必然等于穿过太阳表面的能量总量。
也就是说,通量和内部能量总量相等。
定了这个基调之后,然后按照之前分析做功的方式,最终我们可以得到:
格林说完之后,突然发现,自己发现了不得了的东西,对于数学有重要的意义,相当于把封闭曲线的线积分转为了二重积分。所以,赶快去发表论文吧。
6 总结

乔治·格林(1793 — 1841),英国科学家,格林公式的发明者。
根据不同的物理意义,格林得到了两种格林公式的形式:
做功的形式(电磁学、流体力学也可以把
看作流速,下面就称为环流量):
通量的形式:
旋度和散度也出现在公式中了。
本文轻度调侃了乔治·格林,并非不敬。在我眼中科学家才是真正的英雄,希望我可以写出这些科学大咖风采的一二,借用《红楼梦》中的一句话,但使大家知道“科学界历历有人”。
更多内容推荐马同学图解数学系列

