初中时曾在《重难点手册》上看到了一个证明“所有的三角形都是等边三角形”,看完后我震惊了好久没能找到破绽,直到自己动手作图尝试了一下(当年书上没有提供答案)。
在此不得不感慨,纸上得来终觉浅,绝知此事要躬行。
这道题目是这样的:
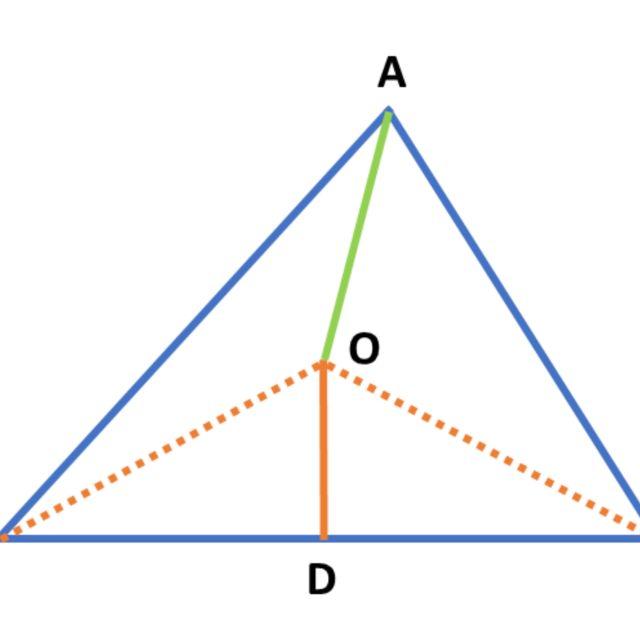
根据示意图,对于一个任意三角形
,通过其一个顶点 A 做
的角平分线 AO,它与边 BC 的中垂线相交于点 O,而且点 D 是 BC 的中点。下面开始证明 AB=AC
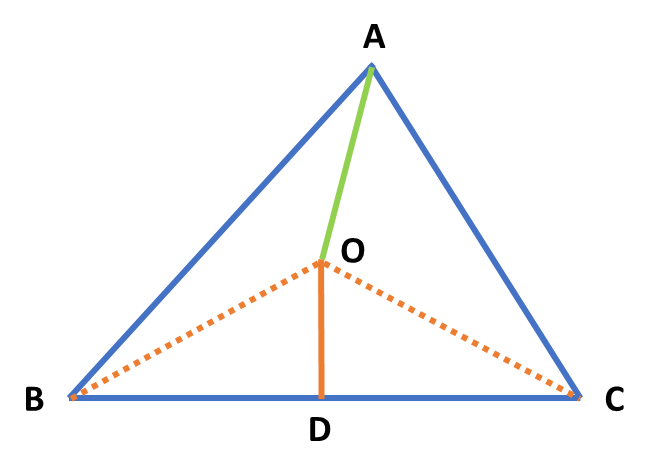
为了证明 AB=AC,我们需要一些辅助线。连接 OB 以及 OC,并且通过 O 点做 AB 和 AC 的垂线,分别相交于点 E 和点 F。如下图所示:
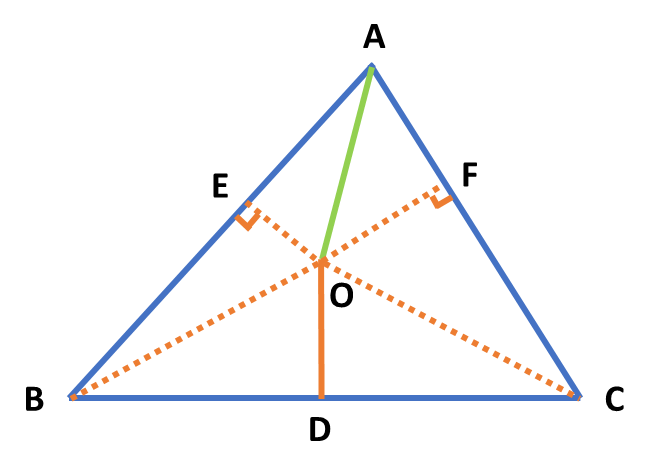
我们先来证明
(三角形 OAE 和三角形 OAF 全等)
由于 AO 是角平分线,所以
这两个三角形共用 AO 这条边
这两个三角形都是直角三角形(
,
)
所以我们可以得出
(确实全等)
那么就有 AE=AF
下面我们来证明
(三角形 OEB 和三角形 OFC 全等)
因为
所以 OE=OF
然后因为 OD 是 BC 的中垂线,所以 OB=OC
最后这两个三角形都是直角三角形 (
,
)
所以
(确实全等)
那么我们就有 BE=FC
( 说实话,我是没有预料到这么多人说这是角边边不能全等……
角边边确实不能用来判定两个非直角三角形全等,但是可以用来判定两个直角三角形全等,这是 HL!
而这里,是直角三角形,所以证明没有问题
如果你依然不能理解的话,我有两个建议
- 请复习一下全等三角形的部分
- 请自行运用三角函数来判断一下 )
最后证明 AB=AC
因为 AB=AE+BE, AC=AF+FC
而且 AE=AF, BE=FC
所以 AB=AC
然后我们通过类似的方法,通过另一个顶角做角平分线的方法,可以证明 AB=BC=AC
由于这是一个任意三角形,所以我们可以得出任何三角形都是等边三角形。
揭秘开始:
当时的我,一开始没有当回事。但是当我一遍又一遍地审阅其中的证明时却傻眼了——我居然没看出问题!此外,对于这道思考题,《重难点手册》居然还没有解答!
无奈之下,我拿出了直尺和圆规,决定亲手作图来看看其中的玄机。一画完图,我就意识到了其中的玄机——第一步就把我给糊弄了,非等腰三角形的角平分线和对边的中垂线的交点,并不在三角形内部,而是在三角形外部!(而对于等腰三角形,则这两条线重合)
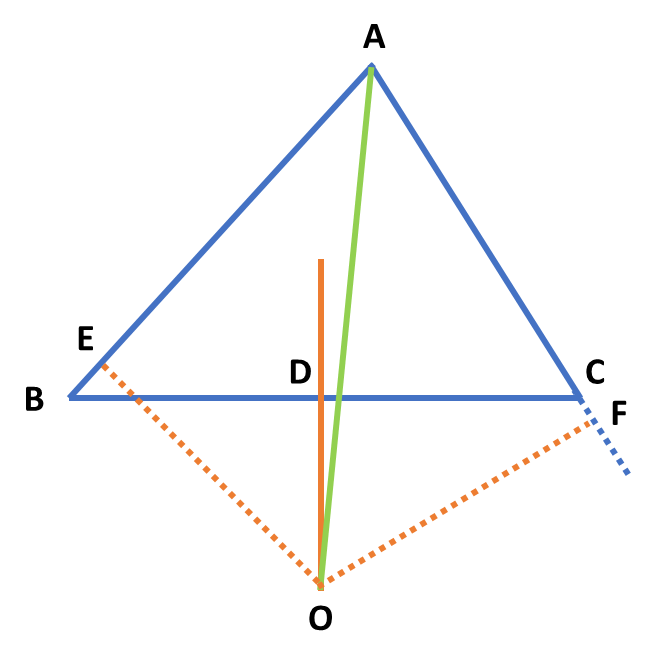
所以后续就是,确实 AE=AF,确实 BE=FC
但是 AB=AE+BE,而 AC=AF-FC
所以
——而 BE 和 AB 的比值大概可以反映偏离等腰三角形的程度吧
并不是所有的三角形都是等边三角形
实际上这个证明方法可以被用来作为反证法,用于证明
为何非等腰三角形的角平分线和对边中垂线交点在三角形外;
为何三角形的角平分线一定在垂线和中线之间。
我很感谢这道题,很感谢它没有给我答案,从而逼迫了我自己去找寻这么有意思的事情。