「双曲函数」为什么要叫双曲函数？到底应该怎样定义双曲函数？

南中国海的一条鱼，看到收藏动态别忘了到我的收藏夹里去看一看。

如果问“山为什么叫山？”、“水为什么叫水？”，我们只能说，这是中国人（汉族人）长期语言交流实践约定俗成下来的。

但如果问“双曲函数为什么要叫双曲函数”，那么回答就不一样了，我们来看一下这个词，它叫“双曲函数”，前两个字是“双曲”……这很容易让我们联想到中学时学过的一种圆锥曲线——双曲线。“双曲函数”和“双曲线”两个数学名词中都有“双曲”这两个字，这绝不是巧合。

说说双曲线

直观上讲，双曲线就是“两条曲线”的意思，实际上是因为按照双曲线的定义，相应的图形并不是“连续”的。这样做个比喻，如果没有地球，地是平的，并且这个平地是一个没有边界的大花园，而花园中有一个双曲线花园小路，那么在其中一支小路上行走的人无论怎么走都不会走到另一支小路上。直观上看，真的像是“两条曲线”，所以这个图形就被称作是“双曲线”了。然而不是随便的两条永不相交的曲线都能叫“双曲线”。双曲线有着严格的定义：平面上到两点距离之差等于一个比两点距离小的非零定值的点的集合称作双曲线。

若双曲线的实轴与

$x$

轴重合，则双曲线的方程是

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$

，其中

$a^2+b^2=c^2$

，

$c$

是定义中所述的两点之间的距离的一半，这两个点被称作焦点，而

$c$

称作半焦距。

值得一提的是，反比例函数的图象也是双曲线，反比例函数是形如

$f(x)=\frac{k}{x}$

（

$k\neq0$

）的函数，而曲线

$y=\frac{k}{x}$

则是双曲线。学过二次型应该知道，曲线方程

$y=\frac{k}{x}$

可化为

$xy=k$

，并进一步化为矩阵乘法的形式

$(x, y)\left(\begin{matrix}0&\dfrac{1}{2}\\\dfrac{1}{2}&0\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=k$

对方程左边做二次型的正交变换，得（

$x, y$

仍满足

$xy=k$

）

$(x, y)\left(\begin{matrix}\dfrac{\sqrt{2}}{2}&-\dfrac{\sqrt{2}}{2}\\\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}\end{matrix}\right)\left(\begin{matrix}1&0\\0&-1\end{matrix}\right)\left(\begin{matrix}\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}\\-\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}\end{matrix}\right)\left(\begin{matrix}x\\y\end{matrix}\right)=2k$

取

$(u, v)=(x, y)\left(\begin{matrix}\dfrac{\sqrt{2}}{2}&-\dfrac{\sqrt{2}}{2}\\\dfrac{\sqrt{2}}{2}&\dfrac{\sqrt{2}}{2}\end{matrix}\right)$

，

则方程将变换为

$(u, v)\left(\begin{matrix}1&0\\0&-1\end{matrix}\right)\left(\begin{matrix}u\\v\end{matrix}\right)=2k$

，即

$u^2-v^2=2k$

，这说明反比例函数图象确实是双曲线，顺时针旋转

$45°$

后实轴在

$x$

轴上。

双曲函数和双曲线的关系和双曲函数的定义

事实上，双曲函数就是借助双曲线定义的，不过这里的双曲线不是随便的一条双曲线，而是实轴在

$x$

轴上的标准双曲线，即双曲线

$x^2-y^2=1$

．六个双曲函数都是类比三角函数定义的。首先我们来看三角函数的定义：

设点

$P$

是圆

$x^2+y^2=1$

上的一个从点

$(1, 0)$

出发的动点，

$t$

的绝对值为点

$P$

运动的路程，若

$P$

逆时针做圆周运动则

$t>0$

，若

$P$

顺时针做圆周运动则

$t<0$

，则各个三角函数定义为：

正弦：

$y=\sin t$

余弦：

$x=\cos t$

正切：

$\frac{y}{x}=\tan t$

余切：

$\frac{x}{y}=\cot t$

正割：

$\frac{1}{x}=\sec t$

余割：

$\frac{1}{y}=\csc t$

实际上，三角函数也被称作“圆函数”，之所以称作三角函数，乃是因为三角函数可以用于解三角形。三角函数的参数是任意角，而数学中表示任意角的方法是弧度制，即一个角当其作为圆心角的时候其所对应的弧长与半径之比为这个角的弧度。

那么，双曲函数既然是通过类比三角函数定义而来的，那么第一件事就是应当明确一下双曲函数的参数。首先，由于双曲线有两支，不像圆一样，因而我们只考虑其中的一支。在定义双曲函数的时候采用的是双曲线

$x^2-y^2=1$

的右支。其次，我们希望双曲函数的参数能和三角函数“一样”，但从点

$(1, 0)$

到双曲线上一点间的弧长很难求出来，既然弧长很难求出来，那么可以找另一个用来充当双曲参数的变量。

我们发现，弧长为

$s$

的圆弧，其所对应的扇形的面积是

$\frac{1}{2}rs$

，当

$r=1$

扇形面积就是

$\frac{1}{2}s$

。这也就是说，三角函数的参数，既是弧长，也是扇形面积的

$2$

倍。

因而我们用“面积二倍”的方法定义双曲函数的参数，也就是双曲角：连接原点与双曲线右支上的一点

$(x, y)$

的直线，点

$(x, y)$

到点

$(1, 0)$

之间的双曲线弧段，以及从原点到点

$(1, 0)$

之间的线段所围成的图形的面积的

$2$

倍（当

$y>0$

时面积取正数，当

$y<0$

时面积取负数）为点

$(x, y)$

所对应的双曲角的大小。若记双曲角为

$t$

，则各个双曲函数的定义是：

双曲正弦：

$y=\sinh t$

，函数名读作 /sintʃ/

双曲余弦：

$x=\cosh t$

，函数名读作 /kɔʃ/

双曲正切：

$\frac{y}{x}=\tanh t$

，函数名读作 /tæntʃ/

双曲余切：

$\frac{x}{y}=\coth t$

，函数名读作 /kɔθ/

双曲正割：

$\frac{1}{x}=\text{sech }t$

，函数名读作 /setʃ/

双曲余割：

$\frac{1}{y}=\text{csch }t$

，函数名读作 /'kɔsetʃ/

图中阴影部分面积的 2 倍就是双曲角，若这个阴影在 x 轴下方，则双曲角是负数。

P. S.：很多课本都是直接用自然指数函数给出双曲函数的定义，这个定义过于粗暴，以至于让人很难理解为什么双曲函数叫“双曲函数”。实际上不应该根据自然指数函数给出定义，而是应该根据双曲线给出定义。

P. S.：有些资料上把这六个函数分别简写作 sh, ch, th, cth, sch, xh，反正答主不建议这样写，这个不好记也容易混乱，还是在对应的三角函数名后面加个 h 比较好。

计算双曲角

刚刚说了，双曲角是通过面积来定义的，这很容易让我们联想到定积分，因为定积分可以求出图形的面积。所以我们可以通过定积分来计算双曲角的表达式。注意双曲函数都是定义在右支上的，所以有

$x^2-y^2=1\wedge x>0$

根据双曲角的定义，有

$t=2\left(\int_{0}^y\sqrt{y^2+1}\text{d}y-\frac{1}{2}xy\right)$

可验证

$\text{d}\left(\frac{y\sqrt{y^2+1}+\ln(y+\sqrt{y^2+1})}{2}\right)=\sqrt{y^2+1}\text{d}y$

于是有

$t=2\left(\left(\left.\frac{y\sqrt{y^2+1}+\ln(y+\sqrt{y^2+1})}{2}\right)\right|_{0}^y-\frac{1}{2}xy\right)$

$=2\left(\frac{y\sqrt{y^2+1}+\ln(y+\sqrt{y^2+1})}{2}-\frac{1}{2}xy\right)=2\left(\frac{xy+\ln(y+x)-xy}{2}\right)$

$=\ln(x+y)$

有了双曲角的表达式，我们就可以计算双曲线右支上点的坐标和双曲角的关系式，根据

$x^2-y^2=1$

和平方差公式，得

$\text{e}^t=x+y, \text{e}^{-t}=x-y$

所以

$x= \frac{\text{e}^t+\text{e}^{-t}}{2}$

，

$y= \frac{\text{e}^t-\text{e}^{-t}}{2}$

这样根据刚才的计算结果，就可以得出所有双曲函数的表达式

$\sinh t=\frac{\text{e}^t-\text{e}^{-t}}{2}\\ \cosh t=\frac{\text{e}^t+\text{e}^{-t}}{2}\\ \tanh t=\frac{\text{e}^t-\text{e}^{-t}}{\text{e}^t+\text{e}^{-t}}\\ \coth t=\frac{\text{e}^t+\text{e}^{-t}}{\text{e}^t-\text{e}^{-t}}\\ \text{sech }t=\frac{2}{\text{e}^t+\text{e}^{-t}}\\ \text{csch }t=\frac{2}{\text{e}^t-\text{e}^{-t}}$

参数方程

任意一个以原点为圆心的圆的参数方程都是

$\begin{cases}x=r_0\cos t\\y=r_0\sin t\end{cases}$

，一条以原点为端点的射线和所有以原点为圆心的圆相交，交点对应的参数的值是相等的。

那么双曲线是否也有这种特点呢？我们仿照圆的参数方程，建立等轴双曲线的参数方程，即

$\begin{cases}x=r_0\cosh t\\y=r_0\sinh t\end{cases}\\$

显然，我们根据双曲线和双曲函数之间的关系有

$\cosh^2t-\sinh^2t=1$

，进而有

$x^2-y^2=r_0^2$

，这表明我们建立的参数方程的确是等轴双曲线的右支。

同时，我们可以很容易看出

$\begin{cases}x=r\cosh t_0\\y=r\sinh t_0\end{cases}$

（

$r\geqslant0$

）是过原点的射线的参数方程，这说明我们可以通过等轴双曲线的实半轴（虚半轴）的长度建立双曲线的右支的参数方程，参数就是双曲线右支上的点对应的双曲角。

反比例函数图象的实半轴（虚半轴）长度

根据之前我们对反比例函数解析式

$y=\frac{k}{x}$

的等价变换

我们知道，双曲线

$xy=k$

的实半轴长是

$\sqrt{2k}$

，而双曲线

$xy=\frac{1}{2}$

则是由标准双曲线

$x^2-y^2=1$

通过逆时针旋转得到的。

利用双曲函数叫“双曲函数”的原因解题

介绍反比例函数图象为什么是双曲线，以及双曲线和双曲函数的关系（为什么双曲函数叫“双曲函数”），不仅能够回答我们对数学概念命名的疑惑，有时还能意外地解决一些问题。

比如

计算 $\int\frac{1}{\sqrt{1+y^2}}\text{d}y$

解：原式

$\xlongequal{y=\sinh t}\int\frac{\text{d}(\sinh t)}{\cosh t}=\int\frac{\cosh t}{\cosh t}\text{d}t=t+C=\ln\left(\sqrt{1+y^2}+y\right)+C$

从

$t+C$

到

$\ln\left(\sqrt{1+y^2}+y\right)+C$

，就是直接利用双曲角是

$t=\ln(x+y)$

一步得出的。

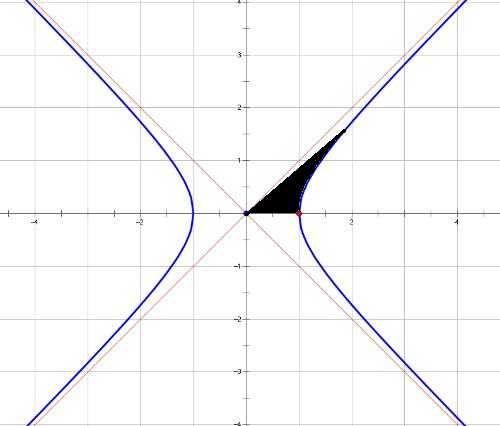
再比如

计算 $\mathop\iint_D x^2y^2\text{d}x\text{d}y$ ，其中 $D$ 是由两条双曲线 $xy=1, xy=2$ 和两条直线 $y=x, y=4x$ 所围成的在第一象限内的闭区域。（同济版《高等数学》第七版习题 10-2 第 19(2)题）

这道题就完全可以使用双曲函数来算，首先对坐标系进行变换

$\begin{cases}x=\dfrac{\sqrt{2}}{2}(u-v)\\y=\dfrac{\sqrt{2}}{2}(u+v)\end{cases}$

，这样，双曲线的实轴就贴在

$u$

轴上了，这时

原式

$=\mathop\iint_{D_1}\frac{1}{4}\left(u^2-v^2\right)^2\cdot\frac{\partial(x, y)}{\partial(u, v)}\text{d}u\text{d}v=\mathop\iint_{D_1}\frac{1}{4}\left(u^2-v^2\right)^2\text{d}u\text{d}v$

这时候，双曲线

$xy=1, xy=2$

就变成了

$u^2-v^2=2, u^2-v^2=4$

，直线

$y=x, y=4x$

也就变成了

$v=0, v=\frac{3}{5}u$

，因为图形是由双曲线和通过原点的直线围成的，因而我们可以搞出一个“双曲极坐标系”，这样问题就会大大简化。

设

$\begin{cases}u=r\cosh\theta\\v=r\sinh\theta\end{cases}$

，则

$\begin{cases}r=\sqrt{u^2-v^2}\\\theta=\ln\dfrac{u+v}{\sqrt{u^2-v^2}}\end{cases}$

这样双曲线

$u^2-v^2=2, u^2-v^2=4$

就变成了

$r=\sqrt{2}, r=2$

，

直线

$v=0, v=\frac{3}{5}u$

也就变成了

$\theta=0, \theta=\ln 2$

，

原式

$=\mathop\iint_{D_1}\frac{1}{4}\left(u^2-v^2\right)^2\text{d}u\text{d}v =\mathop\iint_{D_2}\frac{1}{4}r^4\cdot\frac{\partial(u, v)}{\partial(r, \theta)}\text{d}r\text{d}\theta$

$=\mathop\iint_{D_2}\frac{1}{4}r^5\text{d}r\text{d}\theta=\int_\sqrt{2}^2\frac{1}{4}r^5\text{d}r\cdot\int_0^{\ln2}\text{d}\theta=\frac{7}{3}\ln2$

反双曲函数

接下来推导一下反双曲函数，有了

$x^2-y^2=1$

和

$t=\ln(x+y)$

，这个事情就变得更简单了（根据上文，点

$(x, y)$

在双曲线的右支上，所以有

$x>0, -x<y<x$

，画一下双曲线看看右支和双曲线渐近线的关系就可以搞清楚这两个不等关系，所以

$x+y>0, x-y>0$

）。

反双曲正弦：

$t=\text{arsinh }y=\ln(x+y)=\ln\left(\sqrt{y^2+1}+y\right)$

反双曲余弦：

$t=\text{arcosh }x=\ln(x+y)=\ln\left(x\pm\sqrt{x^2-1}\right)$

，因为双曲余弦函数是偶函数，所以需要确定值域范围，通常选择非负实数作为值域，此时

$y>0$

，故

$\text{arcosh }x=\ln\left(x+\sqrt{x^2-1}\right)$

反双曲正切：

$t=\text{artanh }\frac{y}{x}=\ln(x+y)=\ln\sqrt{\frac{(x+y)^2}{1}}=\frac{1}{2}\ln\frac{(x+y)^2}{x^2-y^2}$

$=\frac{1}{2}\ln\frac{(x+y)^2}{(x+y)(x-y)}=\frac{1}{2}\ln\frac{x+y}{x-y}=\frac{1}{2}\ln\frac{1+\dfrac{y}{x}}{1-\dfrac{y}{x}}$

反双曲余切：

$t=\text{arcoth }\frac{x}{y}=\text{artanh}\left(\frac{x}{y}\right)^{-1}=\frac{1}{2}\ln\frac{1+\dfrac{y}{x}}{1-\dfrac{y}{x}}=\frac{1}{2}\ln\frac{\dfrac{x}{y}\left(1+\dfrac{y}{x}\right)}{\dfrac{x}{y}\left(1-\dfrac{y}{x}\right)}$

$=\frac{1}{2}\ln\frac{\dfrac{x}{y}+1}{\dfrac{x}{y}-1}$

反双曲正割：

$t=\text{arsech }\frac{1}{x}=\text{arcosh}\left(\frac{1}{x}\right)^{-1}=\ln\left(\left(\frac{1}{x}\right)^{-1}+\sqrt{\left(\frac{1}{x}\right)^{-2}-1}\right)$

反双曲余割：

$t=\text{arcsch }\frac{1}{y}=\text{arsinh}\left(\frac{1}{y}\right)^{-1}=\ln\left(\sqrt{\left(\frac{1}{y}\right)^{-2}+1}+\left(\frac{1}{y}\right)^{-1}\right)$

汇总一下，设自变量为

$z$

，则

$\text{arsinh }z=\ln\left(\sqrt{z^2+1}+z\right)\\ \text{arcosh }z=\ln\left(z+\sqrt{z^2-1}\right)\\ \text{artanh }z=\frac{1}{2}\ln\frac{1+z}{1-z}\\ \text{arcoth }z=\frac{1}{2}\ln\frac{z+1}{z-1}\\ \text{arsech }z=\ln\left(\frac{1}{z}+\sqrt{\frac{1}{z^2}-1}\right)\\ \text{arcsch }z=\ln\left(\sqrt{\frac{1}{z^2}+1}+\frac{1}{z}\right)$

其它关于双曲函数的知识，可参考：

王希：可能是最好的讲解双曲函数的文章

最后， @知识库。

查看知乎讨论