这个问题叫做“形态发生学”,是图灵的研究成果之一。
一、从扩散现象说起
你有没有试过……把一滴墨水滴在宣纸上?你看到了什么?
以墨水为中心,一团黑色慢慢晕开,变成了一大片浓淡不一的、不太规则的圆形图案,对吧?
那么,为什么会产生这样的图案呢?
我们知道,宣纸吸水性很强;里面纤维纵横,但大致可认为是各向同性的。
滴墨的地方墨水浓度高,周围没有墨水;那么墨水就会从浓度高的地方往浓度低的方向扩散,对吧。
如果以墨水所在位置为原点,那么我们是不是马上就可以知道,距离原点距离为 r 的点,它大致会在相同的时间 t 被晕染上墨水,对吧?
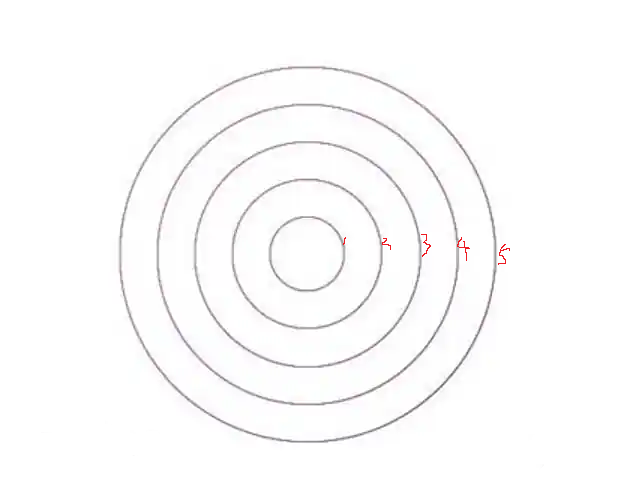
如上图,墨水大概会在 t1 的时刻、近乎同时的铺满圆 r1;然后在 t2 时刻、近乎同时的铺满圆 r2……依次类推,直到铺满 r5,对吧。
现在,让我们玩的花一些。
假如我们事先在如上位置滴上一滴烧熔的蜡油,然后再在圆中心滴上墨水,现在墨水会如何扩散?
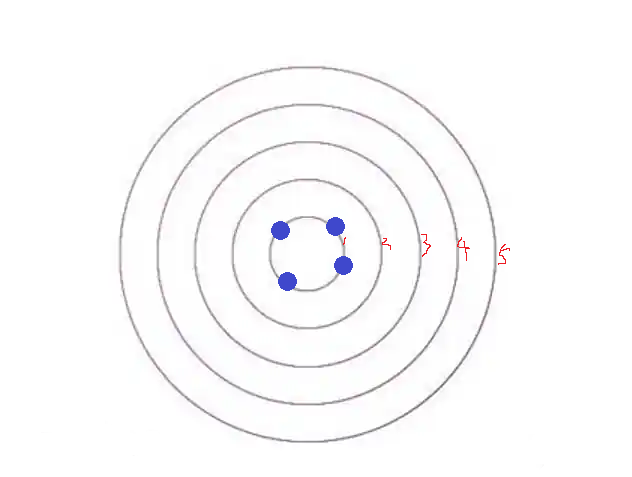
好好想一想。
应该……类似这样,对吧?
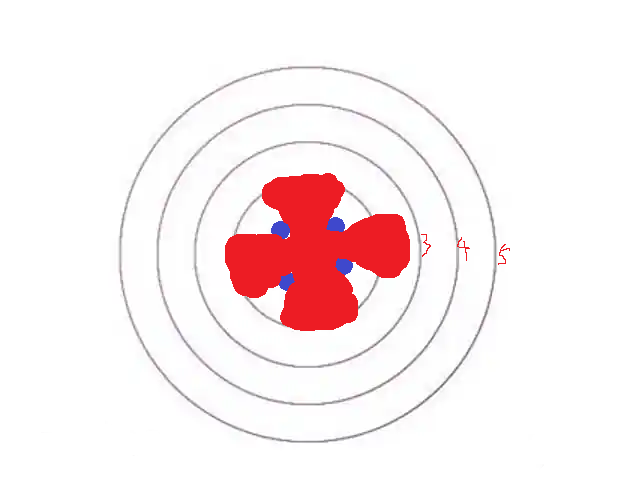
那么,如何用数学语言来描述这种扩散现象呢?
以 r1 圆边缘的每一点为中心,往外均匀扩散——除了蓝色的、被蜡油排斥的区域——对吧?
蜡油点的太刻意了?
那么,如果我们随机喷溅一些蜡油、再点上墨呢?
墨水的扩散,是否出现了某种“模式”?
那么,更进一步,假如我们拿来扩散的液体不是墨水,而是精心调配的“碘钟”反应液呢?会不会扩散出去同心斑纹?
二、细胞繁殖
很容易想到,细胞繁殖其实也类似扩散过程,对吧?
你看,受精卵一分为二、二分为四、四分为八……这是不是就造成了一个密度梯度?
有了这个梯度,是不是就会驱动细胞往外扩散?
如果细胞很少、没有分化,那么这会形成什么?
一个圆球,对吧?

但如果它比较大、重力起到了关键作用呢?

那么,如果细胞产生了分化呢?一些细胞分裂慢、另一些分裂的快呢?

如果细胞分化需要的能量 / 物质来自根、这些营养物质需要“脉管”运输呢?

你看,这就是对称性的来源。
三、更复杂的形态
现在,让我们回到这幅图:
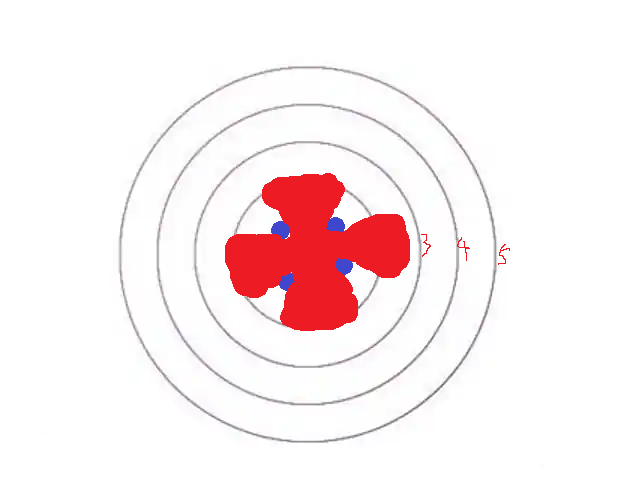
假如这是某种生物发育初期的照片;蓝色是初期分化的某种细胞;那么,继续发育下去,它会长成什么模样?
是不是蓝色也会扩散?而且,一边扩散一边还会被不断分裂的“内部细胞”“推动”着往外移动?
我们是否可以为此写一个“细胞发育动力学方程”,用它来表示这个“生物”的发育过程呢?
当然,这个方程写出来很简单;计算……也不难,就是繁琐,每一个时刻都有不同状态……
不过,好在我们现在有计算机;写一个程序,每个 tick 或每几个 tick,不同的细胞分裂一次或多次,是不是就能完美模拟它的发育了呢?
这正是图灵的发现:各种生物的花纹、形态,其实都可以归结为这样一组“动力学方程”相互作用、相互干扰的结果。这叫图灵斑:

几种图灵斑(Turing Patterns)的简单 matlab 演示(BZ 反应、Gray-Scott 模型、LE 模型)
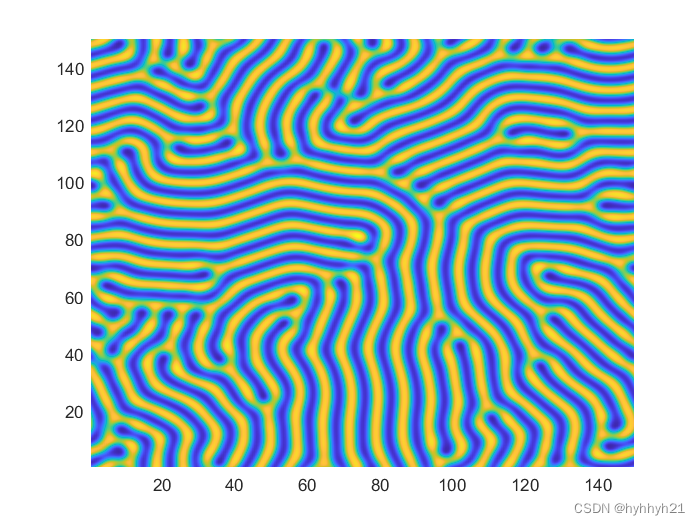
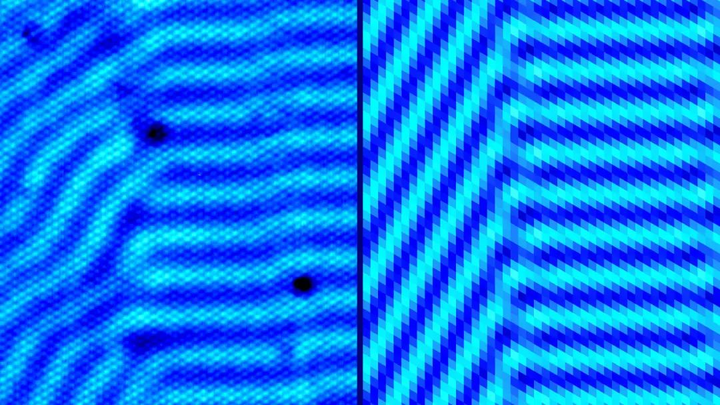
图灵斑广泛存在于各种生物、非生物中间。
事实上,它的形成通常需要一个激活子(促进自身产生)和一个抑制子(抑制激活子产生),且抑制子扩散得比激活子更快。这种"短程激活、长程抑制"的机制才能产生稳定的周期性图案。
四、关于题主问题的回答
为什么自然界会存在对称、黄金比例、斐波那契数列等等各种形态?
——事实上,题主完全可以更大胆一下:为什么对称、黄金比例、斐波那契数列等等规律会如此普遍的出现在自然界,无论生物还是非生物都可能体现?
答案很简单:因为它们的生长 / 扩散 / 结晶等等动力学过程,其核心规则总是被若干“简单”的动力学方程决定的。
哦,当然,这个说法太文绉绉了,也不由自主的混淆了因果关系——它们的生长、扩散、结晶等等过程,遵循的物理规律 / 数学规律是简洁的、可以被动力学方程描述的!
举例来说,植物侧枝排布,它是如何表现出规律性的呢?
让我们仍然回到这幅图:
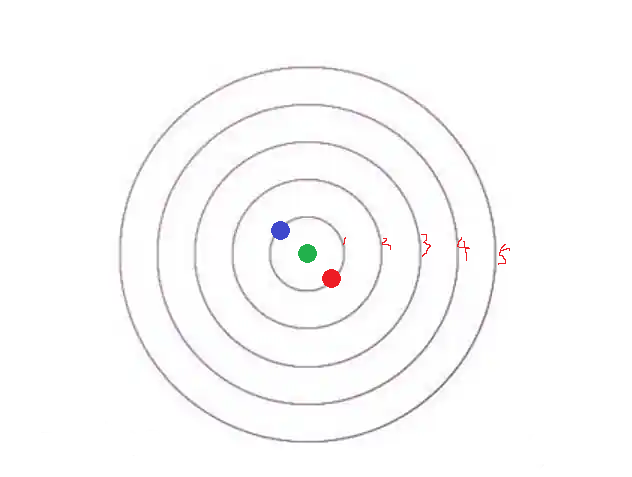
绿色点表示最初的“受精细胞”,也就是顶芽;顶芽会分泌“生长激素”——已知低浓度的生长激素会促进细胞发育 / 分裂,高浓度的“生长激素”反而会抑制分裂。
那么,顶芽发育初期,或许存在一个机制,它可以抑制其他“顶芽”形成;这就使的植物“一枝独秀”,一个劲儿的往上长,尽快冒头,尽快超过其它杂草、获得更多阳光。
而当它生长到一定程度时,“抑制顶芽产生”的酶扩散到全身之后,就不够抑制新的顶芽产生了——它甚至可能打开某个基因、转而分泌促进顶芽产生的酶。于是红色顶芽产生。
为什么顶芽只能在顶部产生呢?因为那里的细胞最“原始”、是未分化的“干细胞”;而下方老枝已经分化了,自然无法产生新的顶芽。
红色顶芽产生后,也会分泌抑制顶芽产生的酶;那么相对来说,蓝色位置就是酶浓度最低、同时又有分化能力的地方,对吧?
于是,在对称的位置,另一个顶芽产生了。
但,绿色顶芽仍然会大量分泌生长激素,这就使得红色 / 蓝色顶芽虽然产生了、但却无法发育;只有绿色顶芽周围的细胞仍然在快速分裂——导管束等等的分裂增长就使得植物迅速长高,绿色顶芽和红 / 蓝色顶芽分离。
等三者分离的足够远、绿色顶芽不再能抑制它们生长时,侧枝就萌发了。
同样的,蓝 / 绿色顶芽发育的侧枝也会经历同样的故事——同时,来自侧枝的生长激素也会运抵绿色顶芽处,它就抑制了原本发育出红绿色顶芽的位置再次分化出顶芽。
如此一来,新的顶芽是不是就只能在“生长浓度相对最低”的紫、橙二处分化出来了?
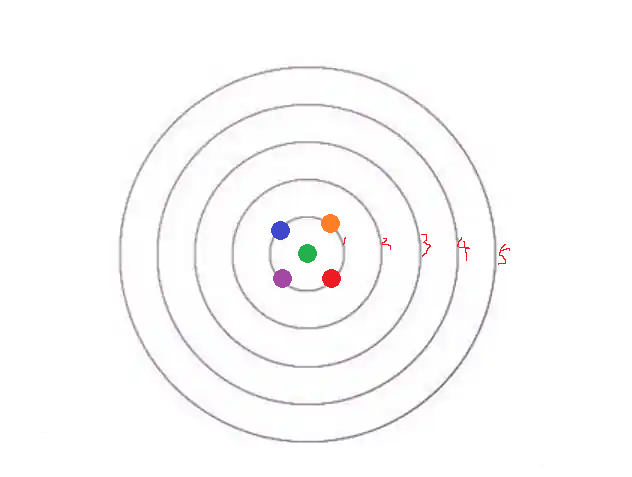
然后,主枝继续长高;蓝 / 红色顶芽对绿色顶芽附近的影响越发淡化,但紫 / 橙色方向有了较强的抑制——下一对顶芽是不是就又回到蓝 / 红色位置了?
你看,这个机制,是不是就恰好保证了“植物侧枝 / 叶片生长错落有致”?

当然,这只是对植物侧枝发育这样一个简单情况的、最理想化的猜测而已;现实中,植物发育要更加复杂、同时还会受到环境的各种影响(趋光性、光照导致的激素分泌分布改变、内外圈生长率的差异,等等),最终的形态自然是……大自然不会有两片完全相同的叶子。
至于动物,尤其哺乳动物这样复杂生命的生长发育过程,它就更复杂、更精密了。
这也是为什么“低等动物”如蚯蚓、涡虫等等有着极强的“再生能力”,而我们却无法再生肢体的根本原因:不是我们“失去了再生能力”,而是“我们身体的发育过程太复杂、太精密”——于是,当肢体缺失后,想要重新发育出一个来……此时动力学函数的初始值(微环境)已经大相径庭,“发育”只会浪费能量、造成畸形,反而大幅削弱我们的生存能力。
事实上,哪怕是树,它受伤后再生,也往往会形成这样的畸形组织:

咳咳,跑题了。
总之,为什么生物会呈现对称美、数学美,是因为它的发育遵循“细胞动力学”约束;而动力学方程会自然产生极具对称性、规律性的图案。
至于黄金分割、斐波那契数列等等,则和“空间排布”有关。这里有精彩的论述,我就不饶舌了:
总之,当你知道它们的发生机制、生长方式时,这些都是自然而然的——或者说,可以基于“形态发生学”推导出来的。
研究“动力学方程”产生的各种图案 / 形态是一个方兴未艾的新领域;师承图灵的计算机科学本身又给这个领域插上了翅膀。这就是分形:


