Question

查看知乎讨论

Answer 1

酱紫君，QQ群1014125

来个猎奇的,五次方程的超几何函数解:

-----------------------------------------------------------------------------------------------

首先,我们有个系数都是有理数的五次方程 Eqa

$0 = Eqa = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}$

-----------------------------------------------------------------------------------------------

不管怎么说我们都可以把五次项的系数变成 1 对吧?

$0 = Eqb = {b_0} + {b_1}x + {b_2}{x^2} + {b_3}{x^3} + {b_4}{x^4} + {x^5}$

其中

${b_i} = {a_i}/{a_5},i \in \{ 0,1,2,3,4\}$

-----------------------------------------------------------------------------------------------

想想三次方程怎么解的我们可以消掉四次项

令

$x \to x - \frac{{{b_4}}}{5}$

,我们可以得到如下形式的方程

$0 = Eqc = {c_0} + {c_1}x + {c_2}{x^2} + {c_3}{x^3} + {x^5}$

然后对比下系数我们能得到

${c_3} = {b_3} - \frac{{2{b_4}^2}}{5}$

${c_2} = {b_2} - \frac{{3{b_3}{b_4}}}{5} + \frac{{4{b_4}^3}}{{25}}$

${c_1} = {b_1} - \frac{1}{{125}}{b_4}\left( {50{b_2} + 3{b_4}\left( { - 5{b_3} + {b_4}^2} \right)} \right)$

${c_0} = {b_0} + \frac{{{b_4}\left( { - 625{b_1} + {b_4}\left( {125{b_2} - 25{b_3}{b_4} + 4{b_4}^3} \right)} \right)}}{{3125}}$

接下来的内容会越来越暴力,直至少儿不宜....现在按返回还来得及!!!!

----------------------------------------------------------------------------------------------------

刚刚那个是一次代换对吧,然后我们可以用二次代换

$y = \frac{{2{c_3}}}{5} + \frac{{ - 15{c_2} + \sqrt 5 \sqrt {45{c_2}^2 - 40{c_1}{c_3} + 12{c_3}^3} }}{{10{c_3}}}x + {x^2}$

把式子变成等价的消去三次项的形式 Eqd

$0 = Eqd = {d_0} + {d_1}y + {d_2}{y^2} + {y^5}$

其中...系数的话...真要比对还是可以比对出来的

----------------------------------------------------------------------------------------------------

一次二次然后接下来四次代换

$z = \varepsilon + \delta y + \gamma {y^2} + \beta {y^3} + \alpha {y^4}$

来变成

$0 = Eqe = {e_0} + {e_1}z + {z^5}$

的形式

其中

$\alpha = - 15{d_2}$

$\beta = - \frac{{15}}{2}{d_2}\left( {\frac{{400{d_0}d_1^2 - 375d_0^2{d_2} - 27{d_1}d_2^3}}{{ - 160d_1^3 + 300{d_0}{d_1}{d_2} + 27d_2^4}} + 3\sqrt 5 \sqrt {\frac{{d_2^2\left( {3125d_0^4 + 256d_1^5 + 2250d_0^2{d_1}d_2^2 - 27d_1^2d_2^4 + 4{d_0}{d_2}\left( { - 400d_1^3 + 27d_2^4} \right)} \right)}}{{{{\left( { - 160d_1^3 + 300{d_0}{d_1}{d_2} + 27d_2^4} \right)}^2}}}} } \right)$

$\gamma = 5(5{d_0} + 4{d_1}(\frac{{400{d_0}d_1^2 - 375d_0^2{d_2} - 27{d_1}d_2^3}}{{ - 320d_1^3 + 600{d_0}{d_1}{d_2} + 54d_2^4}} + \frac{3}{2}\sqrt 5 \sqrt {\frac{{d_2^2\left( {3125d_0^4 + 256d_1^5 + 2250d_0^2{d_1}d_2^2 - 27d_1^2d_2^4 + 4{d_0}{d_2}\left( { - 400d_1^3 + 27d_2^4} \right)} \right)}}{{{{\left( { - 160d_1^3 + 300{d_0}{d_1}{d_2} + 27d_2^4} \right)}^2}}}}$

$\varepsilon =3 d_2 \left(-4 d_1-3 d_2 \left(\frac{3}{2} \sqrt{5} \sqrt{\frac{d_2^2 \left(256 d_1^5-27 d_2^4 d_1^2+2250 d_0^2 d_2^2 d_1+3125 d_0^4+4 d_0 d_2 \left(27 d_2^4-400 d_1^3\right)\right)}{\left(27 d_2^4+300 d_0 d_1 d_2-160 d_1^3\right){}^2}}+\frac{-27 d_1 d_2^3-375 d_0^2 d_2+400 d_0 d_1^2}{54 d_2^4+600 d_0 d_1 d_2-320 d_1^3}\right)\right)$

特别感谢 Mathematica 的一键 Latex....不然我已经输公式而死了...

然后要用 di 表示 ei 也不是不可以,也就这个样子罢了:

注意滑动条和缩放比例....

----------------------------------------------------------------------------------------------------

接下来还要做代换

$x \to \frac{x}{{{{\left( { - {e_1}} \right)}^{1/4}}}}$

变成

$0 = Eqg = {g_0} - z + {z^5}$

的形式,

其中

${g_0} = \frac{{{e_0}}}{{{{\left( { - {e_1}} \right)}^{5/4}}}}$

,嗯,这一步挺简洁的

然后想想 e0 和 e1 的表达式有多长,然后想想还要一步步回代到 ai,然后想想全部展开.....

------------------------------------------------------------------------------------------------------

当然你说这个死样几百年前的古代数学家怎么可能搞得出来.....

我说了这个是猎奇向答案,所以这个是用牛顿恒等式(Newton's identities)算出来的,因为这个编程实现比较容易.

实际上我们有一种叫做结式(Resultant)的方法稍微容易的计算出表达式....

SE 上有这个过程,有兴趣可以看看:

field theory

,还附带椭圆函数解法...不过没有超几何函数解法优雅...

但是不管怎么说 g0 还是可以用根式表达出来的.

${x^5} - x + t = 0$

这个形式被称为布灵·杰拉德正规式

------------------------------------------------------------------------------------------------------

解这个方程就真的是暴力美学了

考虑三项式方程

${x^N} - x + t = 0$

令

$x = {\zeta ^{ - \frac{1}{{N - 1}}}}$

,所以

$\phi \left( \zeta \right) = {\zeta ^{\frac{N}{{N - 1}}}}$

,因此有

$\zeta = {e^{2\pi i}} + t\phi \left( \zeta \right)$

两边做拉格朗日展开

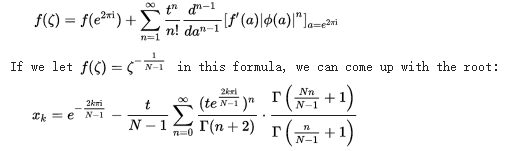
然后我们来把上面一坨写成超几何函数

有点看不清....我们来写成 Mathematica 代码:

x[m_,n_Integer,t_]:=
Sum[-((t^k*E^((2*Pi*I*(k-1)*m)/n)*Pochhammer[(k-1)/n+1,k-1]*
HypergeometricPFQ[Range[n]/(n+1)+(k-1)/n,
Delete[Range[k+1,k+n],n-k]/n,
(n+1)*(((n+1)*t)/n)^n])/(n*k!)),{k,0,n-1}]
TraditionalForm[x[1,4,\[Lambda]]]

代码输出了以下答案

$\begin{gathered} {x} = - \frac{1}{4}\lambda {{\mkern 1mu} _4}{F_3}\left( {\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5};\frac{1}{2},\frac{3}{4},\frac{5}{4};\frac{{3125{\lambda ^4}}}{{256}}} \right) \hfill \\ - i{{\mkern 1mu} _4}{F_3}\left( { - \frac{1}{{20}},\frac{3}{{20}},\frac{7}{{20}},\frac{{11}}{{20}};\frac{1}{4},\frac{1}{2},\frac{3}{4};\frac{{3125{\lambda ^4}}}{{256}}} \right) \hfill \\ + \frac{5}{{32}}{\lambda ^3}{{\mkern 1mu} _4}{F_3}\left( {\frac{7}{{10}},\frac{9}{{10}},\frac{{11}}{{10}},\frac{{13}}{{10}};\frac{5}{4},\frac{3}{2},\frac{7}{4};\frac{{3125{\lambda ^4}}}{{256}}} \right) \hfill \\ - \frac{5}{{32}}i{\lambda ^2}{{\mkern 1mu} _4}{F_3}\left( {\frac{9}{{20}},\frac{{13}}{{20}},\frac{{17}}{{20}},\frac{{21}}{{20}};\frac{3}{4},\frac{5}{4},\frac{3}{2};\frac{{3125{\lambda ^4}}}{{256}}} \right) \hfill \\ \end{gathered}$

唔....也许你对这个结果的优雅性没有感觉...

这样说吧,四次方程的根式解输入知乎是这个样子的

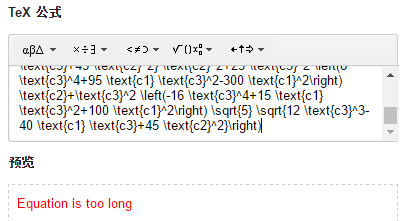
但是用超几何函数记法可以优雅简洁的写成

$x = - t{_3}{F_2}\left( {\frac{1}{4},\frac{1}{2},\frac{3}{4};\frac{2}{3},\frac{4}{3}; - \frac{1}{{27}}\left( {256{t^3}} \right)} \right)$

------------------------------------------------------------------------------------------------------

嗯,所以结论就是绝大多数五次方程没有根式解,绝大多数有根式解手算化不成布林 - 杰拉德形式,绝大多数可以化简的写成超几何函数形式也长的没法手算....所以

天灭解析式,数值保平安

数学中有哪些明明是暴力破解还给人美感的证明？