我最近写了一篇有关量子人工智能的论文,同时在知乎专利上写了对此工作的介绍,某种程度上可以回答这个问题。
去年,我们发现基于离散量子时间晶体量子模拟线路可以开发高效的量子变分算法,避免贫瘠高原现象。这个发现让我特别兴奋,特意写了一篇科普《从时间晶体到变分量子算法》介绍。虽然我们从离散时间晶体量子模拟线路出发进行研究,但最终结论是多体局域化可以辅助变分量子算法(VQE)避免梯度下降问题,并没有看到多体局域化中的离散时间晶体对 VQE 效率有促进作用。量子时间晶体是不是真能提升人工智能的效能,仍有待验证。由此我们注意到量子时间晶体线路在人工智能中的巨大潜力,开展了系统深入的研究。
2024 年诺贝尔物理奖颁给了人工智能的两位鼻祖:Hopfield 和 Hinton,让预测诺贝尔奖的人都大跌眼镜,对我们这种刚进入机器学习领域开展研究的人来说,却是很大的激励。如果仔细考察两位获奖人的成就,拿到诺贝尔物理奖也不无道理。Hopfield 是典型的物理学者,他提出的 Hopfield 网络,源自统计物理中的 Ising 模型;而 Hinton 是一位人工智能学家,他在 Hopfield 网络的基础上提出玻尔兹曼机,作为神经网络中的标准模型,也与经典统计物理密切相关。作为一名人工智能学者,Hinton 一直坚守机器学习研究领域。直到 2010 年代,他与他的学生基于深度学习在图像识别领域产生突破,从而开启今日的人工智能革命。
我猜测,把经典机器学习算法推广到量子机器学习,第一步就得把神经网络的底层逻辑从经典统计物理推广到量子统计和量子多体物理,设计相应的量子神经网络与量子线路,让量子计算机能发挥全部能力。这种推广显然极为困难。首先遇到的问题还是贫瘠高原。量子神经网络的表达能力随着量子比特数指数增长,因此其希尔伯特空间维度也是指数大的。如果对量子线路进行调参,贫瘠高原问题很难避免。其次,是调参时反向梯度传播问题。在经典机器学习中,神经网络的反向梯度传播,可以通过求导加上链式法则快速计算。而对量子神经网络调参时,并不存在反向梯度传播链式法则。只能用类似数值差分的方法对测量结果求差值,计算出梯度。
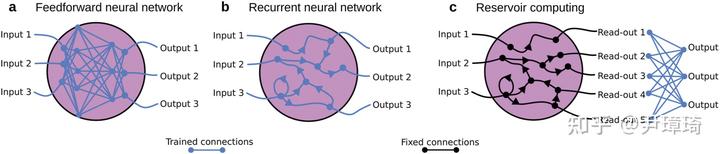
既然量子机器学习中线路调参有这么多问题,可不可以不调参呢?还真是有。如上图所示,在典型的机器学习中,包括前馈神经网络,它具有单向非循环且可训练前馈连接;循环神经网络,它具有可训练的反馈和循环连接;以及储备池计算,它无需训练,只需对输入和输出结果进行线性回归拟合即可。储备池计算,基于稀疏且巨大的变换矩阵,可以代替需要调参经典神经元网络。储备池计算最神奇的地方在于,中间层稀疏矩阵只需在初始时随机生成,计算过程中无需进行调整训练。受到储备池计算的启发,人们提出了量子储备池计算。量子储备池计算,继承了经典储备池计算无需训练的优势,同时由于量子动力学系统天然的非线性,以及量子多体系统维度随着量子比特数指数递增的特性,它相比经典储备池计算更有潜力。在量子储备池计算框架下,并不需要对参数进行精准调控,因此尤其适用于目前中尺度含噪声量子计算系统。
2024 年 7 月,美国 QuEra 公司、哈佛大学和科罗拉多大学联合团队在预印本网站上贴出了他们基于量子储备池计算的实验论文,报道了他们基于中性原子阵列量子模拟器实现的量子储备池计算实验,其中最多使用了超过 100 个中性原子。他们的实验发现,随着原子数的增加,识别图像的成功率随之上升。对于手写字体数据集 MNIST,10 分类任务准确率随着原子数增加而增大,实验中最多用了 100 个原子,识别准确率达到 60% 左右。但这个实验中仍存在很多噪声,导致实验中的识别成功率始终比无噪声理论模拟结果要低 10%。尽管量子储备池计算无需对参数精准控制,但噪声仍是其迈向实际应用的重要障碍。
既然在量子线路中,噪声不可避免,有没有什么办法可以消除其效果呢?2022 年,美国谷歌公司利用量子计算机模拟实现了多体局域化离散量子时间晶体,不仅对初态信息具有拓扑保护特性,同时还有足够的非线性与记忆效应。由此我们猜测,利用它来做量子储备池计算,不仅可以抵抗噪声影响,还能高效地完成机器学习任务。于是我们基于离散量子时间晶体,发展了可以在通用量子计算机上运行的量子储备池计算算法。为验证其对噪声的稳定性,我们模拟了含噪声的量子时间晶体储备池算法,并用于 MNIST 的手写字体 10 分类任务。如下图所示,数值模拟清晰表明,在目前保真度 99% 左右的量子门参数下,分类准确率相比无噪声系统的准确率几乎没有下降。随着量子比特数从 4 增加到 18,识别成功率一直在上升,且与 4 层的全连接神经网络的识别效果基本上一致。最高识别成功率在 90% 附近。
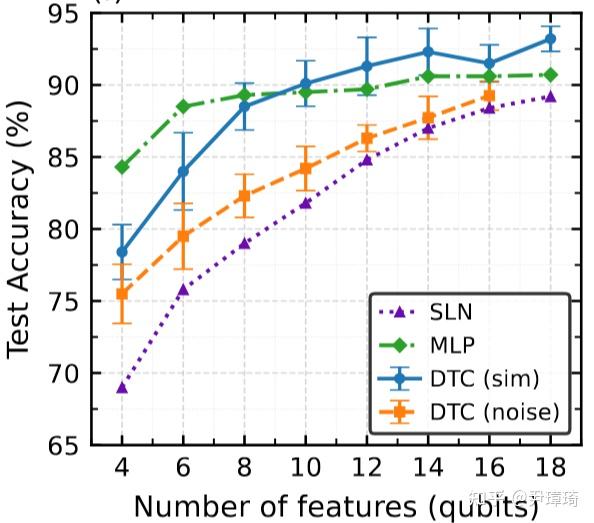
为研究不同量子多体相与储备池计算效果之间的关系,我们还模拟了此模型热化区域和多体局域化顺磁区域中量子储备池计算的效果,发现热化区域中识别准确率大幅度下降。考虑到噪声影响后,热化区域识别准确率会进一步下降到 60% 多,而多体局域化区域的准确率只有 3% 的下降。随着量子比特数增加,含噪声的模拟结果与无噪声的识别准确率的差别还在进一步缩小,这意味着多体局域化拓扑保护效应随量子比特数增加更为显著了。此外,从模拟数据中可以看到,离散时间晶体区相比非时间晶体的多体局域化区,识别准确率还有几个百分点的优势。
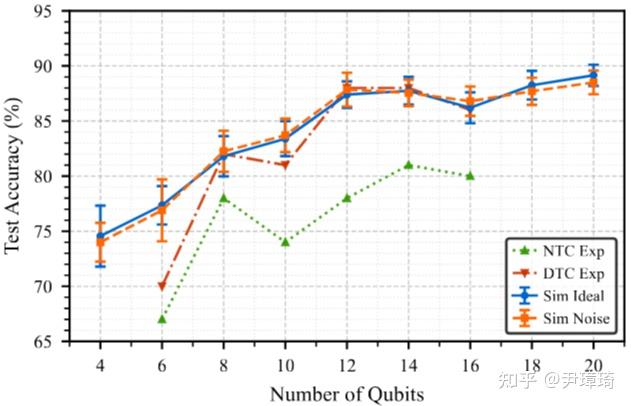
在此基础上,我们与北京量子院合作,利用其量子云实验平台验证了此算法。量子云平台中单量子比特量子门保真度接近 99.9%,双量子比特量子门保真度中位数 98%,实验中用到的双量子门不超过 100 个。对通常量子算法来说,量子门累积错误已经使得量子相干性完全丢失,导致算法失效。如上图所示,在我们的实验中,MNIST 数据集 10 分类识别准确率几乎不受量子门错误的影响。随着量子比特数增加,此算法能近乎完全地消除噪声效果:14 个量子比特时,识别成功率提升到 88%,与无噪声的模拟结果近乎相同。实验同时证明离散时间晶体相变区用于图像识别是最优的,与数值模拟结果一致。需要指出的是,由于量子云平台稳定性和机时限制,我们只使用了 MNIST 数据集中的 500 个进行训练,100 个进行测试。如果能把 MNIST 中六万多个数据全部用起来,识别准确率可以进一步提升到 97% 以上,接近目前机器学习最高的准确率。
总结一下,我们通过模拟和实验两方面确认,多体局域化离散时间晶体对量子储备池计算的拓扑保护,随量子比特数增加越来越好,在量子云平台实验中增加到 14 个量子比特时达到最优。如果能提升量子门保真度,那么最优量子比特数还会进一步提升,从而增加算法的识别准确率。本工作可能是首次在实验上演示了量子多体拓扑保护效应可用于消除量子机器学习中噪声的影响。在拓扑量子计算实现之前,我们先实现了“拓扑保护下的量子机器学习”。
2012 年,我们出于纯粹学术好奇心开始了对时间晶体的研究,并介绍了完全是幻想的时间晶体中的计算机,今天被我们自己初步实现,科研的魅力就在于此!至此本工作介绍完毕,而我们结合量子时间晶体对量子人工智能开展的研究才刚起步!
相关论文:Robust and Efficient Quantum Reservoir Computing with Discrete Time Crystal, Da Zhang, Xin Li, Yibin Guo, Haifeng Yu, Yirong Jin, and Zhang-Qi Yin*, arXiv:2508.15230

