作为学生,我想各位读者们应该在读书学习的时候多少经历过“原本嘈杂的教室突然变的鸦雀无声”的现象。对此已有相当多的答主做出了定性的解释:
1.嘈杂的人群说话的空隙偶然重叠会导致音量的突然下降
2.说话的人会为音量的减小感到警觉而放低说话的音量
基于这两点,我们可以为嘈杂的人群做一个简单的建模并数值模拟:
设人群共 N 人
其中
代表编号为 n 的人在 t 时刻发出的声响(类似于分贝,人在正常范围对"声响"的感知是线性的),
则是其听到的声响。 在正常的嘈杂环境下二者的均值为 1。
的第二部分
代表了一小段时间(此处为 0.3s)内环境音量平均大小对其说话声音的影响,采用
而非正比的形式可以使得
与
稳定在不动点 1 附近,在正常情况下不过大或过小,而在发生突变至 0 后能自行脱离零点回复至 1。第三部分
描述了声音的变化对其影响,标红的 m、n 都是可调的参数,n 代表了引起人警觉的中心阈值,而 2/m 代表这一“警觉”过渡的“宽度”。当声音在半秒内的平均变化率
大于 -n+1/m 时不会造成任何影响,小于 -n+1/m 时人会略微放低声音,而小于 -n-1/m 则会使人彻底闭口不言。
决定了其听到声音的方式,且满足
,视情况可以是随距离衰减,或直接对所有
取平均。
表示他在 t 时刻发言的意愿,g(t)均值为 1,在 0 与 2 间过渡平滑的随机的跳动,此处我令
,其中 A,B…E 都是诸如
的无理数,而 X 则是对每个 n 都不同的随机数。

最末一项
是用来给
的取值兜底的,以免突变过于剧烈使得其直接严格跌落到 0,那就没得玩了,突变后音量还得升回来呢。然而这一项多少有点败笔的意思,总之它“唯像”式的保证了突变以及沉默后音量的回升。
此处我将环境定在一个四十人的教室,考虑到狭小的教室内声音几乎不会衰减,我设
。这一举动将极大的方便了我们的计算,因为我们可以直接将方程改写为
仅用到一个 F,而不是 40 个 F 和 f,这将在后面的数值模拟中帮助我们节省大量的算力。
下面就到了喜闻乐见的写程序(拉屎山)环节:
import math
import numpy as np
#迭代方程
def A(x,y):
k=math.log1p(x)/math.log(2)*0.5*(1+math.tanh(5*(y+1.5)))
return k
#随机函数
def a(t):
c=1+math.tanh(7*(math.sin((math.sqrt(3))*0.7*t)+math.sin((math.sqrt(5))*0.7*t)+0.332*math.sin((math.sqrt(16))*0.7*t)+math.sin((math.sqrt(14))*0.7*t)+1.02*math.sin((math.sqrt(2.5803)*0.7*t))))
return c
def b(t):
d=(a(t)+a(t+10)+a(t+20)+a(t+30)+a(t+40)+a(t+50)+a(t+60)+a(t+70)+a(t+80)+a(t+90))/10
return d
def g(t):
e=(b(t)+b(t+100)+b(t+200)+b(t+300))/4
return e
#时间步长
step=round(0.05,5)
#F 在 t 为 0 前取值的初始化
dict={}#迭代数据暂存
hhh=-1
while hhh<=0:
dict[hhh]=g(hhh)
hhh=round(hhh+step,5)
#记录突变时间
timelist=[]
count=0
realcount=0
#用于绘图记录数据
datadict={}#响度记录
gdata={}#发言意愿记录
#迭代循环
t=0
while t<=360000:
fl=(dict[round(t-0.05,5)]+dict[round(t-0.1,5)]+dict[round(t-0.15,5)]+dict[round(t-0.2,5)]+dict[round(t-0.25,5)]+dict[round(t-0.3,5)])/6
fv=(((dict[round(t-0.05,5)]+dict[round(t-0.1,5)]+dict[round(t-0.15,5)]+dict[round(t-0.2,5)]+dict[round(t-0.25,5)])/5)-((dict[round(t-0.55,5)]+ dict[round(t-0.6,5)]+dict[round(t-0.65,5)]+dict[round(t-0.7,5)]+dict[round(t-0.75,5)])/5))*2
dict[t]=g(t)*A(fl,fv)+0.001*g(t)
datadict[t]=dict[t]
gdata[t]=g(t)
del dict[round(t-0.8,5)]
#以上递推模拟
last=count
if (dict[round(t-0.05,5)]+dict[round(t-0.1,5)]+dict[round(t-0.15,5)]+dict[round(t-0.2,5)]+dict[round(t-0.25,5)])/5>=0.1:
count=0
else:
count=1
if last-count<=-1:
realcount=realcount+1
timelist.append(t)
#以上突变计录
t=round(t+step,5)
#1.75,50h,0 1.6 43 1.5 187(100h410 个) 1.4 约 475 1.3 约 1250 1.2 约 2550 1.1 约 5075 1 约 9200
#以下突变绘制
import matplotlib.pyplot as plt
#绘图循环
n=1
databar={}
kkk=-5
tmd=0.5
while kkk<=5:
databar[kkk]=0
kkk=round(kkk+0.05,5)#平均值初始化
while n<=realcount:
ctime=timelist[(n-1)]
x_values = list(np.arange(ctime-5, ctime+5,0.05))
y_values = [datadict[round(x,5)] for x in x_values]
# g_values= [gdata[round(x,5)] for x in x_values]
x_values=list(np.arange(-5,5,0.05))
if datadict[round(ctime,5)]>=0.06:
tmd=0.7
else:
tmd=0.01
plt.plot(x_values, y_values,alpha=tmd)
# plt.plot(x_values,g_values,"c-")
n=round(n+1,2)
T=-5
while T<=5: #求均值循环
for m in timelist:
databar[T]=databar[T]+(datadict[round(m+T,5)])/realcount
T=round(T+0.05,5)
data_values = [databar[round(x,5)] for x in x_values]
plt.plot(x_values, data_values,"c-")
plt.axis([-5, 5, 0, 2])
plt.show()这里的可视化部分我按需修改了很多,放上来的这一版最终的效果是筛选所有突变,绘制均值并着重标出偏离过大的数据。想要自己跑着玩的话还请自行修改
万事俱备,终于可以开始模拟了。在模拟运行的第 512s,第一个突变出现了!(ohhhhhhhhhhhh)
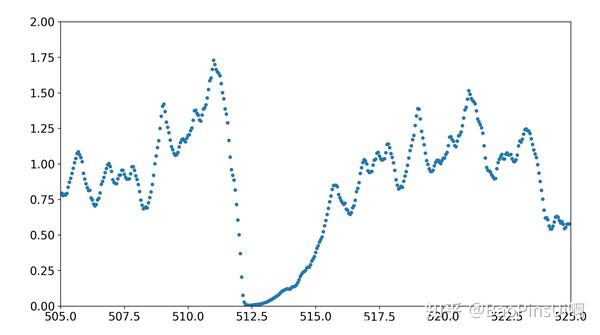
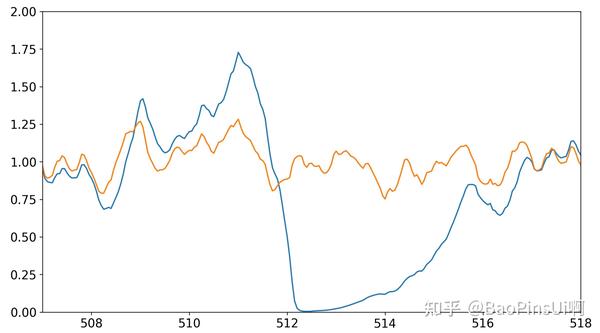
随手写的式子,竟然真的产生了符合预期的输出。让程序继续运行下去,在
的参数下,模拟的 100h 内产生了 410 个突变,这是记录的一些有趣的数据:
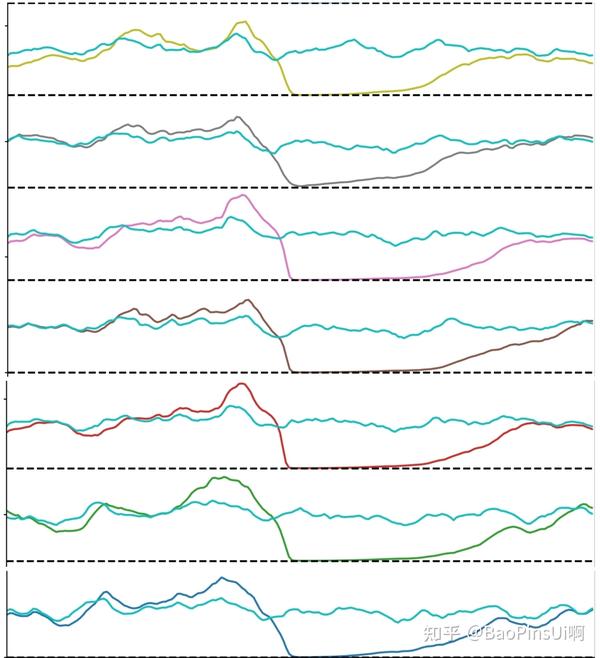
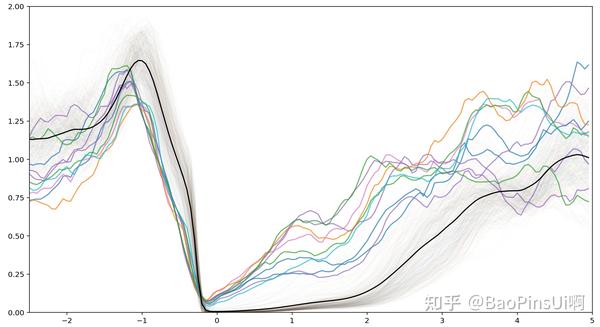
当然这样零散的数据意义不大,接下来我们将这 410 个突变绘制在一起并取平均值:
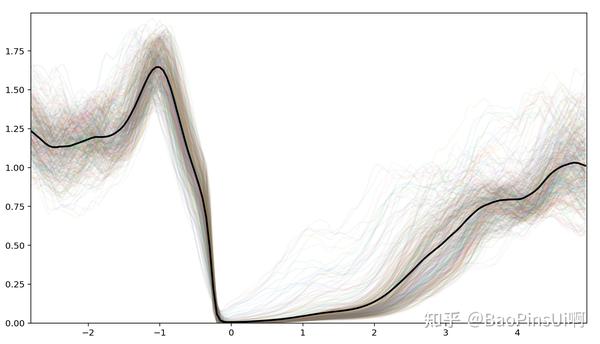
可见在本模型下,“突然安静”现象的典型特征是音量先经历一段时长在 0.4s 左右突增,随后以相反的速度在相同的时间内减小到 0.75 左右,再随后剧烈的衰减至零,保持一至两秒静默后回升。这在现实中均有对应解释,对应着“凑巧出现的波谷前对应的波峰”→“凑巧出现的波谷”→“众人察觉到什么,纷纷闭嘴”→“大家一脸懵逼”→“危机解除,继续聊天”的过程。
值得注意的是图中几条快速回升的数据,它们在下降段同样不如其它数据剧烈,可以将其解释为当下降过程延长时,最后一个人察觉前已经有人意识到“老师没有来,这是场误会”,于是没有出现彻底的静默。
在我出生至现在的七坤年中,我一共经历了三次“突然安静”现象,其中包括一次“不彻底的突变”。虽然能够使得这一场景出现的条件(原则上不能说话的时间,老师不在,大家聊的热火朝天)很少能一起满足,我仍然认为 100h 内出现 410 次突变过高了。我又在不同的参数 n 下进行了时长 50h 的模拟,结果如下:
n=1,184 次 /h
n=1.1,101.5 次 /h
n=1.2,51 次 /h
n=1.3,25 次 /h
n=1.4,9.5 次 /h
n=1.5,4.1 次 /h
n=1.6,0.86 次 /h
n=1.75,0 次
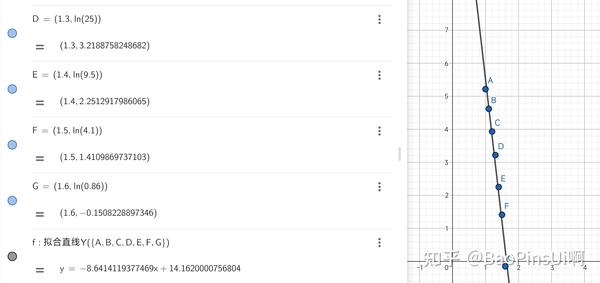
可见每小时安静数大致满足公式
还有不少想说的,以后慢慢写罢
下期预告:
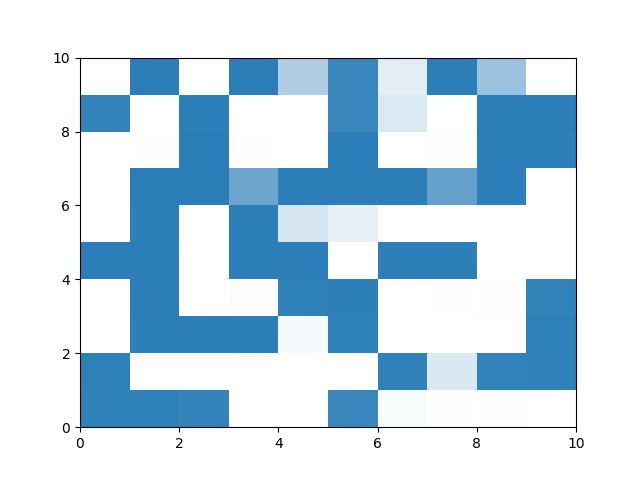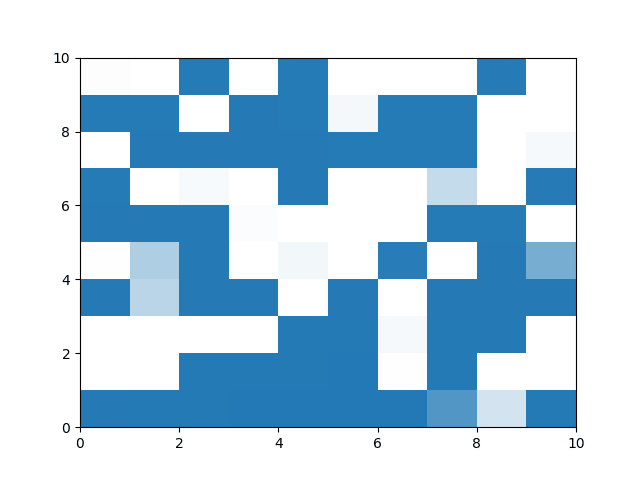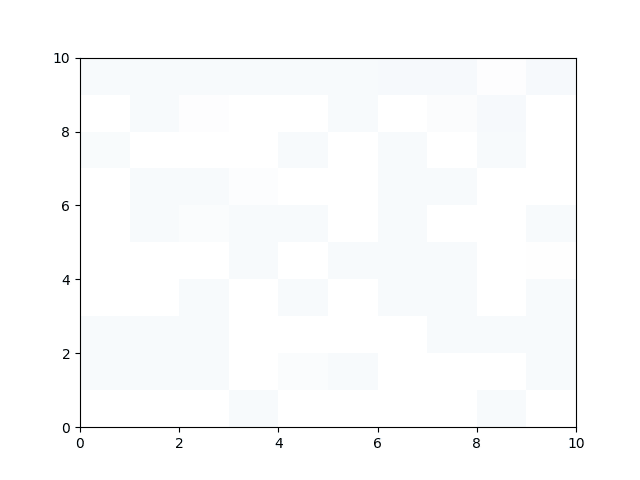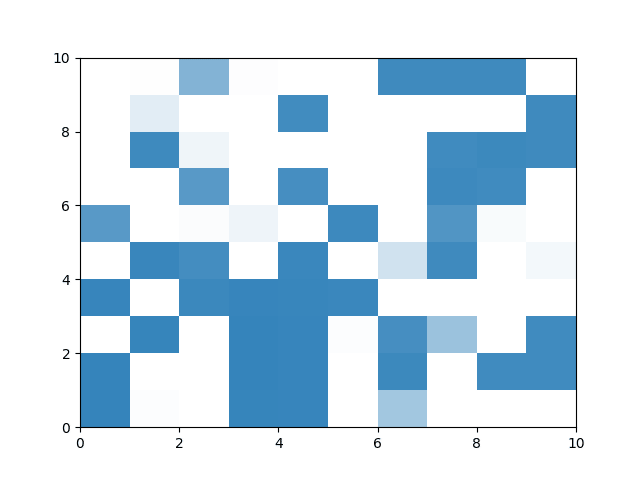
使用 C++ 重制的考虑声音衰减的版本已完成(真正同时在运行 100 个 f),目前正在进行可视化工作,择日发布。
有网友在评论区引用了冯诺依曼的“四参画大象”典故指出了我的模型过于复杂,我在此对我建模的思路进行一下解释
音量由一项音量大小决定和一项音量变化决定:大小那一项一开始是正比,然后为了稳定性取一个凸函数;变化那一项涉及到阈值就自然的用 sign 函数(符号函数),为了这个体系光滑一些就用 tanh 代替符号函数。此外考虑到人感知的是一小段时间声音的均值,所以用了到很多积分号取均值,这让这个式子看起来很冗长。事实上并没有那么不堪,每一项的物理意义还是很清晰的。~( ̄▽ ̄~)~
此外我目前缺少实验数据(网上完全找不到),有记录“突然安静”现象的音视频的网友们可以把文件发送到 [email protected],臣生当陨首死当结草!((((((((((

