我从数学角度给一个标准答案吧:有可能,并且这个可能性还不算太小。换个角度说,猴子赢下职业九段所需要花费的时间,即使只在「科学领域」,都算不上一个特别大的数。
不得不说,日常生活限制了大部分人对数字的想象。但即使是日常生活,都存在一些大得惊人的数,这些数都比猴子赢下职业九段的时间要长得多。
在这里,我们定义一个新的单调递增函数
用于解释科学领域大数的层级。它的范围是
,也就是说,无论多大的数,我都可以映射到一个不超过 3 的数中。在这个映射关系下,「猴子赢下职业九段所需要花费的时间」对应的函数值大约在 1.02~1.04 之间。
第一层 (0,1]:粒子的计数
在这个函数下,生活中的绝大多数数字,对应的值都不超过 1。
比如:
- 普通人每月的收入,对应的值大约是 0.05;
- 世界人口数,对应的值大约是 0.1;
- 世界财富总和,对应的值大约是 0.2;
- 一摩尔物质的量,对应的值大约是 0.3。
事实上,第一层的上限
。这个 10 的 80 次方, 大约就是宇宙中粒子的总数。
也许你想说:怎么一上来就上核武器啊?
别着急,比起我接下来要讲的数,我们才刚刚开始而已。
第二层 (1,2]:粒子的排列
事实上,「计数」是一种很原始的表达方式,即使把宇宙中所有粒子都算上,都可以用简单的科学计数法搞定。
但是一旦涉及到「排列」问题,我们很容易得到一个比第一层大得多的数。其对应的增长速率,也会远高于第一层中所熟悉的数。
魔方大家都熟悉吧?一个最常见的三阶魔方,它的不同状态数就有
个;稍微大一点,五阶魔方,不同状态数达到
个,已经接近宇宙粒子总数的数量级了;而六阶魔方,不同状态数高达
,远超宇宙粒子总数。事实上,如果定义 m(x) 为 x 阶魔方的状态总数,这个函数的增长是非常快的。当 x 不超过 15 时,m(x) 的值如下表所示:
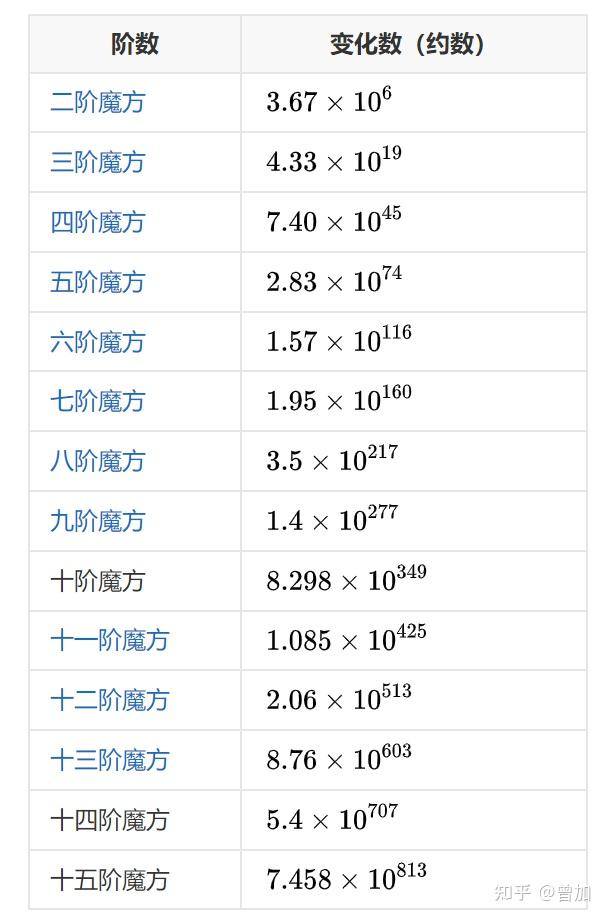
事实上,几乎所有有一定复杂性的智力游戏,其「状态数」和「过程数」都在这一层。
就比如本问题中,猴子和人下棋:
- 棋盘「状态数」上界不超过
(361 个交叉点,每个交叉点有 3 种可能 ),大约是
;
- 棋盘「过程数」上界不超过
(一盘棋一般不超过 300 步),大约是
;
上面只是非常粗略的估计,根据这个估计,「猴子赢下职业九段需要花费的时间」大约会在
这个数量级。这个数对应的函数值是多少呢?大概是在 1.02~1.04 之间。
因为,仅仅对
个粒子进行简单排列,其不同的状态数就有
个,这个数看起来很大,但位数不超过
位,也就是说,这个数至多
,它其实也没多大,但比 10 的 600~800 次方还是要大得多。
事实上,考虑到宇宙的空间很大,远大于粒子本身所占据的空间,因此微观状态数还会更多一些,但也不会超过
因此,作为第二层的上限,
。
顺便提一句,「猴子敲出莎士比亚全集」的时间也在这一层中,并且比「猴子赢下职业九段需要花费的时间」要长得多,但对应的函数值也不过在 1.05~1.08 之间。
第三层 (2,3]:粒子的回归
比「粒子的排列」更大的数是什么呢?是粒子的回归。
展开地说,就是随机运动的微观粒子,是有机会回到原来位置的。如果一个区域中的所有粒子都几乎回到了原来的位置,那么其所需要花费的时间大约就在这一层级。
举个通俗的例子:我们都知道「破镜无法重圆」。但事实上,当我们把破镜的所有碎片收集起来装在一起,只要经历足够多的时间,它是可以重圆的,只是重圆所需要的时间,大概会在第三层,虽然这只是第三层入门。
而这个层级的上限,就是「庞加莱回归时间」:在一个封闭系统中,任何粒子在经过一个漫长的时间之后必然能回到其无限接近其初始位置的位置(但是不能回到原来位置,只能无限接近),这样一个周期就称为一个庞加莱回归。
庞加莱回归时间有多大呢?有些 文章 会对它进行估算,比如算出太阳系的庞加莱回归时间大约是
,如果使用 Linde's stochastic inflationary models 计算整个宇宙的庞加莱回归时间,大约是
。
这才是「科学领域」中最大的有意义的数。比起这个数,猴子赢了职业九段根本不值一提。
--
在科学领域之外……
事实上,在数学领域中,即使是宇宙中最大有意义的数
,依然是小得可怜的数。
在「大数学」(googology )中,人们定义了一套更加严谨的从序数到函数的映射系统,叫
系统(fast-growing hierarchy,简称 FGH),详细的定义可以参见 这里。
「庞加莱回归」时间的表示方式,也不过是最最基础的「幂塔」而已,从数学上来说,它甚至小于
(这不过是 2 层 高德纳箭头 而已!),在 FGH 中,我们也只能给到 2~3 的序数值。
它比起大数学中的入门「葛立恒数(Graham's number)」,还差了 2 层「人到神仙的距离」。
而比起目前人类目前承认的最大数「巨大数庭园数」 (Large Number Garden Number,简称 LNGN),它至少差了至少 10 层「人到神仙的距离」。
但即便是「巨大数庭园数」,依然和「无限」毫无关系。
警告:不要轻易使用 ,这个数比你想象中的要大得多得多!

