居然没人提到爱因斯坦场方程。
物理学家都是懒货,总是喜欢发明一些符号简化方程,让你误以为这很简单
(从此你便走上一条不归之路)

一、爱因斯坦场方程
你以为的爱因斯坦场方程:
(这不是弱爆了嘛?一行就能写完的式子哪里复杂了?)
这是一个二阶张量方程,重复指标代表求和
其中标曲率
是由里奇张量
求迹而得:
而里奇张量
是由黎曼曲率张量
两个指标缩并而得
所以你不得不计算黎曼曲率张量,而黎曼曲率张量是由克里斯托弗联络计算而来:
为了得到黎曼曲率张量你不得不计算克里斯托弗联络系数:
全部代入爱因斯坦场方程中,你便把场方程的左边全部换到度规系数
上了。
二、哑指标展开
这么说,可能还是有点抽象,接下来让我们丧心病狂地把哑指标全部展开
(当然它们的分量并不完全独立,不过我们旨在展示它的复杂程度)
(仅以一个分量为例):
一个克里斯托弗联络
,共
项:
共计
项
一个黎曼曲率张量
,共
项:
按理来说我应该把每个
代进去的,奈何实在敲不动
,见谅见谅
共计
项,代入每个
的
项,对于一个
你需要计算
项,
里奇张量
,共
项:
共计
项,代入每个
的
项,对于一个
你需要计算
项,
标曲率
,共
项:
共计
项,代入每个
的
项,对于标曲率
你需要计算
项。
算到这里,你才仅仅算出来爱因斯坦场方程中的一个方程(这还没考虑物质模型和坐标条件)。
要是想完全计算出爱因斯坦场方程(不包括能量动量张量
),
克里斯托弗联络
共计
个分量,故需要计算
项,
黎曼曲率张量
共计
个分量,故需要计算
项,
里奇张量
共计
个分量,故需要计算
项,
标曲率
,共
项。

三、代入场方程
稍微运算一下,你可以得到下面这玩意儿[1]:
如果你对爱因斯坦求和约定没有什么概念的话,可以把求和号写出来看看,它长下面这样:
如果你还是没对这个方程没概念的话,以第一项求和展开为例,它长下面这样:

你这才展开第一项的求和,后面还有好几项等着你展开。
第二项展开
第三项展开
第四项展开
第五项展开
好家伙,这还成功测试到了知乎公式上限
(这一项总共是
项的和,上面也才仅仅展出了
项)
总之,后面还有第六项,第七项,第八项,第九项,第十项的展开
当你哼哧哼哧全部展开之后,你会发现左边总共有
项!

你要知道爱因斯坦场方程是个二阶张量方程,它足足有
个类似你刚才展出来的方程!!
每一个方程你都可以把左边展成
项,也就意味着你总共需要展成
项!!!

你这才解决场方程左边,还有右边没有算呢!
四、物质模型和坐标条件
然而要完全求解爱因斯坦场方程你还需要以下两个东西:
物质模型,坐标条件
场方程的右侧的能量动量张量
根具体的物质(或者说选取的物质模型)有关,
且爱因斯坦场方程每个方程并不独立(实质上仅有 6 条独立方程),为了完全求解
还需引入谐和坐标条件。
由于爱因斯坦场方程的高度非线性,实际上找到解析解基本是不可能的事情,就算是数值解也颇为复杂。甚至为了求解爱因斯坦场方程还专门发展了一门“数值相对论”的学科。

不过在一些特殊情况下是可以求出解析解的,
比如史瓦西大佬在爱因斯坦发表广义相对论论文后的一个月就得到了真空、球对称(也是稳态)的解(那个时候他甚至还在参加一战的战场上):

五、黑洞、白洞、平行宇宙、爱因斯坦罗森桥、引力波
有了场方程就好玩了,可以讨论一些有意思的事情,
貌似大家刚才看一大坨公式看累了,这里就只放几张示意图好了。
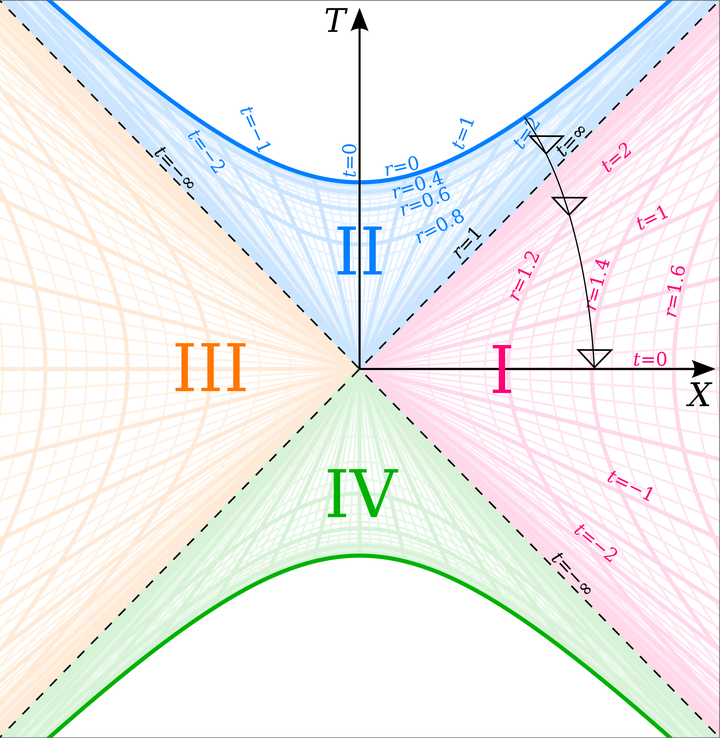
比如大名鼎鼎的 Kruskal–Szekeres 坐标,
I 区是我们的宇宙,II 区是黑洞,III 区或许是平行宇宙?,IV 区是白洞。
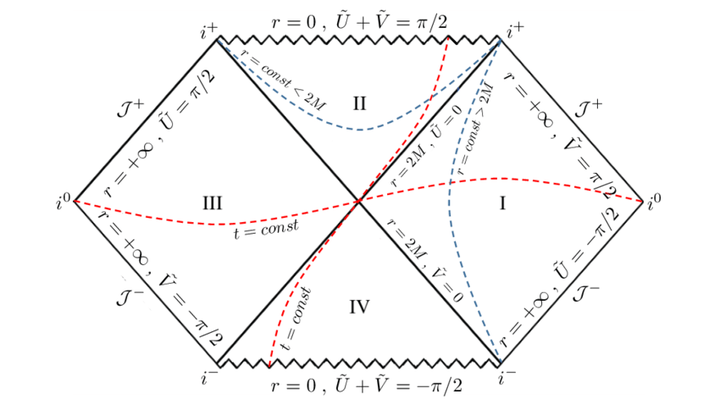
还有或许可以实现时空穿梭的爱因斯坦 - 罗森桥(虫洞)

最后还有我们学院的天琴计划(引力波探测):

当然还有 2019 年 4 月 10 日公布的黑洞照片