几乎所有的高中物理老师都会告诉你:
开普勒经过大量计算,发现行星运行的轨迹是椭圆。
至于他是怎么计算出来的,老师都语焉不详,反正高考也不考,直接略过了。好奇的你可能会去网上找相关的计算过程,发现绝大多数都是用微积分来求证的。可是,当开普勒提出椭圆轨道的第一定律时,发明微积分的牛顿和莱布尼茨两个大冤家还要再等 30 多年才出生呢。
那开普勒是怎么“猜”出轨迹是椭圆的呢?下面会有一个长长的求证过程(难度不超过普通高二物理),如果你下载知乎的初衷不是学习知识,那现在就关掉这个回答吧,那些小姐姐、短视频和键 Z 比这个又长又枯燥的回答有趣多了。
1.知识铺垫:你记忆中的托勒密地心说并不是托勒密地心说
托勒密的地心说,妇孺皆知。但大部分人心中的托勒密地心说,也就是那个“所有天体绕着地球转圆圈”的模型,其实并不是托勒密的,而是公元前四世纪前后,柏拉图和欧多克索斯等人提出的。甚至连本轮和均轮也不是托勒密的,而是阿波罗尼乌斯(Apollonius,大约在刘邦那个年代)提出的,以解释行星逆行的现象。同时期的喜帕恰斯(Hipparchus)为了解释夏至太阳远而冬至太阳近,又提出了地球其实不在宇宙圆心中央,而是离圆心偏了一点点的偏心圆模型[1]。
下图中,左边就是大家熟悉的本轮 - 均轮模型,星球 P 在一个小圆上作匀速圆周运动,同时小圆的圆心 C 又绕着中心天体 E 作匀速圆周运动,且 CP 连线保持一个固定的指向(相当于一年转一圈)。右图是简化的偏心圆模型,星球 P 在以 C 点为圆心的大圆上作匀速圆周运动,而中心天体 E 偏离圆心 C 一点点。
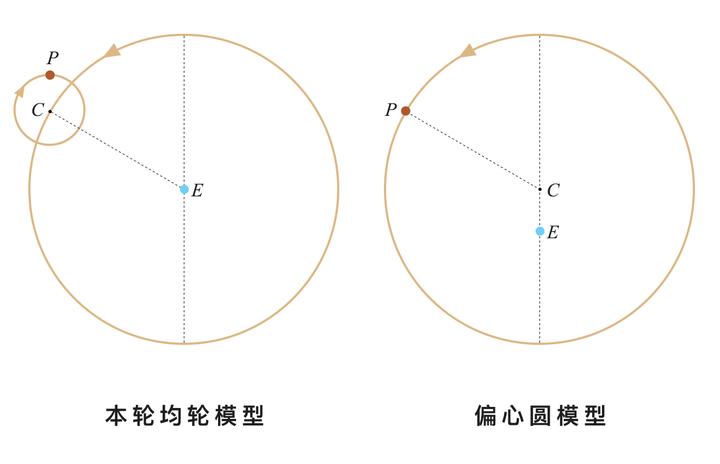
以上这些模型,都建立在两个隐含的假设之上:
- 天体的运动轨迹是完美的圆
- 天体的运动是匀速的
而托勒密的最大贡献,就是打破了天体是匀速运动的这个设定。这可是柏拉图的学生亚里士多德等人坚持的精髓所在。托勒密发现,如果在喜帕恰斯的偏心圆模型上套均轮,其计算出的火星逆行要比实际观测到的有最高达 30 度的误差。
经过分析,托勒密认为,星球 P 其实不是在偏心圆上作匀速圆周运动,而是以另一个点 E’做恒定的角速度的圆周运动(以及均轮上的运动),这个虚拟的点 E’,与地球距圆心 C 等距,托勒密称其为 Equant point(译为均衡点、等距点或均点)。
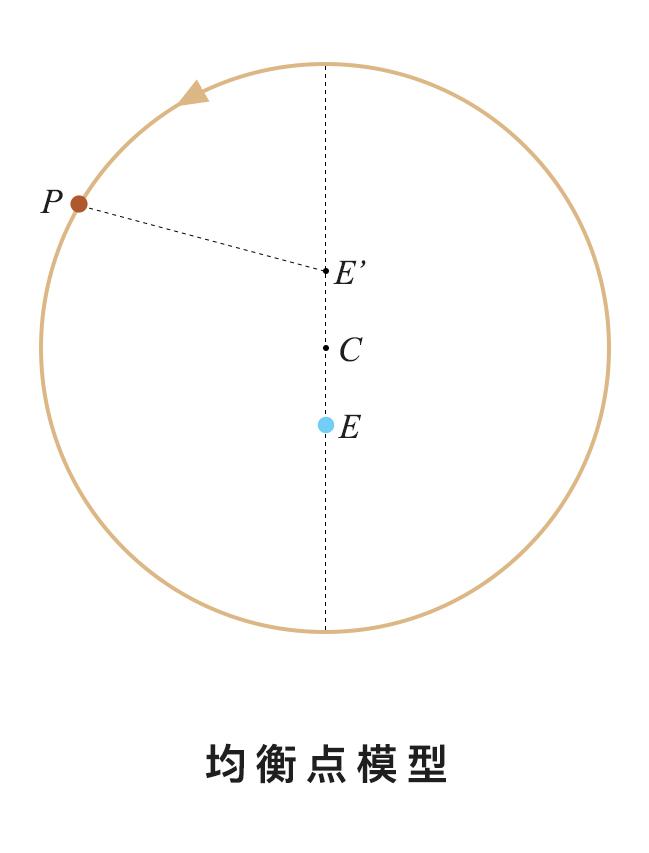
2.开普勒的困扰
现在轮到我们的主角开普勒上场了。开普勒当时是认同哥白尼的日心说的,因为它看上去是那样简洁。但是,让他十分困扰的是,托勒密的模型对天体位置的预言精度,要远远好于哥白尼的日心说模型。
也就是说,虽然哥白尼的日心说模型看上去好美,但不太好用,和实际观测结果相差有点大。如果是你,你会怎么想?
开普勒首先想到,会不会是观测数据出了问题?可是这个观测数据,是由他的老师、最伟大的裸眼观测天文学泰斗、行走的人型高精度天文望远镜第谷·布拉赫在乌拉尼堡多年观测收集的(当然开普勒也参与了火星的观测),他甚至考虑了地平线处大气折射对天体定位的微弱影响,精度那是相当的高。
如果数据没有问题,那只有可能是模型出了问题。当年哥白尼之所以提出日心说,就是对均衡点这一虚拟设定非常的排斥,因为那里空无一物,怎么会凭空出现一个匀角速度的参考点呢?这在数学上说得过去,在物理上却很难解释得通。
那时的开普勒,和哥白尼以及那个时代的许多哲学家一样,还是相信圆是宇宙中最完美的神圣形状,天体的运动轨迹必须是完美的圆。因此他花了很多年的时间,努力将第谷安排他的对火星运动的观测与圆形轨道相匹配起来。
但都失败了。
3.第一次尝试:圆
开普勒注意到,行星的线速度随着离太阳距离的增加而变慢(也就是我们现在所说的,距太阳越远,行星的公转速度就越慢)。他认为,这里面蕴含着物理原理,而不仅仅是一个几何模型问题。(牛顿表示,这个还得等我把万有引力模型研究出来再说)因此,他确信行星运动和太阳有很大的关联,于是他第一步先尝试把均衡点模型中的地球换成太阳。
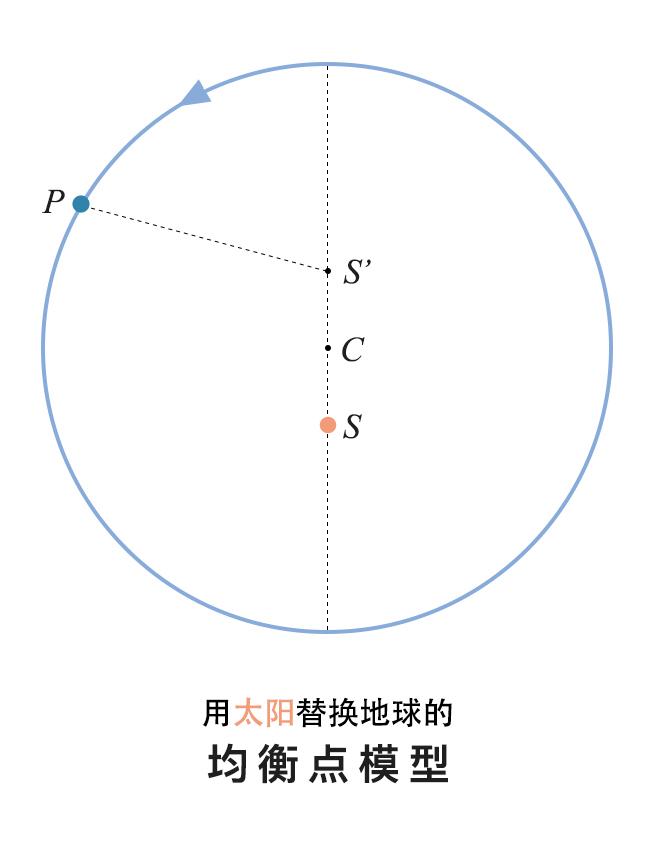
他拿火星为研究对象,设其公转圆半径为 1,把观测数据代入后,算出 SC=0.11332,而 S'C=0.07232。
由于这个时候作为观察者的地球人已经不在圆心那里了,因此还得知道这个圆有多大,才能知道其相对于地球的方位。也就是需要知道火星到太阳的距离。
这也不难。我们令地球 E 到太阳 S 的距离为 1 个天文单位,那么通过观测可以知道日 - 地 - 火的夹角α,由于当时已经通过观测知道了地球 E 和火星 M 的公转周期,因此理论上可以通过连续几次观测来确定夹角β的值(想一想怎么测呢?已知第谷已经观测了 38 年),这样就能算出火星 M 到太阳 S 的距离了。
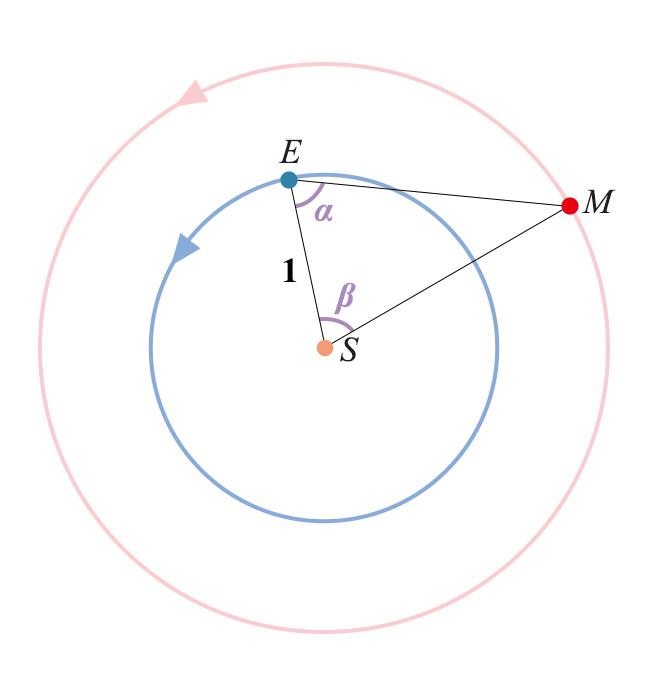
开普勒试着用这个新的日心均衡点模型来预测火星的位置。用它计算得出火星轨道的圆心,确实位于太阳和那个均衡点 E 中间,拿这个模型来预测某个时刻火星的纬度,与实际观测的误差极值仅仅略大于 2',也就是一度的 30 分之一。这个误差对于当时的观测条件来说,已经是非常小非常小了。
但是,在经度的预测上却有着最多高达 8'的误差。
4.第二次尝试:卵形
开普勒没有轻易放过这个 8'的误差。他分析了一下数据,发现这所谓的“误差”出现的非常对称,也就是说,是非常有规律的、都分布在圆的内部。他基于等面积关系做出一个大胆的猜测:天体的运动轨迹并不是完美的圆。是呀,既然托勒密能推翻匀速这一条件,那为什么不能再把另一个假设也推翻呢?
他结合火星在近日点线速度快、远日点线速度慢的情况,猜测轨迹可能是一个卵形,近日点更尖一些,远日点更圆一些[2]:
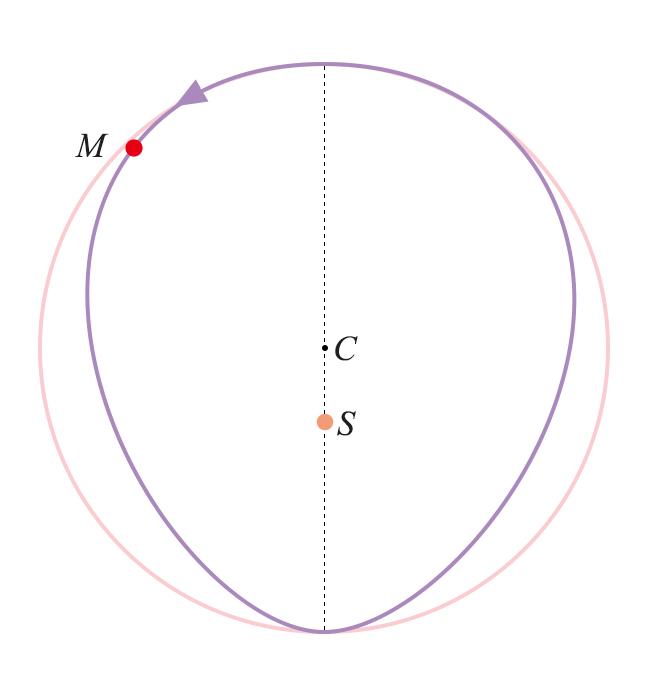
但是把观测数据往这个卵形轨道上套的时候,发现误差并没有变小。
5.第三次尝试:椭圆
开普勒把观测数据又仔细研究了一遍,认为真实的轨道应该在圆与卵形之间的一种光滑曲线。
会不会是一个椭圆呢?
但椭圆是个很难以直观看出的图形,不能说看着像椭圆,就是椭圆了。(而且我们现在知道,火星轨道其实很接近圆,至少比我们手画的圆要圆得多。所以能想到椭圆,并没有我们开插眼那样觉得天经地义显而易见)
开普勒想了很多办法,终于找到了一个难以想到的奇特角度。
他定义火星在(这个疑似椭圆)轨道上的位置为 M,然后将 M 投影到垂直于长轴的外接圆上,得到投影点 D。连接远日点 A 到圆心 C、再到火星投影点 D,连成一个角∠ACD,也就是下图中的那个β。(在现代的天文学中,我们一般用到的是这个角的补角,也就是从近日点 B 到 C 到 D 的“偏近点角(Eccentric anomaly)”。与之相对应的,是真近点角∠BSM,这个角度更容易想到)
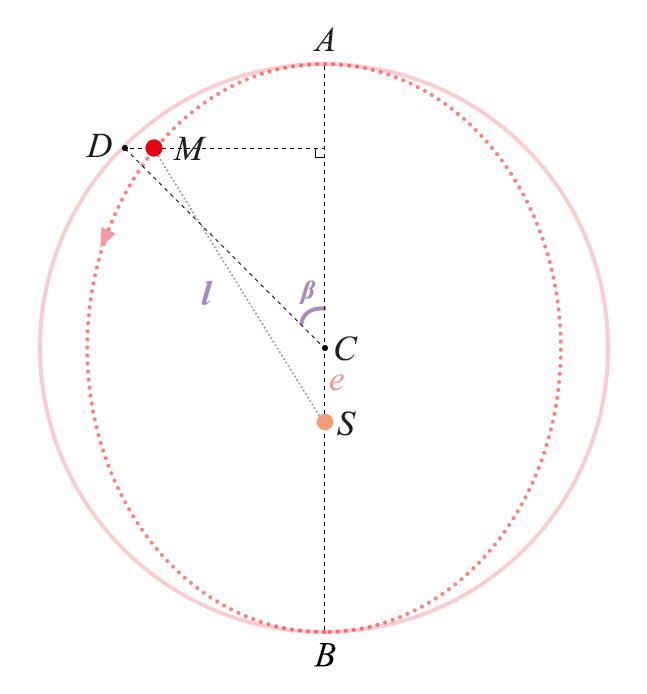
当β=90 度时,易知 M 落在半径 CD 上,不妨设圆的半径 CD 为 1,根据观测数据可以计算出,这时 M 点离 D 的距离最远,或者说这时的曲线的腰最“瘦”,M 所在的短轴(即 2 倍 MC)比整个圆的直径要小了 0.00858[3]。
这里插一句,我们现在知道,这就是个椭圆,半长轴为 1,则半短轴为 0.99571,算出的椭圆离心率为 0.0925,和真实的火星公转轨道离心率 0.0934 非常接近。
但那个时候开普勒并不确定这个曲线就是一个椭圆形。也许你会想,这还用确定?一看就是椭圆啊。不不不,这世界上有太多的曲线看着像椭圆,但其实不是。比如我随便写一个:
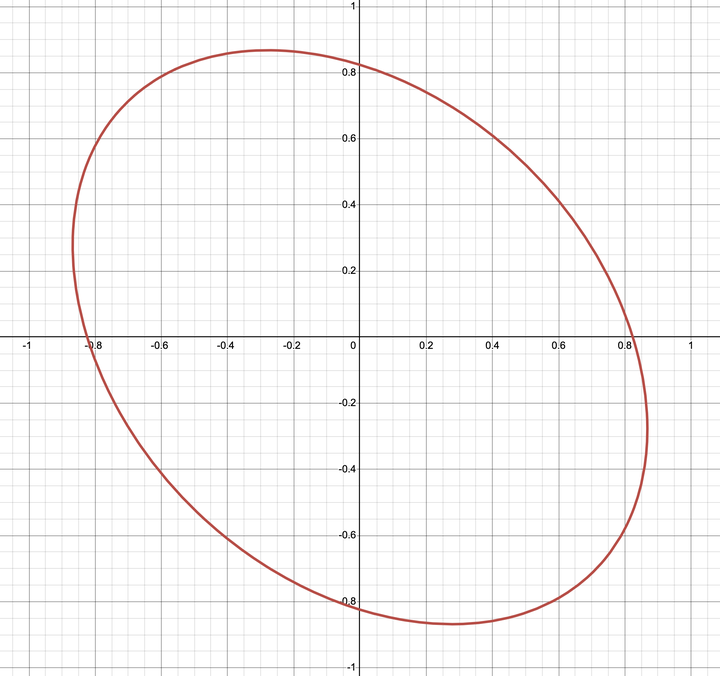
看着非常像椭圆,但其实不是。事实上,它与椭圆的区别极小,用肉眼是看不出的。如果你不相信,可以看下面这个图形:
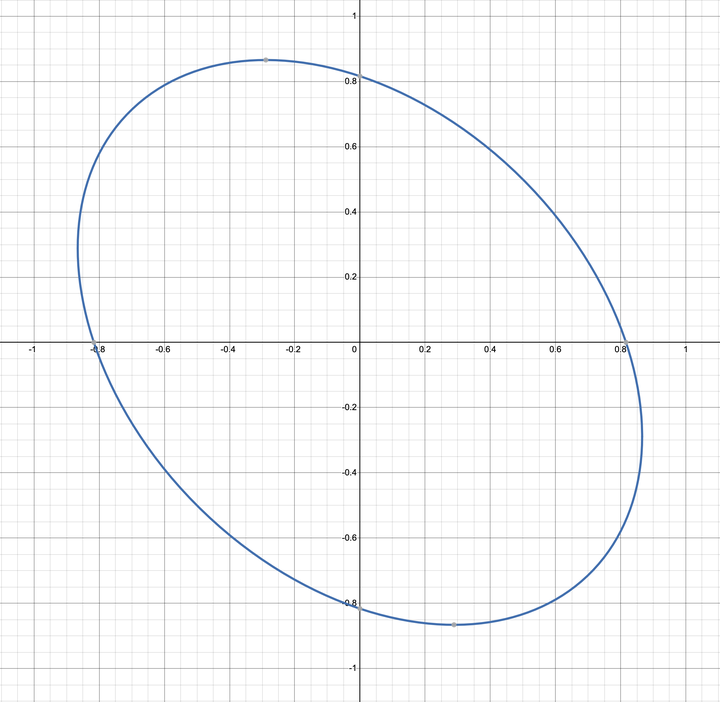
这个是如假包换的椭圆,你能看出蓝色的椭圆和上面那个红色的封闭曲线的区别么?
如果是你,在没有微积分的帮助下,怎么办?开普勒选择用万能的代入法,先代几个点的数值进去试试看嘛,反正观测数据非常翔实。他分别试了比较好算的 45 度、90 度、120 度和 150 度的点的位置。然后,他一瞪眼,竟然发现了一个规律,那就是在这几个角度下,火星到太阳的距离 MS(设为 L),均满足下面这个等式:
上式中的 e,就是太阳 S 到圆心 C 之间的距离,如果是椭圆的话,就是它的焦距(c),由于我们刚才已经把圆的半径、也就是椭圆的半长轴 a 设为 1,所以 e=c/a=c,也就是说,这个 e 在数值上就是椭圆的离心率。
他又试了几个数值,都很满足这个公式,误差非常小。当然,在计算过程中还是走了相当多的弯路,也犯了很多错误,这里就不去说它了。
如果你接触过极坐标,有可能会看出,上面这个等式,可能会是个椭圆。这里写不下,具体的证明过程就略了。
如果你真的想刨根问底, 我就写个大概思路。先只考虑一个象限,设曲线上任意一点的平面座标为(x,y),则有
且由直角三角形可知:
把这两个式子与上面那个等式联立,七里咔嚓一算,就能得到
这明显是椭圆方程的典型形式[4][5]。
6.结论
你能明显看出,上面只是用了归纳的方法,而并不是一个严格证明。
开普勒在给 Fabricius 的信[6]中是这样说的:
The orbit is a perfect ellipse, or at least differs insensibly from such an ellipse.(轨道是一个完美的椭圆,或者至少是与椭圆没什么明显差别的曲线)。
要严格的证明,还得在时间线上等等牛顿和莱布尼茨。
不论怎样,那时根据开普勒的计算公式,对火星公转轨道进行预测,精度可以提升很多了,平均误差只有 2'7",最大误差也只有 5'50"[7]。后来墨卡托在 1676 年的著作《Institutionum Astronomicarum Libri Duo》[8]中,按开普勒的方法又重新算了一遍,轨道平均误差减小到 1'46"。
之所以开普勒能够成功猜到轨道的形状,最大的原因,除了开普勒的数据很翔实以外,关键是他相信,火星等行星并不是由某个长着翅膀的天使或其它什么神灵来推着自己运动的,而是靠着中心天体、也就是太阳的某种力量(就像太阳射出的光一样)来运动的。因此他假设,这个轨迹应该与到太阳的距离和角度有关。
当然,还有一个很幸运的因素,就是火星是八大行星中除水星外公转轨道离心率最大的一个,而作为内行星的水星并不容易观测,所以还是非常幸运的。(还好没观测金星,离心率只有 0.0068)
开普勒的计算精度,远远优于以圆轨道为前提的哥白尼日心说,也优于托勒密的地心说,形式上也比他的老师第谷那个像日心说的地心说的妥协版本要优雅(可惜因为一直没观测到恒星周年视差,被第谷地心说打压了好多年抬不起头来)。因此,逐渐被天文学界接受,成为最好用的轨道预测工具之一,并为牛顿架设好了通向万有引力的台阶。

你竟然读到这里了!谢谢你关注我。

