有点激动,不是因为点赞,而是因为大家对数学的热爱。我能力有限、水平不足(不是套话,真是越学越知道学无止境),所以文中不少错漏,各位大侠在讨论区里面平和、睿智的指出、讨论,和我所见的别的一些知乎的回答下面的评论中,情绪、荷尔蒙、喷子横飞的场景大不相同。果然,喜欢数学的都是好人。我爱数学!
---------------------------------------------- 正文 -----------------------------------------------------------
1 引言
“为什么 1+1=2?”,我眉头紧皱,抚案沉思,答案涌上心头,“存在即合理”,不叫 1+1=2,也会叫 a+b=c,到时候就会有人来问“为什么 a+b=c”。
学了数学之后才发现自己太 naive,纯粹属于“书读得太少,却想得太多”。
2 自然数的构造
数学是数学家构造出来的一个世界,那么自然数的构造就是数学世界的开天辟地。
2.1 选择
我们先放空自己,想象在连空间、时间都一无所有的数学世界里(空间、时间还要在自然数之后才能被创造出来),我们应该怎么去创造自然数?
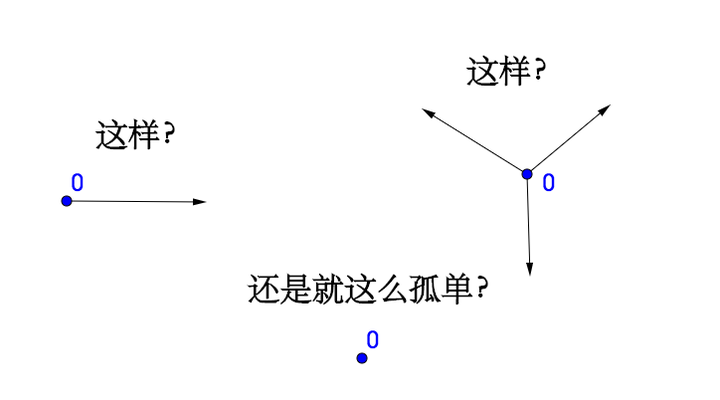
自然数会不会是这样的:
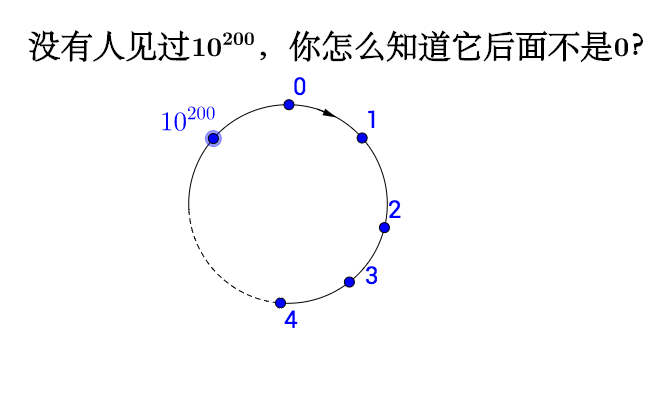
或者是这样的:
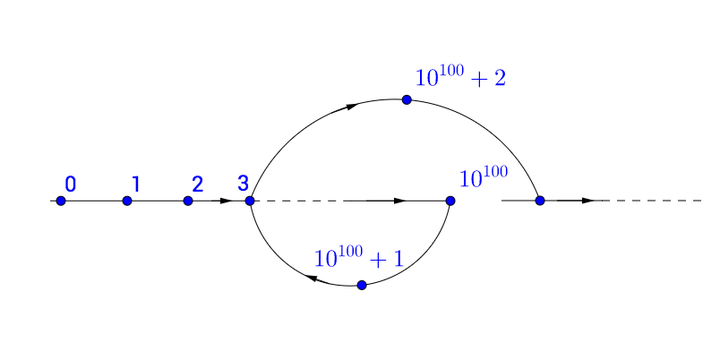
甚至这样:
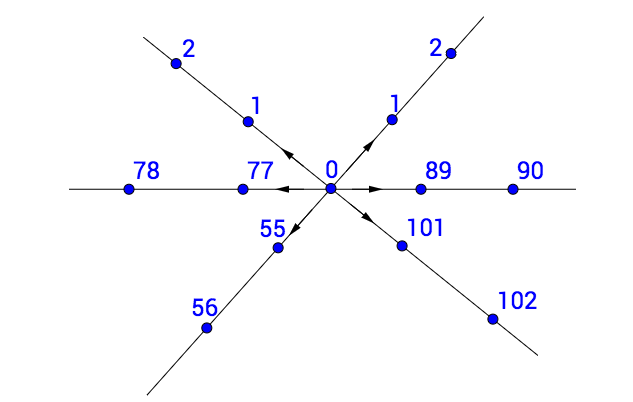
选择不同的自然数体系,那么数学世界会完全不同,大家也知道最后我们做了这个选择:
这个选择是自然而然做出来的,是经过历史考验的,所以我们称之为“自然数”。
你猜猜,外星人会不会做出和我们一样的选择?至少目前看来地球上各个独立发展的文明基本都做出了一样的选择。
2.2 皮亚诺公理
意大利数学家皮亚诺用公理把自然数安放在了数学世界里面。
公理 1:0 是自然数。
空旷的世界有了第一个孤独的元素:

这就是产生整个宇宙的奇点。上帝创世的第一天是不是就是放置下了自然数 0?
然后奇点 0 的大爆炸应该是什么样子的?
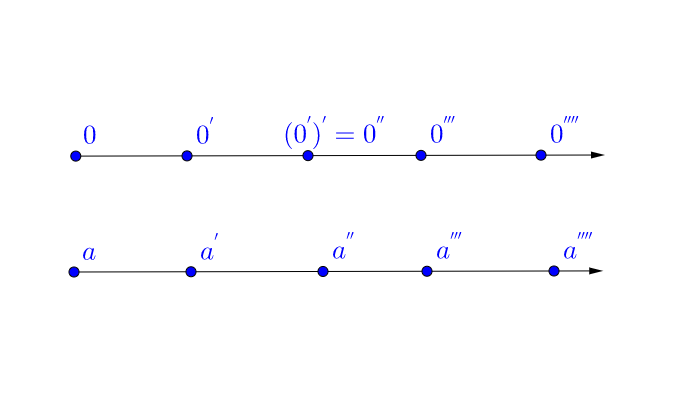
公理 2:每一个确定的自然数,都有一个确定的后继数
,
也是自然数。
这个公理做出了选择:
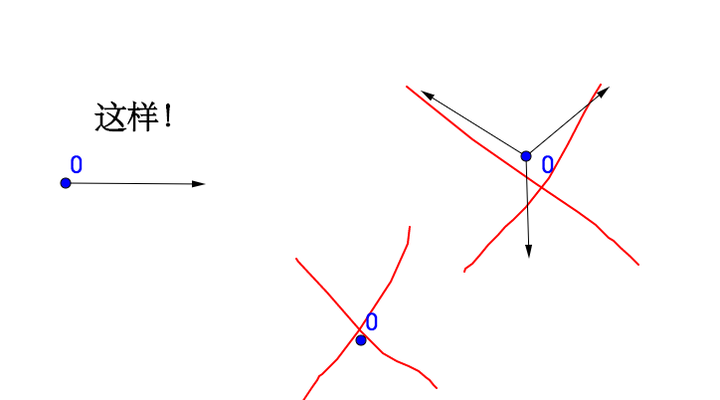
为了避免太过于“迂腐”,“后继数”这个词未加定义的就使用了。
基本上雏形是有了:
但是还是可能长成这种造型:
公理 3:0 不是任何自然数的后继数。
这条公理直接把上面的情况给毙了:
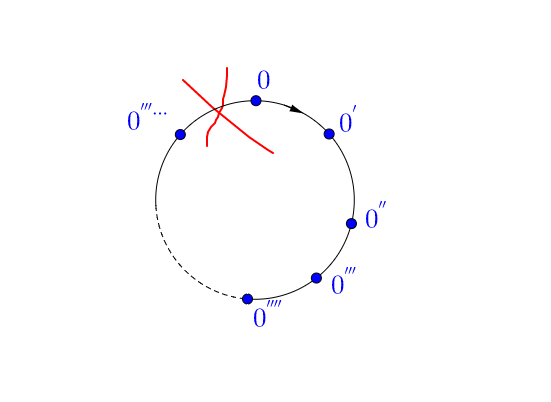
同时这个公理也说明了 0 必须也只能是自然数的第一个数。
但是还是可能长成这种造型(真多事啊):
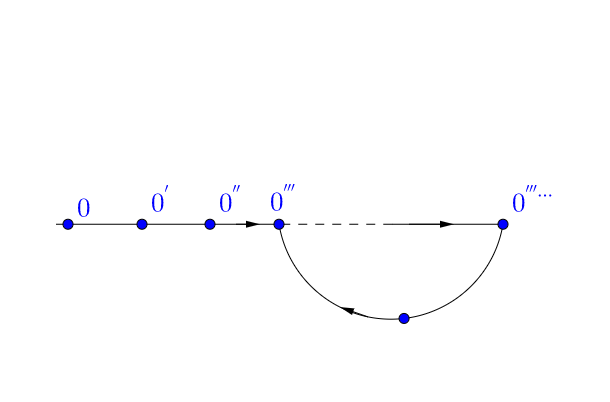
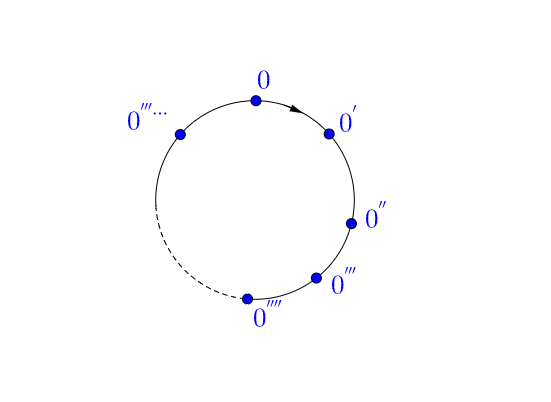
公理 4:不同的自然数有不同的后继数。
这个公理可以避免上面的情况出现:
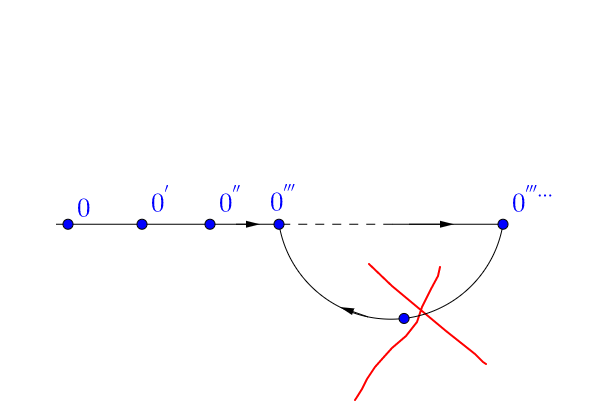
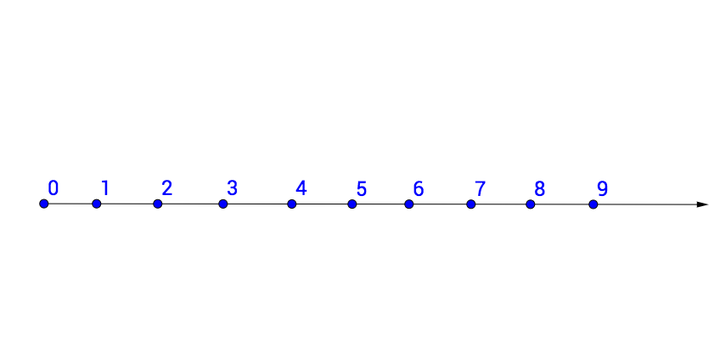
我们终于可以一个数一个数的数下去了。
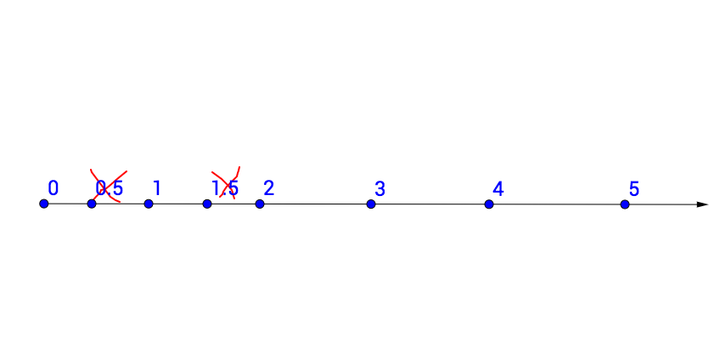
但是现在就全是自然数了吗?这样行不行:
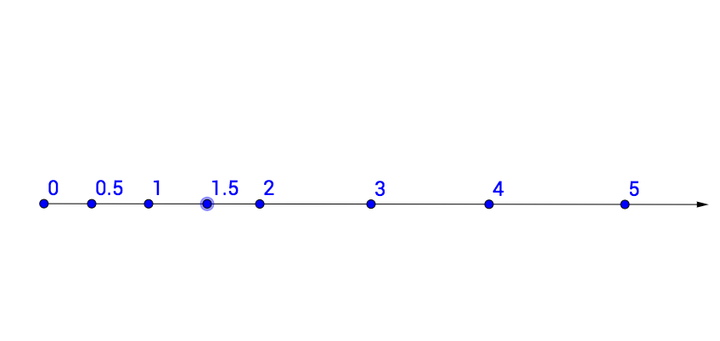
这个数系:
{0,0.5,1,1.5,2,3……}
这个数系满足公理 1-4:
- 0 是自然数。
- 每一个确定的自然数
都有确定的后继数
,
也是自然数。
- 0 不是任何自然数的后继数。
- 不同的自然数的有不同的后继数。
但是 0.5 这样的数不是自然数啊,我们一定要干掉它。
于是又加上一个公理:
公理 5:任意关于自然数的性质,如果证明了它对自然数 0 是对的,又假定它对自然数 n 为真时,可以证明它对为真,那么命题对所有自然数都真。
这里有点绕,自然数都没有构造完,自然没有办法定义具体的自然数性质,这个公理就是说当以后我们定义了一个自然数的性质,自然数都要满足。
并且,这个公理就是数学归纳法!
感受一下这个命题:
是自然数,那么
是自然数,并且
大于等于
。
这个是我们的自然数的一个性质,
,
,不满足这个性质,干掉:
上面给出了一个通俗的说明,下面为有疑问的朋友进行更严格一点的说明,一般来说会有如下疑问:
- 0.5 没有定义,怎么就出现了?
- 0.5 不过就是一个命名而已,我可以规定 0.5 也是自然数,0.25 也是自然数,并且 0.25 排在 0.5 的后面。
我们从这个角度来看待公理 5:公理 5 就是数学归纳法,用数学归纳法可以证明的定理,如果某个数不符合此定理,则一定不为自然数。
对于 0.5 的出现这么来考虑,我们先定义了自然数集,然后又用自然数集扩张为有理数集,然后在有理数中挑一个数,比如说 0.5,因为自然数本身是有理数的子集,所以我并不清楚 0.5 是不是自然数,但是我这么检验,其平方为 0.25,对于自然数不可能平方小于自身,所以它不是自然数。
公理 5 也将在接下来的加法定义中发挥作用。
2.3 命名
皮亚诺公理定义了什么是自然数:他们是这样{
},这样称呼起来太麻烦了,历史上早就把它们的名字准备好了,就是{
}:
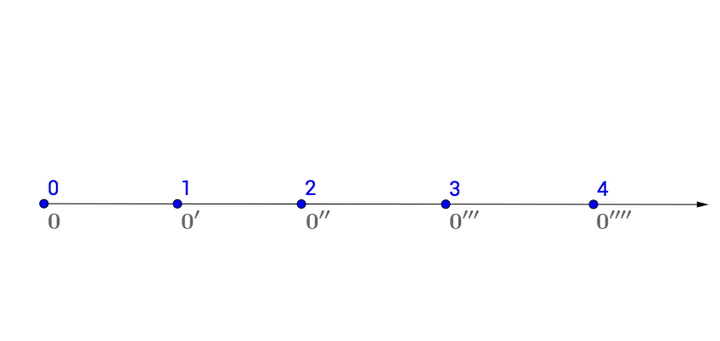
当然也可以叫别的,比如英语里面就是 one、two、three、four、
。
3 加法
只有自然数的数学世界仍然死气沉沉,增加的加法让数字与数字之间开始有了化学反应:
定义自然数的加法:设 m 是自然数,我们定义 0+m:=m.如果定义 m 加上 n:=m+n,那么
要证明
也是自然数,就需要用到公理 5。
我们来计算一下 3+2 的值:
计算
的值就是计算
的值。
所以有
。
加法就像这样:
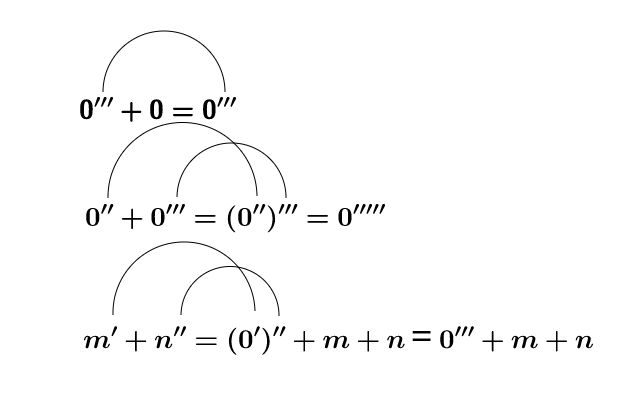
现在我们终于可以来解答 1+1 为什么等于 2:

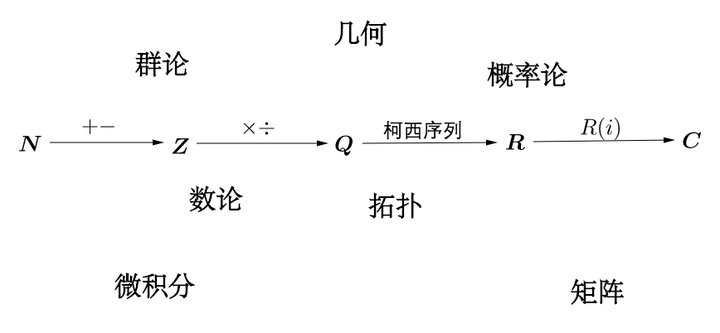
4 大爆炸的继续
自然数和加法是数学世界的根基(当然还有集合论等,忍不住还是严谨一下),在这个基础上数学世界越来越辉煌,这就是为什么需要证明“1+1=2”::
5 思考
为什么数轴是直的, 而不是长成这样:
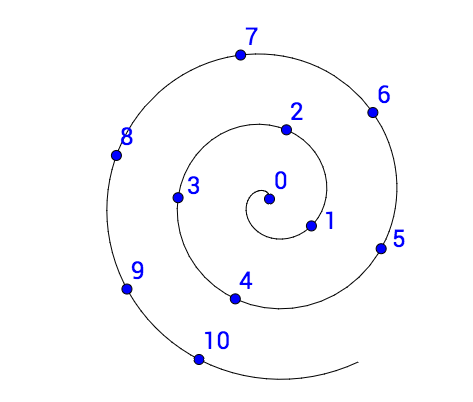
这倒没什么正确答案,不过确实有一些数学原因。
思考是数学真正的乐趣。
参考文献:《陶哲轩实分析》

