什么是孤子？什么是孤子解？ - 趣闻

什么是孤子？什么是孤子解？

知乎精选 2024-06-29 02:00:13

笠道梓，认识的价值是我们所在意的东西。

看一个非常简单的物理中的孤子解，然后考察它的性质。首先写一个 1+1 维经典场论，它的 Lagrange 量密度

$\mathcal{L}=\frac{1}{2}\partial_{\mu} \phi\partial^{\mu} \phi-\frac{\lambda}{4}\left(\phi^2-v^2\right)^2,\quad v=\sqrt{\frac{m^2}{\lambda}}$

求出运动方程

$\frac{d^{2} \phi}{d t^{2}}-\frac{d^{2} \phi}{d x^{2}}=-\lambda\left(\phi^{2}-v^{2}\right) \phi$

讨论它的静态解，也就是令

$d\phi/dt=0$

。显然当势能取最小值，即

$\phi(x)=\pm v$

，我们有两个独立的基态解。若取边界条件

$\phi(\infty)=v ,\ \phi(-\infty)=-v$

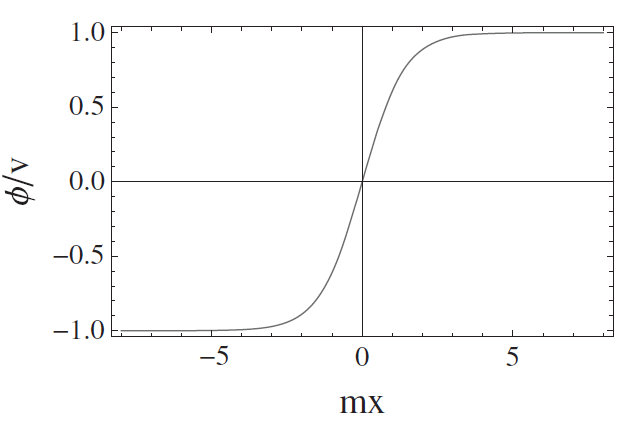
，会有一个孤子解

$\phi(x)=v \tanh \left[\frac{m}{\sqrt{2}}\left(x-x_{0}\right)\right]$

这称为 kink，其中

$x_0$

是积分常数，可以看作孤子的位置，

$x_0=0$

时的图像如图 1。当然取相反的边界条件也可以得到孤子解

$\varphi(x)=-\phi(x)$

，称为 antikink。

图 1

能量密度为

$\begin{aligned} \epsilon&=\frac{\partial \mathcal{L}}{\partial(\partial_0 \phi)}\partial_0\phi-\mathcal{L}\\&=\frac{1}{2}\left(\frac{d \phi}{d t}\right)^{2}+\frac{1}{2}\left(\frac{d \phi}{d x}\right)^{2}+\frac{\lambda}{4}\left(\phi^{2}-v^{2}\right)^{2}\\&=\frac{m^4}{2\lambda} \text{sech}^4\left[\frac{m}{\sqrt{2}}(x-x_0)\right] \end{aligned}$

图像如图 2。

图 2

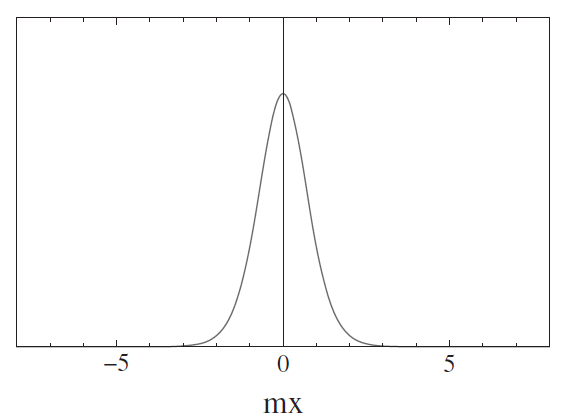
能量的局域性暗示孤子可以被看作一种粒子。接下来积分求出总能量

$E=\int_{-\infty}^{+\infty}\epsilon dx=\frac{2 \sqrt{2}}{3} \frac{m^{3}}{\lambda}$

我们对这个解作 Lorentz 变换：

$\phi(x, t)=v \tanh \left[\frac{m}{\sqrt{2}} \frac{\left(x-u t-x_{0}\right)}{\sqrt{1-u^{2}}}\right]$

这时重新算一下总能量，发现任意时刻都有

$E'=\frac{E}{\sqrt{1-u^2}}$

那么这个解就可以被看作是具有能量

$E$

，以速度

$u$

运动的粒子。很重要的是，随着时间推移，场和它的能量密度的构型仅仅发生了中心的平移，并没有发生耗散，kink 确实就像是粒子。它像是不受任何阻碍地在运动，因而称为孤子。

此外，这个粒子还具有某种守恒的拓扑荷，因而又称为拓扑孤子。要看到这一点，首先定义拓扑流

$J_{\mathrm{top}}^{\mu}=\frac{1}{2 v} \epsilon^{\mu \nu} \partial_{\nu} \phi$

对应的拓扑荷为

$Q_{\mathrm{top}}=\int_{-\infty}^{\infty} d x J^{0}=\frac{1}{2 v} \int_{-\infty}^{\infty} d x \partial_{1} \phi=\frac{1}{2 v}[\phi(\infty)-\phi(-\infty)]$

于是 kink 带有 +1 的拓扑荷，而 antikink 带有 -1 的拓扑荷。有限能量的过程不可能改变场在无穷远处的渐近行为，因此这个拓扑荷是守恒的。这个守恒荷来自基态空间和场构型的非平凡拓扑结构，而不是根据 Noether 定理来自某种连续对称性，因而称为拓扑荷。

凝聚态和高能场论中的 kink，vortice，monopole，domain wall，skyrmion，instanton，宇宙学中的 cosmic string，都是孤子。

更新：多说一些拓扑荷的事情。

就像用规范场的 Noether 荷区分不同类型的基本粒子，我们也考虑一些守恒量，以区分不同类型的场的孤子解。既然我们是考虑一个能看作粒子的场构型，那么能量的局域性要求能量密度在无穷远处趋于零。因为有限能量的过程无法改变场在无穷远处的行为，所以我们只需要场在无穷远处行为的拓扑分类。

我们将场

$\phi$

看作是

$\mathbb{R}^d$

到它取值构成的流形

$Y$

的映射，孤子解的渐近行为

$\phi^\infty$

就是

$\mathbb{R}^d$

上无穷远处的球面

$S_{\infty}^{d-1}$

到场处于基态时的取值构成的子流形

$\mathcal{V} \subset Y$

的映射。我们用

$\phi^\infty$

的同伦类，也就是同伦群

$\pi_{d-1}(\mathcal{V})$

的元素，区分不同类型的孤子解。

回到这里

$d=1$

的情形，

$S_{\infty}^{d-1}=\left\{ +\infty,-\infty\right\}$

，

$\mathcal{V}=\left\{ v,-v \right\}$

，

$\pi_{0}(\mathcal{V})$

也就是拓扑上不等价的基态集合，场构型也就是

$\pi_{0}(\mathcal{V}) \times \pi_{0}(\mathcal{V})$

的元素。这里

$\mathcal{V}$

包含两点，就应该有 4 种拓扑上不等价的构型。假设场由

$\left(v_{1}, v_{2}\right) \in \pi_{0}(\mathcal{V}) \times \pi_{0}(\mathcal{V})$

描述，如果

$v_1=v_2$

，它表示一个全局的基态

$\phi(x)=\pm v$

；如果

$v_1 \neq v_2$

，它表示非平凡的孤子解

$\phi(+\infty)\neq \phi(-\infty)$

，根据

$\phi(\pm \infty)$

的具体取值，可以是 kink 或 antikink。这里定义的拓扑荷就是反映

$\phi^\infty$

同伦类的一个拓扑不变量。

对

$d=2$

的情形，我们用

$\pi_1(\mathcal{V})$

，也就是

$\mathcal{V}$

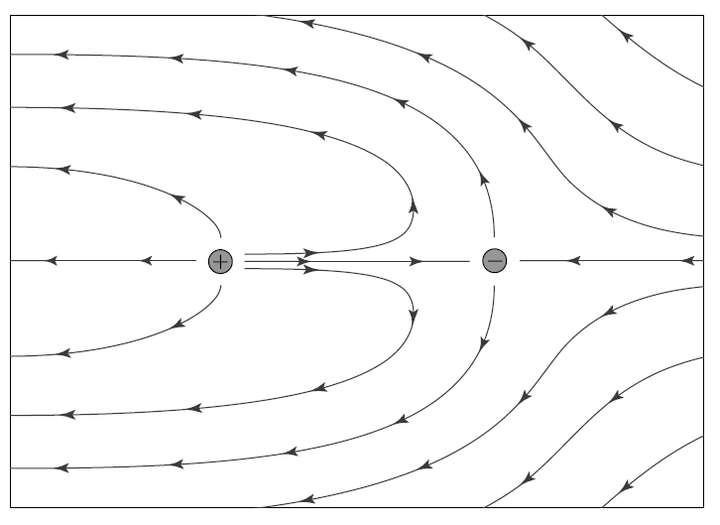
的基本群，来分类场构型。它的非平凡元素有 vortex 的特点，例如图 3 二维 XY 模型中的自旋构型，相应的拓扑不变量就称为缠绕数。

图 3

规范场论中常常用 Chern 数来分类孤子。它们是 Chern 形式在全空间上的积分，Chern 形式是由势

$A$

和场强

$F$

构造的规范不变的偶数次微分形式，局部上可由 Chern-Simons 形式的外微分给出，更多内容可以参看 @Again 的回答

瞬子与轴矢流反常以及 U1 problem 如何联系在一起？

以及 @史诗生物的专栏

从超对称开始的异世界物理

References:

E. J. Weinberg, Classical Solutions in Quantum Field Theory: Solitons and Instantons in High Energy Physics, Cambridge, 2012.

N. Manton & P. Sutcliffe, Topological Solitons, Cambridge, 2004.

查看知乎讨论