失踪人口回归！继续开更！

这个问题困扰了我很久，我看同济的高等数学教材，这一段内容看的是云里雾里，复习考研看复习全书，里面也是来了题目就上公式，没有看到逻辑演绎的过程，学习的非常痛苦，绝望之下，看了国外的数学教程和公开课，总算在脑袋中有了直观的数学直觉，希望能给题主一些帮助。

（另外，我还是多说几句，考研都推荐李永乐的复习全书，我觉得是人云亦云，李永乐的书确实非常适合考研复习，但是前提是你必须有扎实的基础，否则你会觉得密密麻麻的定义定理让人想放弃，没有思辨，没有演绎，还有不推荐数学基础不好的同学考研看同济的数学，这些书虽然严谨，但是总是为了证明一个问题而去证明一个问题，从而让人觉得非常晦涩，所以强烈推荐时间充足的同学先读国外优秀的数学书籍，从一个问题的起源出发，为什么人类要提出这个问题，这个问题是为了描述和解决什么，一步一步逻辑上的推进最后给出最后的结论，让人感受到数学根本就不是一件特别让人头疼的事情，反而是一种思维上的享受）。

正文从这开始。

我的整个讲解大纲是这样的：

曲线的散度和通量 ---->曲面的散度和通量 ---->曲线的旋度和环量 ---->曲面的旋度和环量

哦有件重要的事情忘了说，通量在国内的书上一般称为 第二类面积分（我特别想吐槽这个称呼），我建议大家不要记什么第一类第二类这种完全意义不明的东西，当然因人而异。

首先一个大的思维前提，通量是和散度联系在一起的，环量（也就是题主说的环流量）是和旋度联系在一起的。

我们先说说曲线通量和散度。我们假设有一个向量场 F，他大概如下图所示一样：

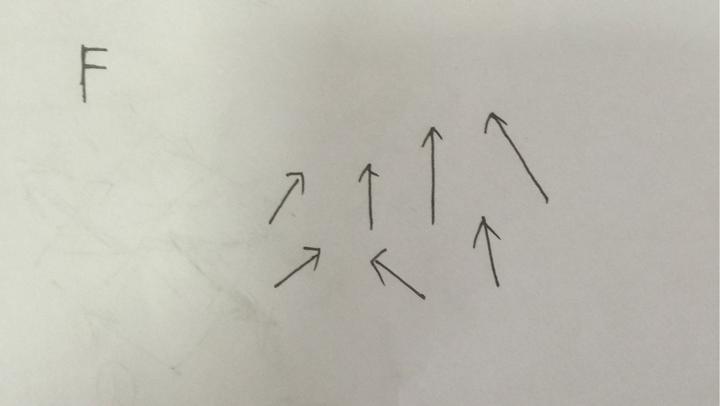
可以看到这些向量有长有短（大小不同），并且方向也五花八门，现在在这个向量场中，出现了一条曲线 L：

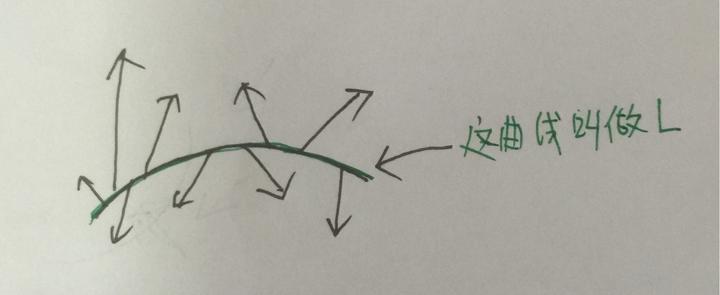
好，那么题主你想想看，这些向量，既有大小，又有方向，那么他们是不是有移动的趋势呢？既然移动，就肯定会通过这条曲线 L，那么有的朝着外面通过，有的朝着里面通过，那么就会相互抵消，于是我们就运用微积分的思想，整理出了如下的通量公式：

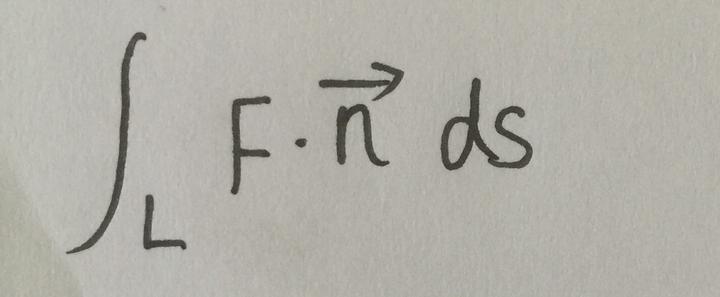
我们把这一段曲线分成无数小段，近似于一小段直线，那么这一小段长度为 ds，n 是这一小段直线的单位法向量，方向根据其顺时针运动还是逆时针运动有关，那么每一小段上向量 F 在法向量上的分量（F·n）乘以这一小段的距离 ds，然后加起来就是这一小段曲线的通量。到这里，题主脑海中应该形成一个数学直觉就是，通量，就是通过的量！

那么通量这个东西为什么说和散度联系在一起呢？回顾怎么求一点的散度：设二维平面上一点处的向量 F=P(x,y)i+Q(x,y)j，那么这一点的散度为：

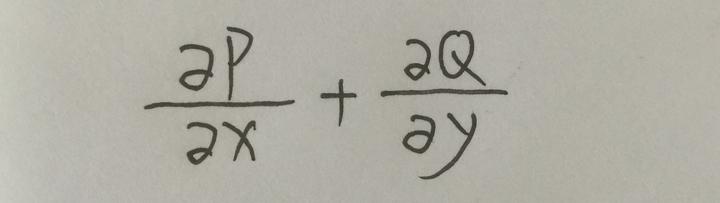
但是凭什么说向量沿 x 轴和 y 轴的分量的偏导数就是散度？想象一下：当一点处向量分量沿各自方向的偏导数的和为正时，说明这一点处的向量，非常讨厌这一点，想要迫切的离开这一点，正数越大离开的想法越强烈；当为负时，说明这一点的向量很喜欢这一点，他虽然不愿意离开，但是奈何人家要赶他走，于是他走的脚步很慢，负数越大留下的愿望越强烈；当为 0 时，这一点的向量对这一点没有任何感觉，你要我走，那我就走咯，不紧不慢的保持着原有的样子。

所以散度，在脑海中可以形成的直觉就是，这一点的向量离开这一点的愿望的强烈程度。

------------ 最近很忙，慢慢补充 -----------

我们已经知道曲线上通量和散度的意义了，那么我们如何建立他们的联系呢？

我们在脑海思考这样一个场景：一个封闭的城市爆发了丧尸病毒（封闭曲线），城市中所有的人都用各种方式逃离这个城市（不得不离开自己的家园），有的人早就厌烦这个破地方，跑的飞快（散度为正），有的人热爱自己的家园，舍不得离开（散度为负），人心险恶，逃跑方向相反的人相遇时，会互相残杀争夺资源（不同点的散度会相互抵消），最后总有一部分人会成功的通过这个城市的边界（通量），逃离这个城市。

这个例子虽然不太恰当，但是我想应该该能帮助大家建立散度和通量联系的直观直觉，内部你们怎么争夺是极其复杂的，我不管，我只用看看最后有多少人通过边界就行了。散度和通量的联系是否就是应该这么直观呢？

当然这里我们要用数学的语言来描述散度和通量的关系，大家还记得可恶的高斯公式吧，不过那是描述三维曲面的，在二维平面上，一个封闭曲线的高斯公式长这样（之前笔误把 Pdy 写成 Pdx 了，重新更正了一下）：

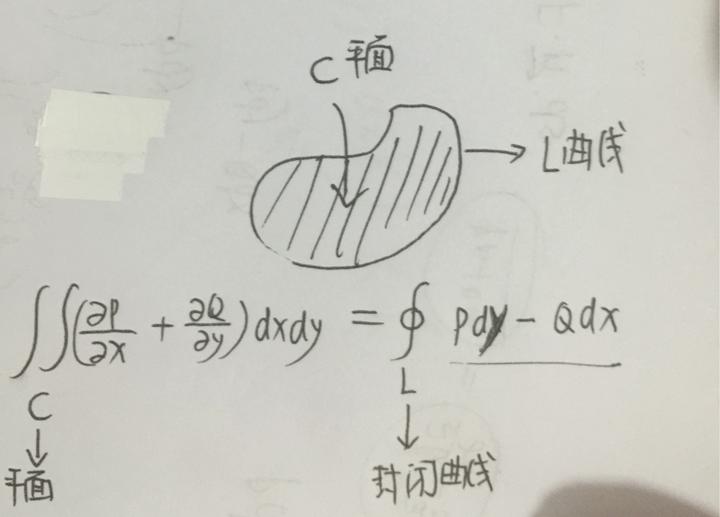
很奇怪对吗，虽然考研并不考二维平面的高斯公式，但是我就是对这个结果纯粹的好奇，最后成功推导出这个结果，就像多年的老便秘释放的感觉，非常爽。

来让我们用之前的知识推导它！

首先这个平面上各点的向量为 F=P(x,y)i+Q(x,y)j，那么式子左边就是这个平面各个点散度的积分，根据我们之前建立的联系，他应该等于这条曲线的通量的积分，关键的问题来了，我们怎么求这条曲线的通量？也就是说，式子右边我是怎么写出来的？

首先我们把这个封闭曲线无限分割，最后会得到一条直线：

这条直线用向量如何表示呢？显然沿着 x 方向的微分分量为 dx，沿着 y 方向的微分分量为 dy，所以这一小段直线可以表示为 dxi+dyj，我们知道通量是这一点的向量在其法向量的分量乘以这一段的距离，那么这一段的法向量是什么呢，确实是个难题，但是如果你还记得向量的叉乘就有知道如何解决这个难题了：

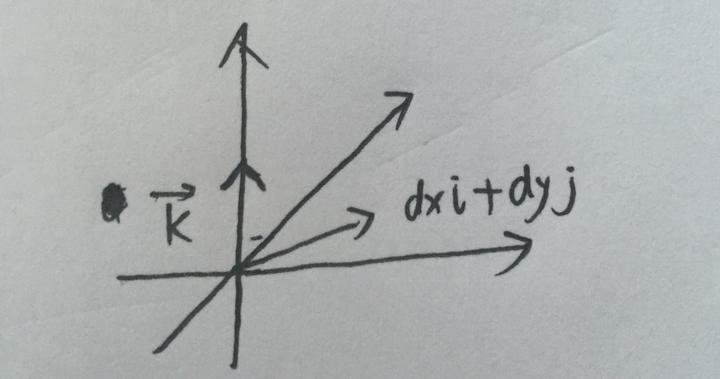
看见那个 z 轴的单位向量 k 了吗？它是垂直于 dxi+dyj 的！那么我们还记得叉乘会得到一个垂直于两个向量的新向量，这个新向量不就是我们要的法向量吗？！

于是：

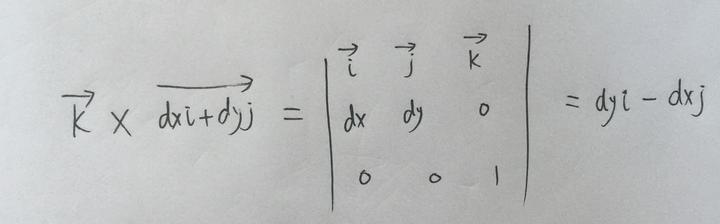
注意得到的这个向量不是n，而是nds，因为 n 只是个单位法向量，而我们得到这个是单位法向量乘以长度后的向量（还不明白的话可以给我私信或者评论）。

那么我们根据通量公式用这个向量点乘 F：

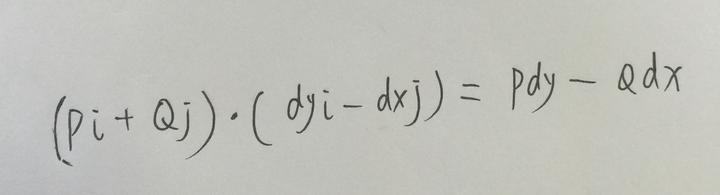
这只是一小段的通量，把这家伙一积分，不就是整段曲线的通量吗？！

好了，困扰人的二维高斯公式被我们 KO。（百度上看到有好多人不懂高斯公式是如何退化到二维平面上的，所以顺便帮大家解决掉这个问题，希望那些在百度中没解决问题的朋友也能搜到我这儿）。

另外，千万不要晕圈，看到有朋友把这个高斯公式的二维退化看成了格林公式，千万不要搞混，格林公式解释的是二维平面上旋度和环量的关系，而这个二维高斯公式是解释通量和散度的关系，务必不要搞混，仔细多看一下我的推导过程^_^。

明天将讲解曲面通量和散度，以及考研常考的高斯公式，如果你曾经被这个高斯公式虐过，一定不要错过我明天的讲解哟。

---------------------- 分割线，继续 ----------------

昨天已经把曲线的通量和散度解决掉了，今天我们把将其推广到三维曲面上，来看看三维曲面上通量和散度的联系。请看如下曲面：

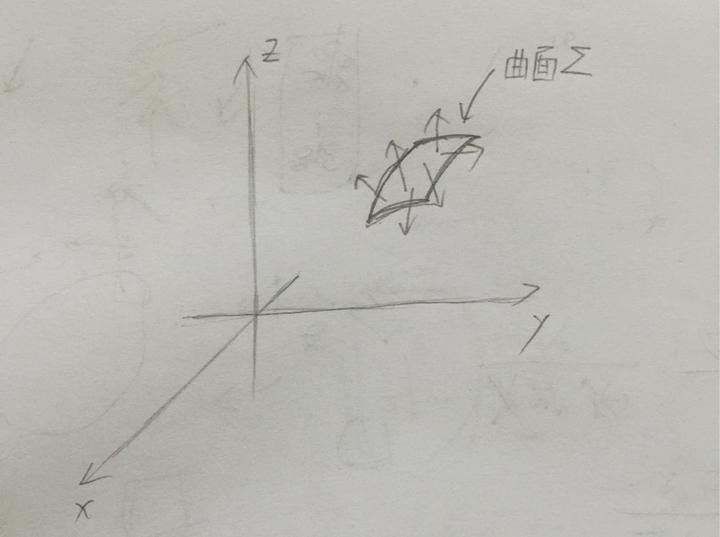
假设曲面上任意一点坐标为(x,y,z)，那么这一点处的向量为 F=P(x,y,z)i+Q(x,y,z)j+R(x,y,z)k，我们如何求这些向量通过这个曲面的量呢？还是按照微积分的老路子，先微分了再说：

注意我们对曲面进行微分后，得到的是一个空间中的平行四边形，我们设这个平行四边形的面积为 ds，它的单位法向量为n，那么根据通量公式，这一个小平行四边形的通量就应该是 F·nds，但是我们立刻发现我们遇见了一个难题，我们既不知道法向量n怎么求，也不知道面积 ds 是多少，不过我们之前在二维平面上是怎么获得法向量的还记得吗？叉乘！这个家伙在这儿能帮上我们忙吗？能！

我们首先看看这个小平行四边形，能让我们挖掘哪些东西：

----------这里补充关于下面这张图的解释----------

这张图有同学表示看的不太明白，没有搞清楚那里那两个偏导数的作用，这里解释一下，因为在三维空间中，z 的取值是由 x 和 y 共同决定的，所以当由 A 点到 C 点时，x 增加 dx，y 没有增加，但是 x 增加引起 z 增加，所以 z 方向上增加了 dx 乘以 z 关于 x 的偏导数；A 到 D 同理。

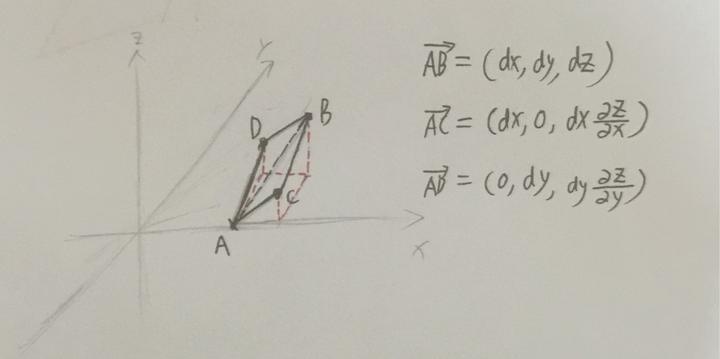
我们假设曲面由 z=z(x,y)表示，那么我们从一个微分后的平行四边形上可以挖掘出这三个向量，那么我们怎么才能求垂直于这个平行四边形的法向量呢？根据叉乘定义我们可以知道，用 AC 向量 叉乘 AD 向量，会得到一个垂直于平行四边形且大小为平行四边形面积的向量（为什么？请百度一下叉乘的定义，虽然我也会证明但是就不展开了）！这不是就是nds 吗？！于是我们就知道：

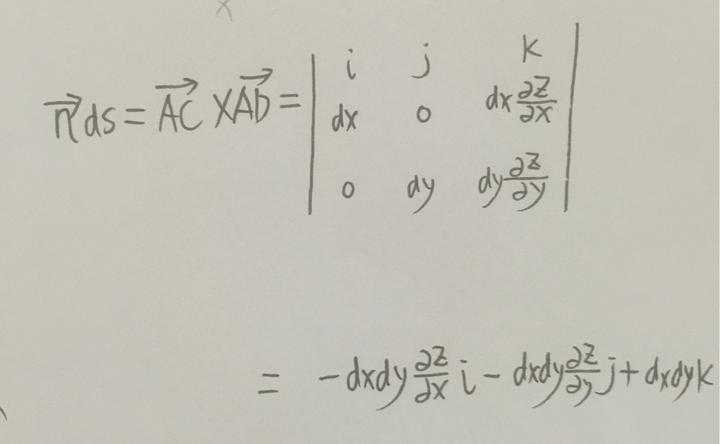
现在我们用 F 点乘 nds，我们会得到什么呢？

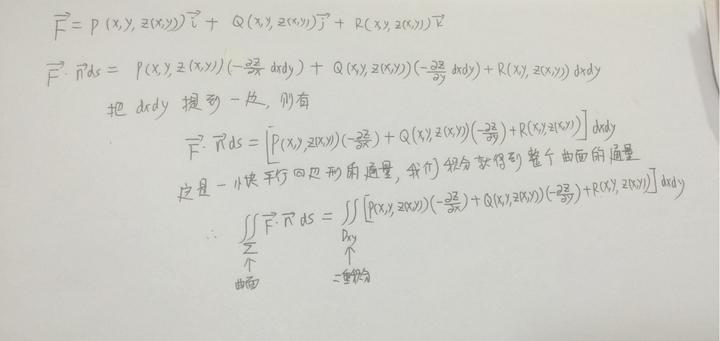
大功告成了吗？还差一点点，之前我们用 AC 叉乘 AD 得到一个 nds，但是如果我们用 AD 叉乘 AC 同样也会得到一个 nds，当然这两者的大小相同，方向相反，所以根据方向不同，有正负之分，所以加个正负号就完美了，这就是完成品：

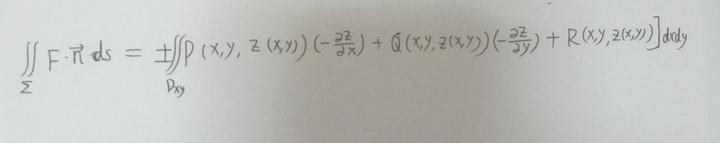
有点陌生？这个式子还有一个样子，长这样：

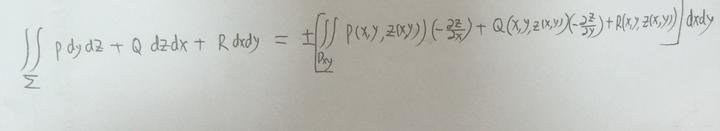
--------------- 从这里开始来理解什么是旋度 --------

旋度一直是考研数学一中很招人厌的东西，莫名其妙的定义，又长又臭的形式，总是被大家当作偏僻考点，然而 2016 年数学一确出了一个旋度的考题，很多人骂出题人故意出偏僻的考点，但是实际上，那道题是一道极其简单的送分题，但是由于许多人没有理解旋度，也懒得背公式，自然是得不到分了。

这里我请大家放心，旋度只要一旦理解了是什么东西，那个又臭又长的式子根本用不着背，你可以直接很轻松的写出来。

在正式开始讲旋度之前，我必须请大家先移步我另一个关于格林公式理解的答案，因为我接下去关于旋度的理解，是以我对格林公式的理解为基础而推导出来的。

关于格林公式的理解：

https://www.zhihu.com/question/22674439/answer/165988374

好，在理解了格林公式的形式之后，我们进一步的提出一个问题：你们有没有发现，格林公式描述的其实是一个旋转？

你看，格林公式要求的是封闭区域，求这个封闭区域上沿着边缘一圈的向量做功，更抽象地说，就是沿着一圈的环流量。无论你之前想过没有，但是现在你必须想到，格林公式描述的，确确实实是旋转而产生的环流量。（有些同学不理解做功为什么是流量，实际上流量一个抽象的概念，意在描述“一个向量沿某方向运动”，有时候我们为了便于理解，就把这个向量想成力，那么就会把“流量”这个抽象的概念变成具体的做功，但是运动的向量可不仅仅只能是力，还可能是其他的东西，所以在这里我们用更抽象的流量来帮助大家建立统一的认识）

另外，高等数学是其他许多复杂数学分支的基础，高等数学的基础打得越牢，其他更复杂的数学才有扎实的保障，所以如果你正在学习诸如数学分析等这样的课程但是学的十分难受，有可能是高等数学的基础就没有打牢固，没有学会如何分析一个问题的方法和思维。

题主的这个问题比较庞大，需要花时间慢慢来讲，今天就先到这儿啦。

另外希望大家对于公式，千万不要机械记忆，死记硬背，你看看咱们这么推导公式，是不是深深地感受到数学的逻辑优美，直接背公式只会让你很讨厌数学的。

先写到这儿吧，之后慢慢补充。