谢邀，这是个好问题。

祖氏父子对球体积的计算是基于刘徽的工作的。

正方体的体积非常好求，而刘徽试图从正方体体积入手，去找出正方体内切球与正方体的体积的比例关系，这样就知道了球体积公式。

刘徽提出了这样一个办法：首先有一个正方体，在正方体内作两个轴线互相垂直的圆柱，而圆柱的直径等于正方体的边长，把这两个圆柱相交的部分提取出来，叫做“牟合方盖”。

长这样

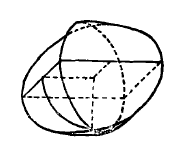
如同把正方体等分成八个小立方体一样，可以把牟合方盖也分成八个小块，就像……呃……切开的面包？感受一下。而正方体的内切球就恰好在这个牟合方盖的内部。

这玩意又方又圆，横着切怎么都是方的，竖着切怎么都是圆的，设计师朋友可以学习一个用来应付甲方。

我们就当他是面包吧，味 O 美有个长这样的奶油面包，特别好吃。

然后再把这个面包横着切，切面总是正方形的。稍微想想就可以明白，这个正方形的内切圆恰好就是从同样的高度下刀的球形面包的截面。

正方形与其内切圆的面积比例是 4:π，体积是一层一层的面累积起来的（这里有原始的微积分思想），那么，由正方形堆起来的牟合方盖的体积，与由正方形内切圆堆起来的球的体积的比例，也是 4:π。

其实这里刘徽就已经用到了祖暅原理，然而他没总结出一般形式来……

这样，我们只要知道了牟合方盖的体积，就可以求出正方体内切球的体积了。

然而刘徽怎么算都算不出牟合方盖的体积，瞎几把算了一下还算错了，最后没办法，说：“敢不阙疑，以俟能言者”。

然后二百年过去了……

祖氏父子继续搞这个东西，这次他们换了个方向，他们想去计算这牟合方盖与正方体差的那部分体积，这样也能求出牟合方盖的体积。

对于八分之一牟合方盖（就是特别像面包那个）：在高度 h 处作横截面，设截面积为 a²，如图：

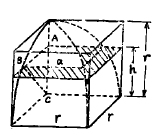
AB 是截面正方形的一条边，而 C 是八分之一牟合方盖的底边的一角（其实也是内切球的球心），三角形 ABC 是直角三角形。而 BC 边则是从圆心到圆周上的一条线（因为牟合方盖是被圆柱切出来的，图中的 BC 其实是半径为 r 的四分之一圆的一个半径），它的长度就是底边长度 r。

那么，由勾股定理，a²+h²=r²。

八分之一牟合方盖在高度 h 处的横截面积为 r²-h²，那么，八分之一正方形和八分之一牟合方盖差出的那么一个东西，在高度 h 处的横截面积就是 h²（图中阴影部分）。

而对于一个底面边长为 r，高也为 r 的倒置立方锥，其高度 h 处的横截面积正是 h²（很简单，可以自己证证看）。

这里，祖暅提出了祖暅原理，即：两个空间立体在同一高度处的截面积如果总是相同的，那么这两个空间立体等体积。

高度在 h 处的八分之一牟合方盖与八分之一正方体的截面面积差与立方锥截面面积居然是相等的。

也就是说，对于这么个八分之一牟合方盖，它与八分之一正方体的体积相比，刚好差出了一个同底等高的立方锥的体积。

高度为 r，底面边长为 r 的立方锥的体积很好算，是

那么八分之一牟合方盖的体积则是

牟合方盖的体积是

前面已经证明了牟合方盖的体积与内切圆的体积比是 4:π

那么，半径为 r 的球，即边长为 2r 的正方体的内切球的体积是

这就是祖氏父子得到球体体积公式的方法。

而微积分……还要再过一千年才发明出来……

参考文献

[1] 程向阳。中国球体积公式溯源

[2] 张伟。祖暅原理的由来及证明

本文图片来源：程向阳。中国球体积公式溯源