世界上有哪些代码量很少，但很牛逼很经典的算法或项目案例？

世界上有哪些代码量很少，但很牛逼很经典的算法或项目案例？

知乎精选

周巍青，珞珈山钉子户

快速傅里叶变换（FFT），核心算法用递归法几十行搞定。

计算机应用最为重要的算法之一，广泛应用于各种各样的工业和科学实践中。第一次看到递归算出快速傅里叶的时候，惊了很久。后来经过数学家的很多努力，有了新算法将复杂度从 N^2，降到 N*log(N)，觉得可以称之为人类智慧的精华了。

有空可以贴下源代码。

2020.1.15 这几天忙着科研，大家别急，今天一定抽空把算法和源代码贴出来。

第一次更新（1.15）：

众所周知，数学中有一个傅里叶变换，是将函数在实空间的定义域变换到倒空间的定义域上，这个变换非常重要，因为一些实空间不易发现的信息，在倒空间中会表现的非常明显，所以傅里叶变换是很多信号、物理的分析基础。它的形式如下：

以及其逆变换：

但是如果在计算机想要编程实现傅里叶变换就要不可避免地面临两个近似：第一，现实中我们无法将积分的上下界延伸到无穷，所以这里一定是一个有界积分；第二，无论什么连续的公式，只要是想要被计算机实现，就必须进行离散化，所以这里的连续积分（

）就近似为离散求和（

）。而基于这两种朴素近似下的，就是所谓的“离散傅里叶变换”（Discrete Fourier Transform，简称 DFT），它的形式也很直观：

看到这里，其实你如果利用 DFT 简单地编程，其实已经可以实现傅里叶变换了。但是我们为什么不用这个算法呢？是因为复杂度。

复杂度是算法中的一个概念，简单来说就是复杂度越高，那么这个算法计算大体系就越困难，那有多困难呢？我举个例子，现在算法基础库中对于矩阵的对角化应该是最基础和重要的了，矩阵的对角化的计算复杂度是

，就是说对角化的时间就随着矩阵维数的三次方增加，这是十分恐怖的增长。目前市面的通用的对角化库，比如 lapcak，对角化的极限维数一般也就在 10000, 这个量级。那 DFT 的复杂度是多少呢？你可以从公式上看到，如果你现在要对一个包含 N 个数的数组进行 DFT，那你每算其中一个变换后的数，都要进行 N 次的运算，那这个算法的复杂度也就是

，也就是说，用 DFT 最多也就只能处理大概一个拥有大概

个数的数组。但是在生产科研实践中，这实在不是一个大的上限，所以这个复杂度的硬伤一直制约着 DFT 的发展，而这就是属于当时制约整个人类文明进步的“卡脖子”的难题，如果 FFT 没有出现，那我们的世界现在绝对不是现在这个样子。

时间来到 1965 年，James Cooley 和 John Tukey 发现了一种算法，这种的算法的复杂度降低为了

，而这种算法就称之为“快速傅里叶变换”（Fast Fourier transform， 简称 FFT）。但其实，就这个问题，Danielson 和 Lanczos 在 1942 年就已经开始了相关的讨论。他们发现任何一个 DFT 其实可以重新改写成两个 DFT 的和：

数学家进一步发现这一分为二的 DFT 组，一个是原来是偶数项（even，第 0,2,4,6...项）组成的，而另一个是由原来的奇数项（odd）组成的。如果你只是看到这一步，你已经发现了一个大事情，就是原来用这个公式来算的话，求一个傅里叶变换不再需要进行 N 次相乘，而只需要 odd 组的 N/2 次运算，even 组的直接不用做任何运算直接拉下来就好了。那这样计算量不就减少一半了吗？但是其实事情并没有那么简单，我们刚才证明了任何一个 DFT 组都能被一分为二，而且计算量减半。但是我们现在一分为二得到的 even 组和 odd 组，他们不又是 DFT 组吗？我们可以继续之前的操作，将他们分别再次分为两个数组的求和！

Fig.1 DFT 的细分过程

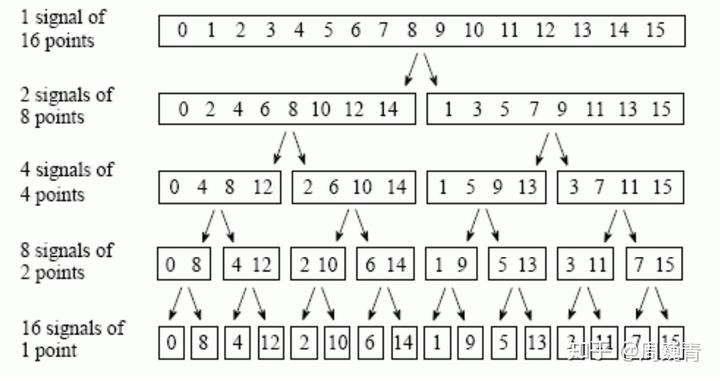
一分为二，二分为四，四分为八，一直分到每个数组只剩一个数字为止！而且每进行一次操作，就能使得其中一半的计算量被减少。这样我们就把计算量从

降到了

。你可能现在对这个算法的突破性还没有概念，我现在来给你构建下概念，

随着 N 的增加，FFT 算法对于 DFT 的优势会不断显现，一开始 1024 个数，FFT 比 DFT 快 100 倍；32768 个数，就快了 2000 多倍，到了我们之前提到的极限 1 百万个数，快了近 5 万倍！FFT 将我们的计算分析能力成万倍的提升。提一句，现在 FFT 最稳定最快的库是 FFTW，这个 W 是“in West”，就是说“西方的 FFT”。我当时刚看懂 FFT 时，不服气，一心想写个东方版，FFTE（FFT in East），后来和我自己的程序和 FFTW 性能一比，我人都傻了，果然好的 FFT 程序还是超级难写的。

这个算法关键的关键就是将 DFT 组不断奇偶细分，细分到最后时，如何确定每个数组前面的相位系数。我希望今天可以在第二次更新中把如何确定细分后的序列，以及蝶形算法更完。

Fig.2 蝶形算法

我先把我当时研一第一次接触到 FFT 编写的 Fortran 源码贴出来吧。短短几十行，如果你能花几天的时间理解这个递归程序，那么这将是 2020 年获得的第一个受益终身的知识。

2023.2.19 感谢评论区的建议，将

改为

。

! Cooley-Tukey FFT
recursive subroutine fft(x,sgn)

    implicit none
    integer, intent(in) :: sgn
    complex(8), dimension(:), intent(inout) :: x
    complex(8) :: t
    integer :: N
    integer :: i
    complex(8), dimension(:), allocatable :: even, odd

    N=size(x)

    if(N .le. 1) return

    allocate(odd((N+1)/2))
    allocate(even(N/2))

    ! divide
    odd =x(1:N:2)
    even=x(2:N:2)

    ! conquer
    call fft(odd, sgn)
    call fft(even, sgn)

    ! combine
    do i=1,N/2
        t=exp(cmplx(0.0d0,sgn*2.0d0*pi*(i-1)/N))*even(i)
        x(i)     = odd(i) + t
        x(i+N/2) = odd(i) - t
    end do

    deallocate(odd)
    deallocate(even)

end subroutine fft
查看知乎讨论