之前回答过这个问题，我搬运一下。以下方法可以找到一大批这种分数：

---

不久前看到知乎上有这样一个问题，题目来自于一张网络搞笑图：

此图要点在于，163/326 这个分数，经过不正确的约分方式，得到了正确的计算结果。题主就问，如何寻找到这样的，可以经过错误约分，得到正确结果的数字？其中排除像

这种平凡的结果。我把这种数字命名为“可错约数”。

因为“错约”的可能情形非常多，所以先把问题限定为分子分母等长，且约分后，分子为 1 的情况。很快，有人通过计算机，找到了很多这样的数：

一些 3 位“可错约数”：

一些 4 位可错约数：

看上去没啥规律。但我想起之前有关“走马灯数”的文章中，提到一种技巧，可以批量寻找这种“可错约数”。比如，因为分子分母等长，且约分后，结果为 1/n，则分子、分母似乎可以满足以下竖式：

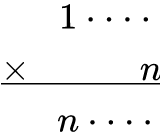
那么以上竖式中，如果省略号部分的数字恰好可约，那么被乘数和积可组成一个“可错约数”。省略号部分可能的组合非常多，不过似乎最简单的一种是这种组合：

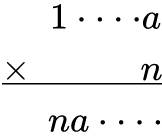
其中 a 是 1-9 的某个数字，其余省略号部分完全相等。这种形式的乘积与“走马灯”数很类似，因此可以考虑如下循环小数的乘积形式：

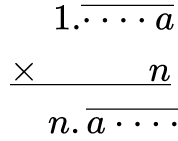
设上式的乘积结果为 x，则

，所以

为被乘数。

综合以上就有：

可解得：

可见

的循环节就是以上的竖式中的循环节。所以只要取 n 和 a 代入:

展开得到循环节，即可生成可错约数。

例如希望结果为 1/2，则 n=2，公式为:

当 a=1 时：

， 循环节最左边添加 2，得到分母：2105263157894736842，分母除以 2 得到分子：1052631578947368421，最终分数为：

a 取其他值一样可以，比如 a=9，

， 则可以得到：

n 取 1 到 9 都可以，比如 n=5, a=3 时：

， 则可以得到：

以上方法稍微改动下就可以有很多变体的解，欢迎发在评论区。